前言:写这玩意是真费手啊!!![]()
T1 增加模数
-
题目大意:给定H对(Ai,Bi)和 M。计算(A1^B1+A2^B2+…+AH^BH)mod M的值。
-
大体思路:根据时间限制和数据范围初步判断,可以快速幂直接计算。这里需要注意单独考虑A=0&&B=0的情况 。不知道不开long long会不会见祖宗,反正开了肯定错不了!

-
核心代码(快速幂函数):
long long r=1%m;
a=a%m;
while(b>0){
if(b%2==1) r=(r*a)%m;
a=(a*a)%m;
b=b/2;
}
return r;
T2 人工降雨:
-
题目大意:
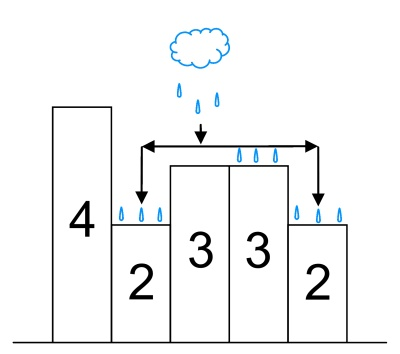
如果一个位置能被雨淋到,而且紧挨着的旁边的建筑不高于他,那么旁边的建筑也能被雨淋到。问最多能淋到雨的位置有几个。 -
大体思路:看这个1e3的数据量,直接暴力水过去就行了。遍历每个点,循环模拟一下,看最多能淋到几个建筑。最后取个max。看到这题我的第一反应竟然是最长上升子序列!现在想一想当一定是疯了。。。。。。
-
核心代码:
for(int i=0;i<n;i++) {
int sum=1;
for(int j=i-1;j>=0;j--) {
if (h[j]<=h[j+1]) sum++;
else break;
}//向左遍历
for (int j=i+1;j<n;j++) {
if(h[j]<=h[j-1]) sum++;
else break;
}//向右遍历
if(sum>Max) Max=sum;//记录最大值
}
T3 Static Range Minimum Queries:
-
题目大意:
给定一个由n个整数组成的数组,你的任务是处理q个查询,查询形式为:在范围[a,b]中的最小值是多少? -
大体思路:对于这个问题,我们需要高效处理大量区间最小值查询(RMQ)。考虑到数据范围(n和q都可能达到2×10^5),我们需要使用时间复杂度为O(n log n)预处理和O(1)每查询的算法,不出意外的话应该是ST表。
-
核心代码:
void ST() {
for(int i=0;i<n;i++) b[i][0]=a[i];
for(int j=1;(1<<j)<=n;j++) for(int i=0;i+(1<<j)-1<n;i++) b[i][j]=min(b[i][j-1],b[i+(1<<(j-1))][j-1]);
}//ST表,我就不多说什么了
T4 Meet in the Middle:
-
题目大意:
给定 n 和一个长度为 n 的数组,有多少种方法选择一个该数组的子集使得和为 x 。 -
大体思路:双向搜索模板题。
将数组分成两半,对前一半进行搜索并存储结果,然后搜索后一半并计算前一半中与其匹配的结果总数。 -
核心代码:
void s1(const vector<int>& nums,int start,int end,vector<long long>& sums,long long sum1=0) {
if (start > end) {
sums.push_back(sum1);
return;
}
s1(nums,start+1,end,sums,sum1+nums[start]);
s1(nums,start+1,end,sums,sum1);
}
long long s2(const vector<int>&nums,int x){
int n = nums.size();
int mid = n / 2;
vector<long long>sum2, sum3;
s1(nums,0,mid-1,sum2);
s1(nums,mid,n-1,sum3);
unordered_map<long long, long long> R;
for (long long sum : sum3) R[sum]++;
long long count = 0;
for (long long sum : sum2){
long long y=x-sum;
if (R.find(y)!=R.end()) count+=R[y];
}
return count;
}
T5 Bovine Genomics:
-
题目大意:
奶牛的斑点不仅可以通过基因组中的一个或两个位置解释,还可以通过观察三个不同的位置集合来解释。请帮助他计算能够解释斑点的三个不同位置集合的数量。 -
大体思路:
这个问题要求我们找出所有可能的三元位置组合(i,j,k),使得在这些位置上,斑点奶牛和无斑点奶牛的基因序列没有重叠。也就是说,对于任何斑点奶牛和无斑点奶牛,它们在这三个位置上的基因组合应该是不同的。 -
核心代码:
for (const string &p : pl) {
string key;
key += p[i];
key += p[j];
key += p[k];
if (spz.count(key)) {
valid = false;
break;
}
//枚举三种基因的排列情况
}
if (valid) ++count;//符合题目要求,总数加一
T6 盛宴:
-
题目大意:
找出满足条件的连续食材区间,使得:
• 总香味值 ≥ M;
• 在所有满足条件的方案中,最大辣度尽可能小。 -
大体思路:
先二分查找,用来确定最小的尺寸上限,通过不断缩小范围来找到最优解。滑动窗口用来判断在给定的尺寸上限下,是否存在一种合法的方案,使得总费用不超过 m。 -
核心代码:
while (sum >= M) {
ll max_S = S[q.front()];
if (max_S < min_max_S) {
min_max_S = max_S;
}
sum -= F[left];
if (q.front() == left) {
q.pop_front();
}
left++;
}
T8 邦布照相:
-
题目大意:
给定平面上N个点,找出其中的一对点的距离,使得在这N个点的所有点的对中,该距离为所有点对中最小的。(2<=n<50000) -
大体思路:
遍历邦布型号的序列 ,我们对于这个 x 中的每个元素都检查一下他在不在栈里已经出现过,如果出现过的话就直接跳过这个元素进入下一个元素。
还有为了保证答案字典序最小,我们如果当前这个元素大于栈顶的元素的时候,我们就把栈顶元素弹出然后把哈希表里的这个元素也要移除。最后输出。 -
核心代码:
for(int i=0;i<n;i++){
if(该元素已经被加入){
跳过
}
while(如果当前元素小于栈顶并且后面还会出现栈顶所代表的元素){
删除栈顶,删除哈希表中所代表的元素
}
元素入栈,存入哈希表
}