智灵普及+班模考总结
当前编写状态:
T1
T2
T3
T4
T5
T6
T7
T8
全部完成!
T1
思路:使用快速幂计算出每组幂,再分别 modM ,最后输出即可
some code:
//快速幂函数
int p_m(int a,int b,int mod){
a%=mod;
if(a==0)return 0;
int res=1;
while(b>0){
if(b&1){
res=(res*a)%mod;
}
a=(a*a)%mod;
b>>=1;
}
return res;
}
T2
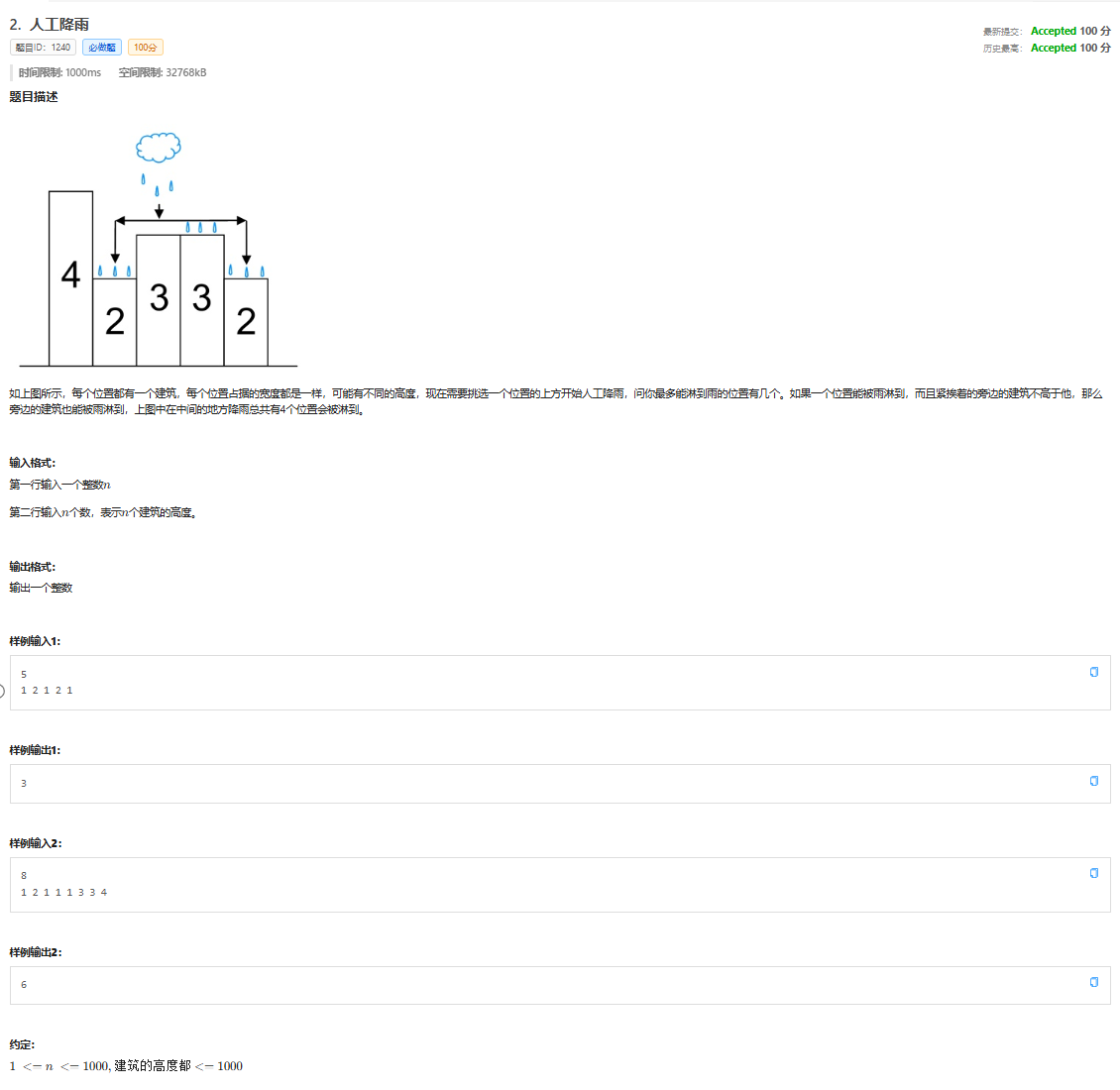
思路:用深搜,枚举一遍所有屋顶上降雨的情况,即判断左右两边房顶的高度,检查是否可以流过去,并计数
我这里把向左搜索,向右搜索合并到一个函数了,所以要用一个vis防止反复搜索。其实也可以把两个分开写,这样就不用vis了
some code:
void dfs(int wz/*当前位置*/,int last/*上个位置*/){
if(vis[wz]) return;
if(wz<0||wz>=n) return;
if(a[wz]>a[last]) return;
ans++;
vis[wz]=1;//标记,防止两个高度相同的屋子相互回流
dfs(wz+1,wz);
dfs(wz-1,wz);
vis[wz]=0;
}
(其实,这题还可以用单调栈)
T3
思路:首先想到使用暴力:输入边界后暴力枚举每个点的值,求 min 即可
50tps code
#include<bits/stdc++.h>
using namespace std;
int n;
int a[200005];
int main(){
int T;
cin>>n>>T;
for(int i=0;i<n;i++) cin>>a[i];
while(T--){
int x,y;
cin>>x>>y;
x--,y--;
int ans=1e9;
for(int i=x;i<=y;i++){
ans=min(ans,a[i]);
}
cout<<ans<<endl;
}
return 0;
}
然后,考虑构建稀疏表(ps:其实这题不用稀疏表也可以),构建表后通过查询两个可能重叠的区间的最小值,判断查询区间的最小值。
some code:
int st[200005][20];//构建稀疏表
for(int i=0;i<n;i++) st[i][0]=a[i];
for(int j=1;j<20;j++) {
for(int i=0;i+(1<<j)<=n;i++) {
st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]);
}
}
T4
思路:从这名字就看得出来,这是一道典型的折半深搜题板子题(ps:直译怎么是中间相遇)。首先考虑使用单向深搜,果不其然TLE了。
再考虑使用折半深搜,使用两个dfs,分别搜索数组的一半,改一下边界条件即可
some code:
void dfs(int xx,int sz){
if(sz>x||xx>n) return;
if(sz==x){
ans++;
return;
}
dfs(xx+1,sz+a[xx]);
dfs(xx+1,sz);
}
T5
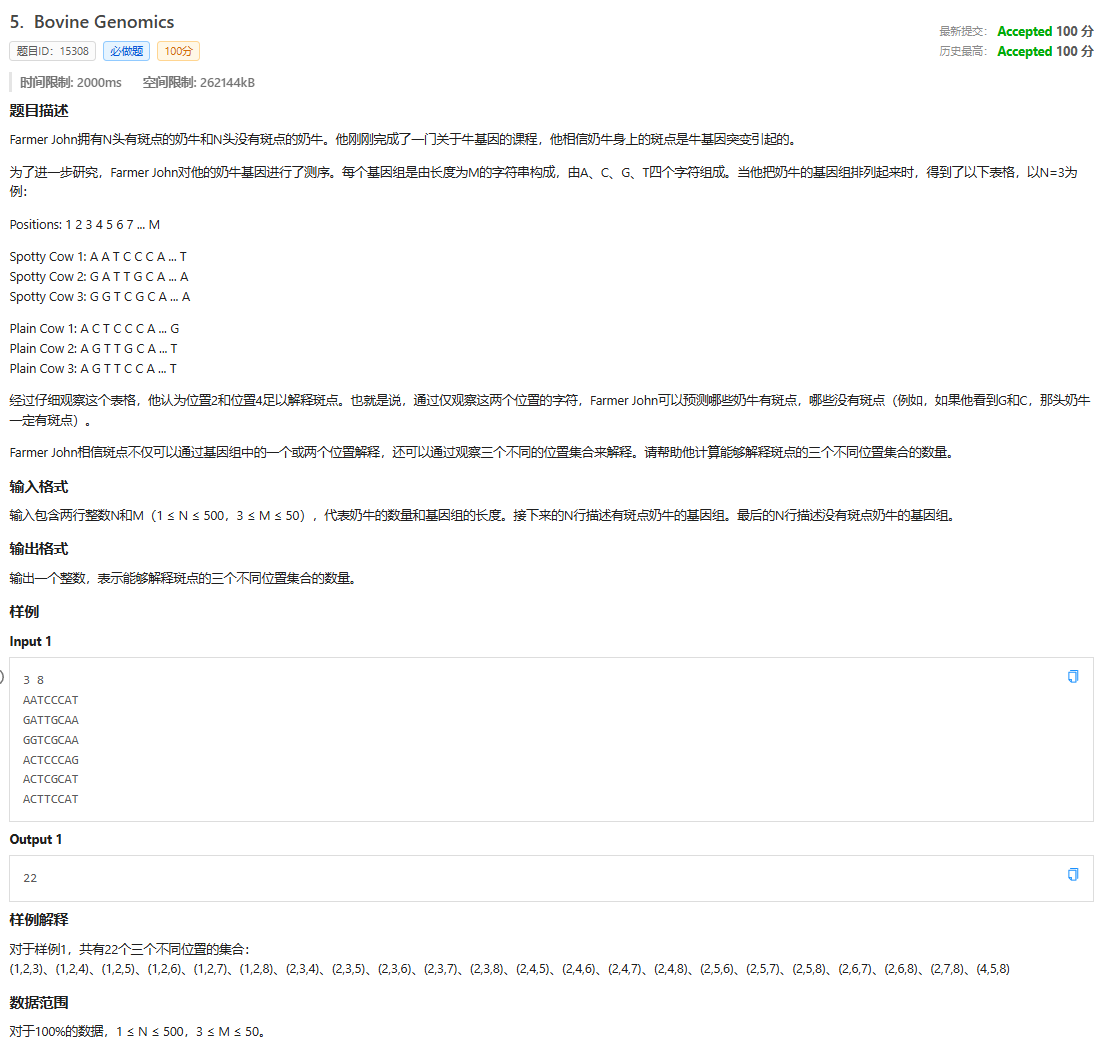
思路:考虑暴力枚举+标记,计算在斑点牛与普通牛中有多少组三个位置 (i,j,k) 的组合满足:
在所有斑点牛在这三个位置的基因组合不会出现在任何普通牛的对应位置组合中。
最后输出答案即可
some code:
//前面枚举三种基因的排列情况
for(const string&s:spotty){
int c1=change[s[i]];
int c2=change[s[j]];
int c3=change[s[k]];
int code=(c1<<4)|(c2<<2)|c3;
spotted[code]=true;
}
bool valid=true;
for(const string&p:plain){
int c1=change[p[i]];
int c2=change[p[j]];
int c3=change[p[k]];
int code=(c1<<4)|(c2<<2)|c3;
if(spotted[code]){
valid=false;
break;
}
}
T6
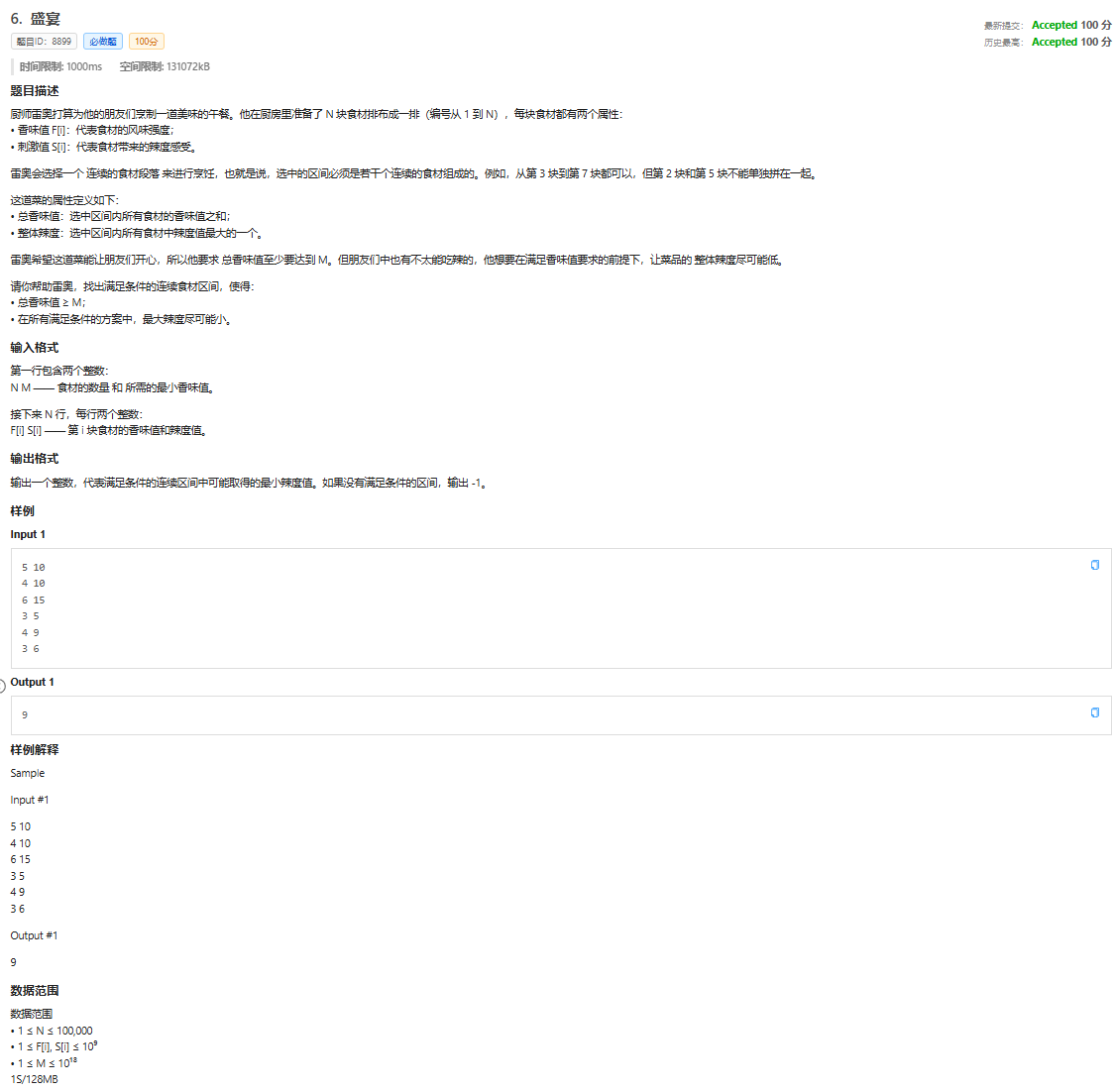
首先考虑使用暴力:枚举所有可能的连续区间,对于每个区间,计算香味值之和和最大辣度。
在所有满足香味值之和 ≥ M 的区间中,记录最小的辣度和。
但是,时间复杂度…也就是高了这么亿点点。。。
正解有三种方法,让我为你一一呈上:
1.滑动窗口+单调队列优化
我们需要找到一个窗口 [l, r] 使得香味值之和 ≥ M ,同时窗口内的最大辣度尽可能小。
由于香味值之和需要 ≥ M ,我们可以固定左边界 l ,找到最小的 r 使得香味值之和 ≥ M ,然后记录此时的最大辣度。
为了提高效率,可以使用单调队列优化(维护一个递减的队列,队首是当前窗口的最大值)。
【我的方法】2.二分答案+滑动窗口
我使用的就是这种方法
滑动窗口都没用怎么办
二分可能的辣度值 S ,检查是否存在一个区间,其最大辣度 \le S 且香味值之和 ≥ M 。
对于二分的某个辣度值 S ,我们需要检查是否存在一个连续区间,其中所有食材的辣度 ≤ S ,且香味值之和 ≥ M 。
some code:
bool check(int mid){
int sum=0;
for(int i=0;i<n;i++){
if(s[i]>mid) sum=0;
else{
sum+=f[i];
if(sum>=m) return true;
}
}
return false;
}
3.双指针+稀疏表
其实就是比方法1多了一个使用稀疏表预处理实现 O(1) 的查询时间复杂度
具体地:
固定左指针 l ,移动右指针 $r ,直到香味值之和 ≥ M 。
记录当前窗口的最大辣度(可以用稀疏表预处理, O(1) 查询)。
然后移动左指针 l ,继续寻找下一个可能的窗口。
其实,还可以用线段树预处理,也可以实现 O(1) 复杂度的查询。但是,显然,这种难度不太适合我这种蒟蒻使用
T7
题面
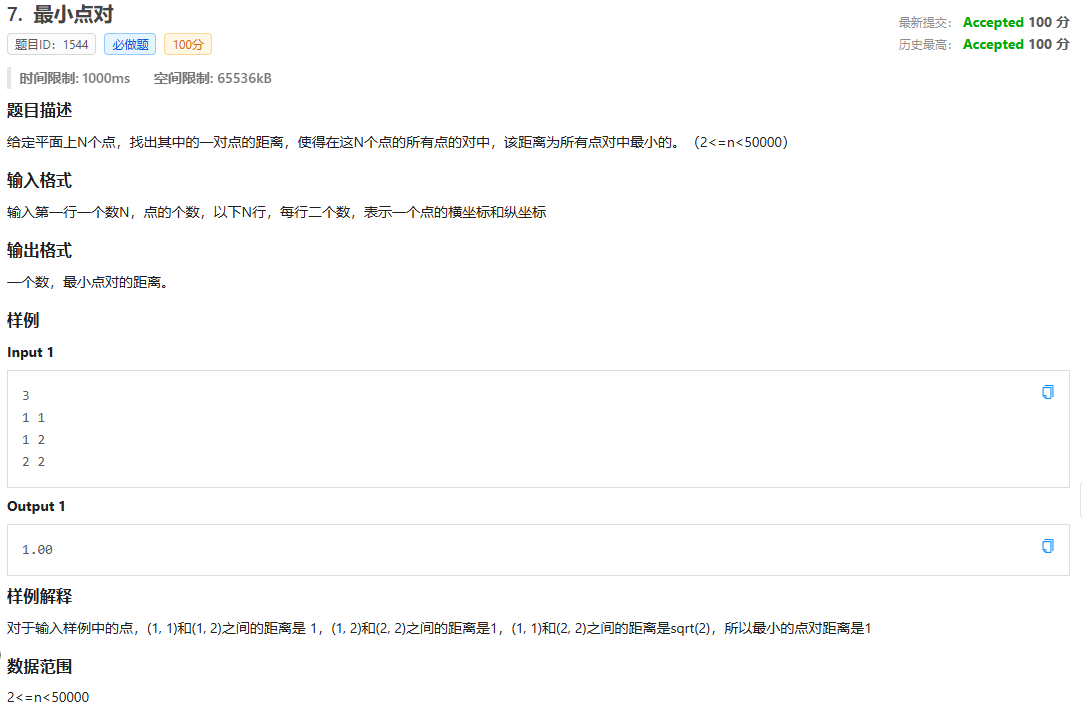
思路:考虑暴力枚举所有点的坐标,计算距离,取最小值即可
这题很坑的一点:输入的坐标可能为小数!!!
再回到暴力的思路上:
暴力计算时间复杂度会超,所以考虑使用分治法求解平面最近点对
步骤:
1.递归分割:
按 x 坐标排序后,将点集分为左右两半。
分别递归计算左右半部分的最小距离平方 dLeft 和 dRight。
取较小者 d = min(dLeft, dRight)。
2.处理中间带:
收集所有与中线 x 坐标距离不超过 sqrt(d) 的点(通过比较平方优化)。
按 y 坐标排序后,检查每个点与其后最多 6 个点的距离(利用几何性质减少计算)。
3.合并结果:
返回 min(中间带最小距离, d)。
some code:
double ff(vector<node>&a,int l,int r){
if(r-l+1<=3){
return bruteForce(a,l,r);
}
int mid=(l+r)/2;
node midnode=a[mid];
double dLeft=ff(a,l,mid);
double dRight=ff(a,mid+1,r);
double d=min(dLeft,dRight);
vector<node>b;
for(int i=l;i<=r;++i){
double dx=a[i].x-midnode.x;
if(dx*dx<=d){
b.push_back(a[i]);
}
}
sort(b.begin(),b.end(),cmpy);
double minn=d;
for(int i=0;i<b.size();++i){
for(int j=i+1;j<b.size()&&j<=i+6;++j){
if(jl(b[i],b[j])<minn){
minn=jl(b[i],b[j]);
}
}
}
return min(minn,d);
}
T8
题面
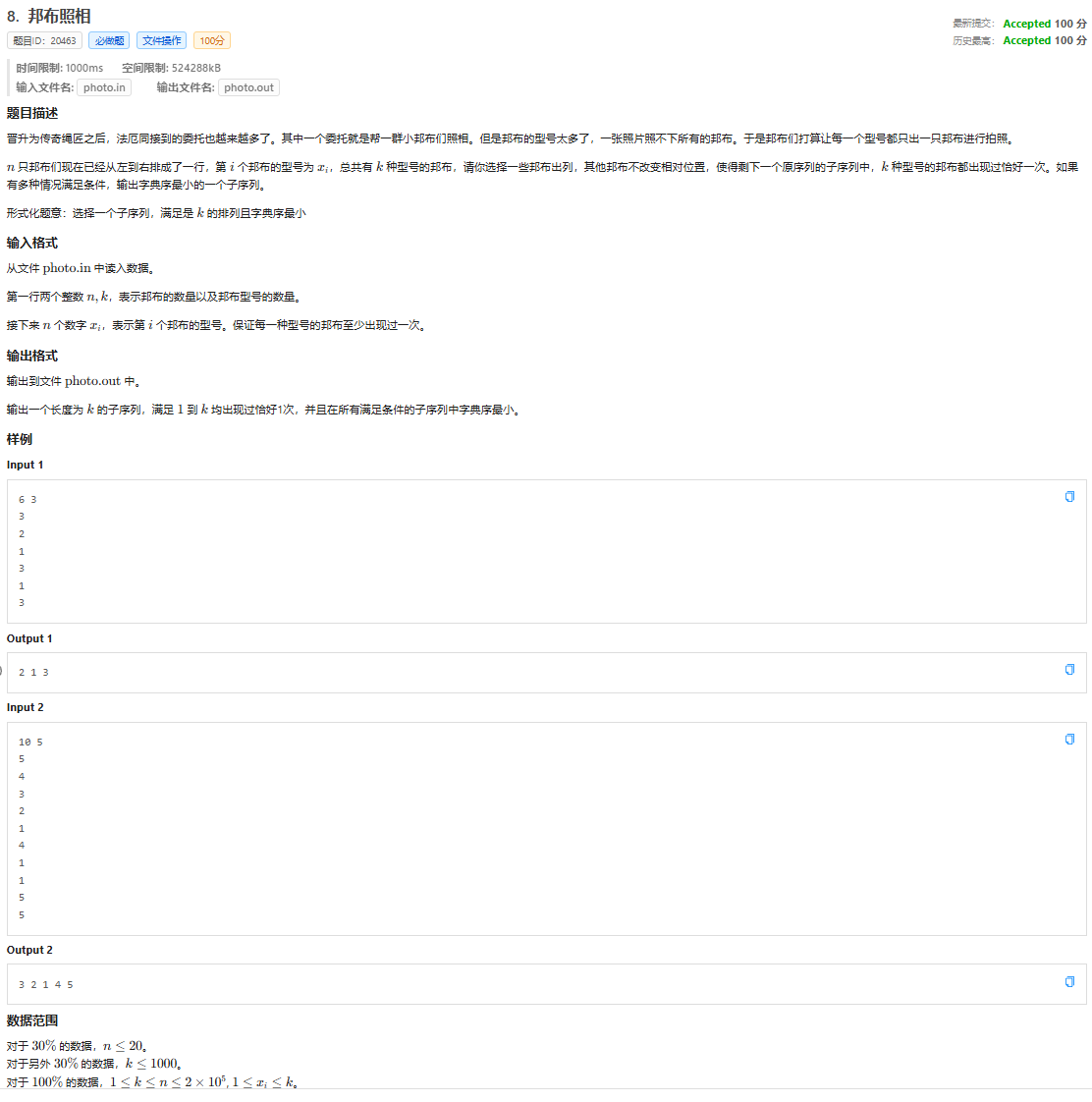
提示:这题不要忘了文件读写
思路:考虑预处理数的最后出现位置,通过贪心构建最小字典序子序列。其实这题比前面几题比起来还算简单,就是文件读写突然冒出来一个有点坑人
some code:
for(int i=0;i<n;++i){
int x=a[i];
if(used[x])continue;
while(!stack.empty()){
int top=stack.back();
if(x<top&&last_occurrence[top]>i){
used[top]=false;
stack.pop_back();
}else{
break;
}
}
stack.push_back(x);
used[x]=true;
if(stack.size()==k)break;
}
\Huge 完
点 个 赞 吧