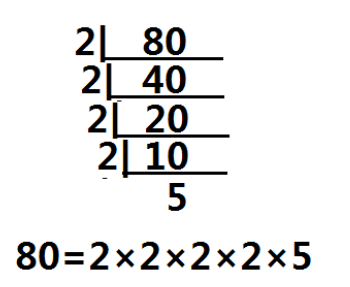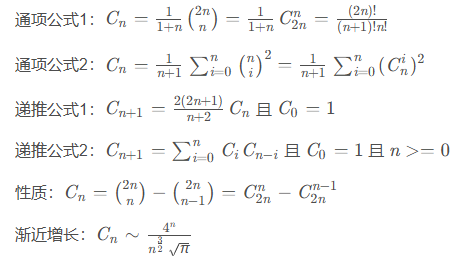0. 前言
在这个帖子里,我将整理CSP-J(包括一点CSP-S)的初赛部分知识点。
1. 初赛的题目结构
初赛题目分三个大模块:
-
选择题(15道题目,每题4个选项,每题2分,共30分)
-
阅读程序题(共三道大题,每题分判断题与选择题,基本上是判断题每题1.5分,选择题每题3分,三道大题共40分)
-
完善程序题(共两道大题,每道大题5个空,每空3分,共30分)
2. 信息学基本常识
一般来说,信息学基本常识是必考知识点,但是考试中只会出现在选择题一类,一般占4~8分。
2.1 信息学及计算机史
2.1.1 计算机奖项
一般来说,考试会考到这两种奖项:
- 图灵奖:由美国计算机协会创造(简称ACM),设立于1966年,也被称为计算机界的诺贝尔奖。
- 冯·诺依曼奖:目的是表扬在计算机科学和技术上具有杰出成就的科学家。
这两个奖都是以人的名字命名,而他们两个也都是大神(蒟蒻高攀不起)
2.1.2 世界上第一台电子计算机
世界上第一台电子计算机于1946年的2月14日在美国美国宾夕法尼亚大学诞生,名为 ENIAC 。
2.1.3 例题
例题
1.【CSP-J 2019】 以下哪个奖项是计算机科学领域的最高奖?
A.图灵奖
B.鲁班奖
C.诺贝尔奖
D.普利策奖
2.【CSP-J 2021】 以下奖项与计算机领域最相关的是( )。
A.奥斯卡奖
B.图灵奖
C.诺贝尔奖
D.普利策奖
3. 世界上第一台电子计算机的名字叫( )。
A. EINAC
B. EIANC
C. ENIAC
D. ENACI
答案
A
B
C
2.2 关于编程
2.2.1 编程语言
编程语言包括两类,面相对象与面向过程。
2.2.2 高级语言与低级语言
常见的低级语言:汇编
面向对象的高级语言:C++、Java等
面相过程的高级语言:C、Fortran等
2.2.3 例题
例题
1.【CSP-J 2021】 以下不属于面向对象程序设计语言的是( )。
A.C++
B.Python
C.Java
D.C
答案
D
2.3 关于计算机
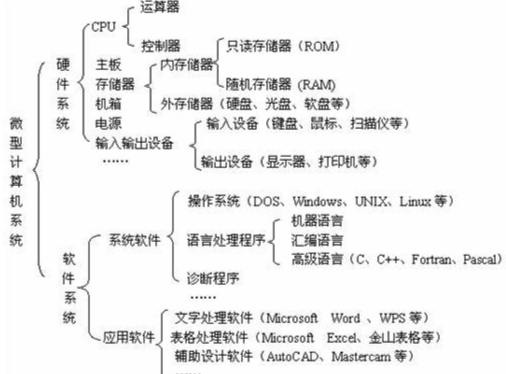
2.3.1 CPU、运算器、存储器
中央处理器(也叫CPU)=运算器+控制器+寄存器
存储器=外存储器+内存储器
运算器=算术逻辑运算单元+浮点运算单元
2.3.2 【常考】断电后的数据保存
断电后可以保存数据:硬盘,ROM
断电后不可以保存数据:显存(显卡内存),RAM,CPU
(有的时候我也不知道,为什么出题组这么闲,谁会无聊试)这个啊)
2.3.3 计算机的存储单位和关系
计算机的存储单位:
TB GB MB KB B bit
除了bit,他们的进位关系是1024:就像苹果手机,512GB的内存下一级就是1TB了,其实也可以说成1024GB。
bit的是比较特殊的,1B=8bit。
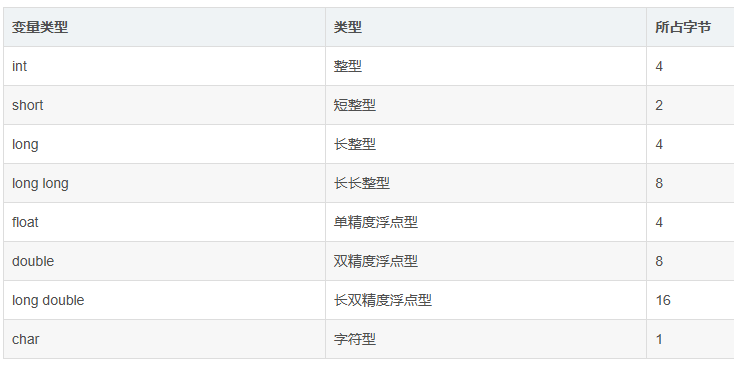
还有这个表格,背下来就好了:
2.3.4 ASCII码
附:ASCII码
ASCII码的正规名称是:美国信息交换标准代码,是基于拉丁字母的一套电脑编码系统。是最通用的信息交换标准。一共定义了128个字符。
几种比较常用的转换:
字符0→48
大写字母A→65
小写字母a→97
初赛、复赛都能用!
2.3.5 例题
例题
1.【CSP-J 2019】一个 32 位整型变量占用()个字节。
A. 32
B. 128
C. 4
D. 8
2.【CSP-J 2023】 在计算机中,以下哪个选项描述的数据存储容量最小()
A.字节 (byte)
B.比特 (bit)
C.字 (word)
D.千字节 (kilobyte)
3. 断电后可以保存数据的是( )。
A. 显存
B. RAM
C. ROM
D. CPU
答案
C
B
C
3.进制
进制,一般来说我们只考这几种进制:十进制、二进制、八进制、十六进制。
3.1 二进制与其相关知识
计算机使用的都是二进制。
对于二进制的相关知识,这篇帖子里并没有介绍那么完整。
对于想看位运算的同学们,建议查看c++位运算讲解 的位运算帖子。
3.1.1 原码、反码、补码
这就是二进制的基础知识。
- 1.原码
原码就是十进制数转换成二进制后形成的二进制编码。 - 2.补码
正数的补码是其本身,而负数的补码是其反码的值加上1。 - 3.反码
正数的反码是其本身,负数的反码是其除符号位之外的所有位按位取反的结果。
3.1.2 位运算
位运算吗,还是建议去看上面的那个帖子的。
这里只讲一些轻微的小位运算。
首先,初赛常考的位运算有这几种:按位与(& 或 ∧) 、按位或(| 或 ∨)、位移运算(<<和>>)、按位取反(~)、按位异或(^)。
注意:异或的符号和逻辑与的符号是有差别的。
逻辑表达式 是逻辑非(!或 ┐)、逻辑与(&& 或 ∧) 、逻辑或(|| 或 ∨)组成的表达式,结果只有0、1,也就是结果 true 、 false 。
其他的运算
我认为这些运算应该各位都会吧:
>=、<=、==、!=
3.1.3 例题
例题
1.【CSP-J 2021】 目前主流的计算机储存数据最终都是转换成( )数据进行储存。
A.二进制
B.十进制
C.八进制
D.十六进制
2.看代码说结果:( )
#include
using namespace std;
int f(int x){
return x&-x;
}
int main(){
int a[5]={4,10,19,22,89},sum=0;
for(int i=0;i<5;i++)
sum+=f(a[i]);
cout<<sum;
return 0;
}
A.8
B.10
C.18
D.20
3. 设 x=true,y=true,z=false,以下逻辑运算表达式值为真的是( )。
A.(y∨z)∧x∧z
B.x∧(z∨y) ∧z
C.(x∧y) ∧z
D.(x∧y)∨(z∨x)
答案
A
B
D
3.2 进制转换
3.2.1 十进制转N进制
首先。我们需要知道一种除法,名为“短除法”。
道理也很简单,请看下面这个图片:
这是一个短除法分解质因数的问题。
可以看到,最上方的是被除数,左边是除数,下边是商,随后,商变为被除数,以此类推。
而十进制转N进制就是要采用这种方法。
在除法时,我们的余数写在右边。
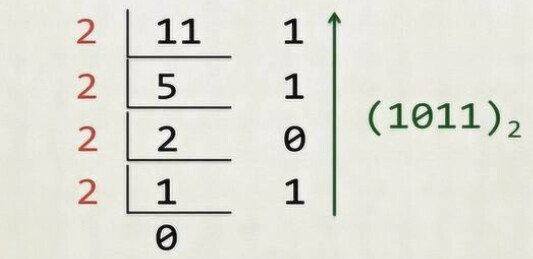
如:将十进制数11转换为二进制数:
利用短除法,计算余数,最后倒着写,就完成啦!
(简单ing)
大家也可以自己举例尝试。
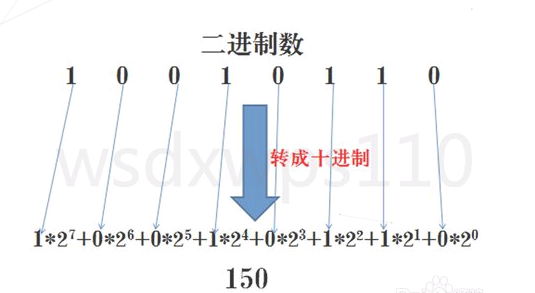
3.2.2 N进制转十进制
个人认为这个简单一点。
简单说就是:倒着转换,第一位是 N^0,第二位是 N^1…以此类推。
看图:
3.2.3 小数的转换
十进制转任意进制的小数不进行除法运算,而进行乘法运算后取整,取整后从前向后排列。
任意进制转十进制的小数只需要乘上负指数,最后算出来即可。
3.2.4 进制求和
两个非十进制的数怎么求和呢?
先按照普通的竖式计算,但是满N进位,不是满十进位。
3.2.5 例题
例题
1.【CSP-J 2020】二进制数 1011 转换成十进制数是( )。
A. 11
B. 10
C. 13
D. 12
2.【CSP-J 2021】 二进制数 101.11 对应的十进制数是( )。
A. 6.5
B. 5.5
C. 5.75
D. 5.25
3. 【CSP-J 2023】八进制数12345670和07654321的和是( )。
A.22222221(8)
B.21111111 (8)
C.22111111(8)
D.22222211(8)
提示:后面的(8)是八进制的意思,(2)就是二进制。
4.【CSP-J 2023】数101010(2)和166(8)的和为( )。
A.10110000 (2)
B.236 (8)
C.158
D.A0(16)
答案
A
C
D
D
3.3 各进制的字母表达
H(Hexadecimal)——16进制
D(Decimal)——10进制
O(Octonary)——8进制
B(Binary)——2进制
4.图论、树论理论知识
这是一个困扰我的专题。
4.1 图、树基本概念
-
完全图:任意两点都有边相连,我们很容易推出来,一张完全图的边数为 n×(n-1)/2 。
-
连通图:顾名思义,连通图就是连通的图,即任意两点都能直接或间接到达,这就区别于完全图必须直接用边到达的定义。
-
树:任意两点之间的简单路径有且只有一条。树是一棵连通且无环的图,边数是n−1。
-
二叉树:每个节点最多只有两个子节点。
-
完全二叉树:只有最后一层不是满的,且最后一层的所有节点均集中在左侧。
-
满二叉树:节点个数已满。
4.2 遍历树、图
有这三种遍历方式:
- 先序遍历:遍历方式如下:根—>左儿子—>右儿子
- 中序遍历:遍历方式如下:左儿子—>根—>右儿子
- 后序遍历:遍历方式如下:左儿子—>右儿子—>根
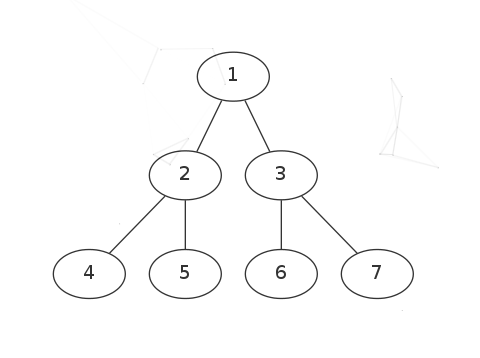
以二叉树为例:
先序遍历:1245367
中序遍历:4251637
后序遍历:4526731
4.3 例题
这个章节就是这么的快~
例题
1.【CSP-J 2019】假设一棵二叉树的后序遍历序列为 DGJHEBIFCA,中序遍历序列为 DBGEHJACIF,则其前序遍历序列为()。
A. ABCDEFGHIJ
B. ABDEGHJCFI
C. ABDEGJHCFI
D. ABDEGHJFIC
2.【CSP-J 2020】 有 10 个顶点的无向图至少应该有( )条边才能确保是一个连通图。
A. 9
B. 10
C. 11
D. 12
答案
B
A
5.数据结构理论知识
与上一章节对应。
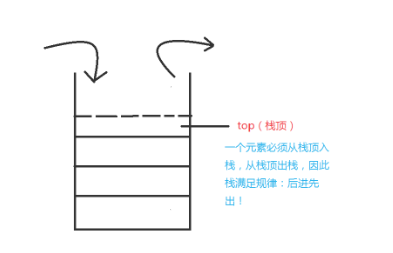
5.1 栈
先进后出、后进先出。
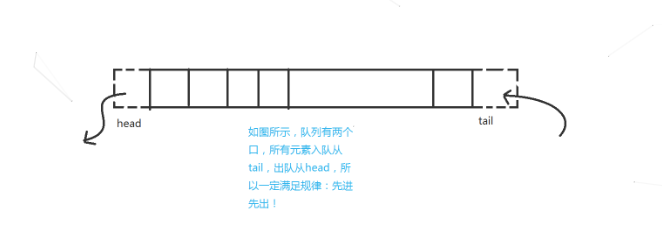
5.2 队列
先进先出、后进后出,像排队一样。
5.3 链表
链表有单向链表和双向链表,在这里不多说。
5.4 例题
例题
1.【CSP-J 2020】 链表不具有的特点是()。
A.可随机访问任一元素
B.不必事先估计存储空间
C.插入删除不需要移动元素
D.所需空间与线性表长度成正比
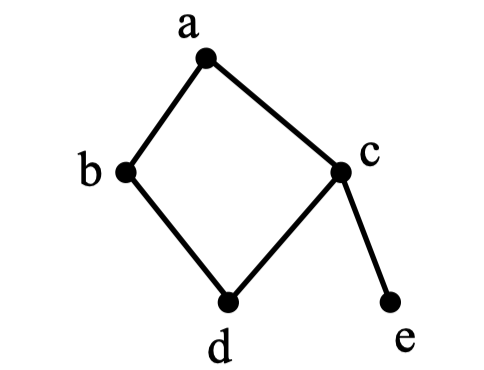
2.【CSP-J 2020】 下图中所使用的数据结构是( )。

A.栈
B.队列
C.二叉树
D.哈希表
3. 【CSP-J 2021】对于入栈顺序为 a,b,c,d,e 的序列,下列( )不是合法的出栈序列。
A. a,b,c,d,e
B. e,d,c,b,a
C. b,a,c,d,e
D. c,d,a,e,b
答案
A
A
D
6. 计算时间复杂度
一般来说,时间复杂度这么计算:
6.1 找出算法中的基本语句
算法中执行次数最多的那条语句就是基本语句,通常是最内层循环的循环体。
6.2 计算基本语句的执行次数的数量级
只需计算基本语句执行次数的数量级,这就意味着只要保证基本语句执行次数的函数中的最高次幂正确即可,可以忽略所有低次幂和最高次幂的系数。这样能够简化算法分析,并且使注意力集中在最重要的一点上:增长率。
6.3 用大Ο记号表示算法的时间性能
将基本语句执行次数的数量级放入大Ο记号中。
7. 排列组合
排列组合是每年必考知识点。但是这是一个比较大的课题。不仅是高二数学选修重点,也是数学编程的一个重要分支。
从某博客上截得,这玩意太难写了…
8.前缀、后缀、中缀表达式
这一章节需要用到栈的知识。
8.1 中缀表达式
像1+1,2+(5-3),a×b+c/d-e这种表达式都是中缀表达式,也就是我们最常用的一类。
特点:需要用到小括号
表达方式:值1 符号 值2
8.2 前缀表达式与后缀表达式
这两种表达式恰好相反。
a×b+c/d-e这个式子:
后缀表达式这样写:a b × c d / + e -
前缀表达式恰好相反。
写法就是先找到小括号,然后写出,如(a+b),后缀是a b +,前缀是 + a b。
然后是乘除法,道理一样,最后加减。
特点:不用小括号就可以写出。
表达方式:
前缀:符号 值1 值2
后缀:值1 值2 符号
8.3 例题
例题
【CSP-J 2021】表达式 a*(b+c)*d 的后缀表达式为( ),其中 * 和 + 是运算符。
A. **a+bcd
B. abc+*d*
C. abc+d**
D. *a*+bcd
答案
B
9.搜索(遍历)
有同学要问了:这初赛考吗?
别说,还真考过。
在 4.2 章时,我们讲过了遍历图、树。
这一章也差不多。
在 4.2 章 先序遍历就相当于深度优先搜索(遍历)。
而广度优先搜索(遍历)就是保存当前点能到达的所有点。
如二叉树:
深度优先搜索(遍历):1245367
广度优先搜索(遍历):1234567
例题
答案
B
10. 高精度加、减
对于仅仅想要过初赛的来说,这个章节可以废掉,去看阅读程序里讲了初赛的高精度。这里,我讲的是初赛、复赛融合的。
10.1 高精度加法
加法的计算方法是模拟竖式的方式。
10.1.1 第一步:存储
我们知道,一般高精度的范围非常大,1000位都是有的。
所以,long long 被pass,使用字符串存储是很好的方式。
char c[1005],c1[1005];
cin>>c;
cin>>c1;
int len1=strlen(c);
int len2=strlen(c1);
10.1.2 第二步:倒序
我们在加法的时候要使用倒序。
for(int i=0;i<len1;i++){
a[len1-1-i]=c[i]-48;
}
for(int i=0;i<len2;i++){
b[len2-1-i]=c1[i]-48;
}
将字符串倒序并将ASCII码转换,存储到int类型的数组里。
10.1.3 第三步:计算
我们按照以下的方式计算,直到算完为止:
d[len3]=a[len3]+b[len3]+r;
r=d[len3]/10;
d[len3]%=10;
len3++;
其中r是余数。
10.1.4 第四步:输出
while(d[len3]==0&&len3>0){
len3--;
}
for(int i=len3;i>=0;i--){
cout<<d[i];
}
10.2 高精度减法
根据高精度加法,来看看减法的思路:
#include <iostream>
#include <cstring>
using namespace std;
char a[6000],b[6000],c[6000];
int x[6000],y[6000],z[6000];
int main(){
cin>>a;
cin>>b;
if(strcmp(a,b)==0){
cout<<"0";
return 0;
}
int lena=strlen(a);
int lenb=strlen(b);
if(lena==lenb&&strcmp(a,b)<0||lenb>lena){//判断是否负数
strcpy(c,a);
strcpy(a,b);
strcpy(b,c);
swap(lena,lenb);
cout<<"-";
}
for(int i=0;i<lena;i++){
x[lena-1-i]=a[i]-48;
}
for(int i=0;i<lenb;i++){
y[lenb-1-i]=b[i]-48;
}
for(int i=0;i<lena;i++){
z[i]=x[i]-y[i];
if(z[i]<0){
z[i]=z[i]+10;
x[i+1]--;
}
}
while(z[lena-1]==0){
lena--;
}
for(int i=lena-1;i>=0;i--){
cout<<z[i];
}
return 0;
}
11. 奇特的数列
有很多数列很经典,初赛很容易考到。
11.1 斐波那契数列
斐波那契数列是由斐波那契创造出的数列,满足:
a[1]=1;
a[2]=1;
a[n]=a[n-1]+a[n-2];
这样的性质。
11.2 卡特兰数
卡特兰数是组合数学中一个常出现在各种计数问题中出现的数列。
满足:
11.3 等差数列
等差数列是指从第二项起,每一项与它的前一项的差等于同一个常数的一种数列,常用A、P表示。这个常数叫作等差数列的公差,公差常用d表示。
满足:
a[n]=a[1]+(n-1)×d;
的性质。
12. 阅读程序
终于来到阅读程序!
其实,阅读程序并没有什么如此big的方法,主要就是模拟,找到程序在干什么,然后来推演。
一些小技巧:
在写判断题时,常常有那些对立面的题目,如【CSP-J 2022】的阅读程序第一题,判断题的最后三空:
程序总是输出一个整数 0。
当输入为 2 2 时,输出为 10。
当输入为 2 2 时,输出为 59。
很明显,任意一个是对的,那么其他的都是错的。否则是全错。
来猜猜答案?
3 2 1 公布!
三个…都是错的!
这就是猜了,既然直到最少有两个错的,而且有可能全错,其实可以填全错,肯定有两个是对的。
来做一道题练练手吧!
12.1 练手题1
#include <cstdio>
using namespace std;
int n;
int a[100];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i)
scanf("%d", &a[i]);
int ans = 1;
for (int i = 1; i <= n; ++i) {
if (i > 1 && a[i] < a[i - 1])
ans = i;
while (ans < n && a[i] >= a[ans + 1])
++ans;
printf("%d\n", ans);
}
return 0;
}
咱们就做一道判断一道选择:
- 若将第 12 行的
<改为!=,程序输出的结果不会改变。()
A.对 B.错 - 最坏情况下,此程序的时间复杂度是()。
A. O(n^2)
B. O(log n)
C. O(n)
D. O(n log n)
答案
A
A
解析:
1.多跑几遍程序,没有什么影响。
2.严格单调递减,每次 if 都要重置 ans 。每次都要跑一边 while 。
故复杂度为 n^2 ,选 A。
12.2 练手题2
#include<iostream>
#include<cmath>
using namespace std;
double f(double a,double b,double c){
double s=(a+b+c)/2;
return sqrt(s*(s-a)*(s-b)*(s-c));
}
int main(){
cout.flags(ios::fixed);
cout.precision(4);
int a,b,c;
cin>>a>>b>>c;
cout<<f(a,b,c)<<endl;
return 0;
}
判断题
- (2分)当输入为
2 2 2时,输出为1.7321( ) - (2分)将第7行中的
(s-b)*(s-c)改为(s-c)*(s-b)不会影响程序运行的结果( ) - (2分)程序总是输出四位小数( )
单选题
- 当输入为
3 4 5时,输出为( )
A.6.0000
B.12.0000
C.24.0000
D.30.0000
5. 当输入为 5 12 13 时,输出为( )
A.24.0000
B.30.0000
C.60.0000
D.120.0000
答案
A
A
A
A
B
只要仔细观察,就可以观察出这是海伦公式,求三角形面积。
所以第四题三角形面积是6,第五题三角形面积是30,或者模拟程序都可以做对。
12.3 无敌的填空题目
前面两个都是CSP真题,现在我们来做一道老题,是填空题目:
//【NOIP 2009】普及组
#include <iostream>
using namespace std;
int main()
{
int a[3],b[3];
int i,j,tmp;
b[0]=2;
b[1]=3;
b[2]=5;
for (i=0;i<3;i++)
{
a[i]=0;
for (j=0;j<=i;j++)
{
a[i]+=b[j];
b[a[i]%3]+=a[j];
}
}
tmp=1;
for (i=0;i<3;i++)
{
a[i]%=10;
b[i]%=10;
tmp*=a[i]+b[i];
}
cout << tmp << endl;
return 0;
}
输出应该是?
答案
416
13. 完善程序
每个完善程序有5个空,每空三分。
完善程序方法:
1、读题:解决什么问题?题目给出了什么算法?输入如何转化输出?
2、明确变量的含义,通过变量单词的意思猜测;
3、大致想想:如果让你实现程序,你会怎么做。
4、通读程序,理顺程序结构,千万不要因为程序很长而觉得气馁,有时程序越长,填空越简单。
5、按照程序执行的顺序做,遇到难的先放一边。有些空格很简单,一下就能看出来的。
6、根据对程序的理解(结合自己已知的算法)大胆猜测,小心验证地填上很难的几个空。
7、填完了以后,再执行一遍程序,有样例就结合样例,没样例就自己造数据模拟。
来尝试一个:
答案
B
D
B
A
D
14. 总结
本帖已完结,总计约6000字。
最后,祝大家Bug–,RP++!