1.运算符号
字母,数字和+、-、*、/、=运算符均可以直接输入获得
命令$\cdot $ 表示乘法的圆点: \cdot
2.上下标
_表示下标,^表示上标,并且当上下标不止一个字符时,需用大括号括起来
单引号’表示求导
$ f(x_0)'=x^{2r}-x_0 $
f(x_0)'=x^{2r}-x_0
3.根式
开平方(2次根式)
用$ \sqrt{数}$来表示二次根式
$ \sqrt{2}$
\sqrt{2}
多次根式
用$ \sqrt[n]{x}$来表示x的n次方根
$ \sqrt[114514]{1919810}$
\sqrt[114514]{1919810}
4.分式、分数
用\frac{x1}{x2}来表示x2分之x1
$ \frac{Ju}{Ruo}$
\frac{Ju}{Ruo}
5.上下标记
命令:\overline, \underline 分别在表达式上、下方画出水平线
$\overline{xyz}$
$ \underline{abc}$
\overline{xyz}
\underline{abc}
命令:\overbrace, \underbrace 分别在表达式上、下方给出一个水平的大括号
$\overbrace{1+2+\cdots+n}^{n个}$
$ \underbrace{a+b+\cdots+z}_{26}$
\overbrace{1+2+\cdots+n}^{n个}
\underbrace{a+b+\cdots+z}_{26}
6. 向量
命令:\vec表示向量,\overrightarrow表示箭头向右的向量,\overleftarrow表示箭头向左的向量
$\vec{x} + \overrightarrow{AB} + \overleftarrow{DE}$
\vec{x} + \overrightarrow{AB} + \overleftarrow{DE}
7. 积分、极限、求和、乘积
命令:\int表示积分,\lim表示极限, \sum表示求和,\prod表示乘积 ,\infty表示无限
\mathrm{字符}表示把字母变成正体(自然对数底数e,虚数单位i和微分符号d需要使用正体)
$ \lim_{x \to \infty} x^2_{22} - \int_{1}^{5}x\mathrm{d}x + \sum_{n=1}^{20} n^{2} = \prod_{j=1}^{3} y_{j} + \lim_{x \to -2} \frac{x-2}{x} $
\lim_{x \to \infty} x^2_{22} - \int_{1}^{5}x\mathrm{d}x + \sum_{n=1}^{20} n^{2} = \prod_{j=1}^{3} y_{j} + \lim_{x \to -2} \frac{x-2}{x}
8. 三圆点
命令:\ldots点位于基线上,\cdots点设置为居中,\vdots使其垂直,\ddots对角线排列
$ x_{1},x_{2},\ldots,x_{5} \quad x_{1} + x_{2} + \cdots + x_{n} $
x_{1},x_{2},\ldots,x_{5} \quad x_{1} + x_{2} + \cdots + x_{n}
9. 重音符号
常用命令如下:
$ \hat{x} $
\hat{x}
$ \bar{x} $
\bar{x}
$ \tilde{x} $
\tilde{x}
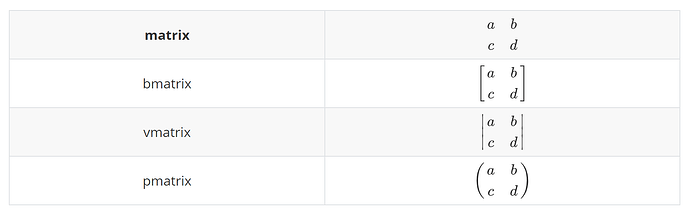
10.矩阵
详见下图:
下列代码中,&用于分隔列,\用于分隔行
$\begin{bmatrix}
1 & 2 & \cdots \\
67 & 95 & \cdots \\
\vdots & \vdots & \ddots \\
\end{bmatrix}$
\begin{bmatrix} 1 & 2 & \cdots \\ 67 & 95 & \cdots \\ \vdots & \vdots & \ddots \\ \end{bmatrix}
11. 希腊字母
希腊字母无法直接通过美式键盘输入获得。在LaTeX中通过反斜杠\加上其字母读音实现,将读音首字母大写即可输入其大写形式
$ \alpha^{2} + \beta = \Theta $
\alpha^{2} + \beta = \Theta
详见下表
12. 公式组合
通过cases环境实现公式的组合,&分隔公式和条件,还可以通过\limits来让x→0位于lim的正下方而非默认在lim符号的右下方显示
$D(x) = \begin{cases}
\lim\limits_{x \to 0} \frac{a^x}{b+c}, & x<3 \\
\pi, & x=3 \\
\int_a^{3b}x_{ij}+e^2 \mathrm{d}x,& x>3 \\
\end{cases}$
D(x) = \begin{cases} \lim\limits_{x \to 0} \frac{a^x}{b+c}, & x<3 \\ \pi, & x=3 \\ \int_a^{3b}x_{ij}+e^2 \mathrm{d}x,& x>3 \\ \end{cases}