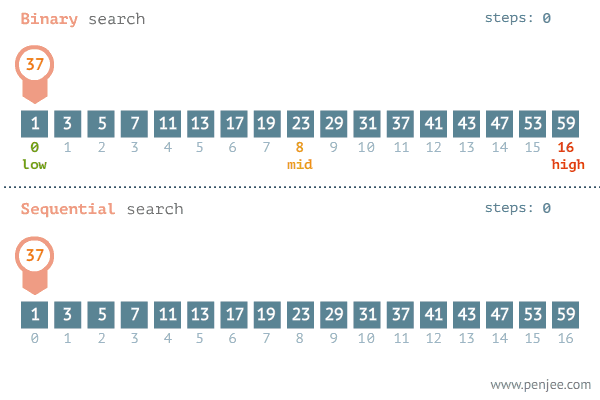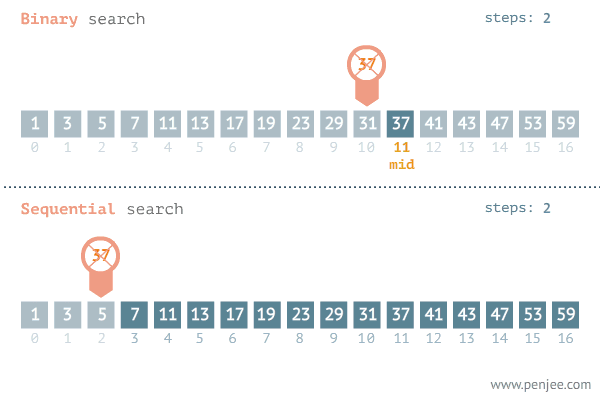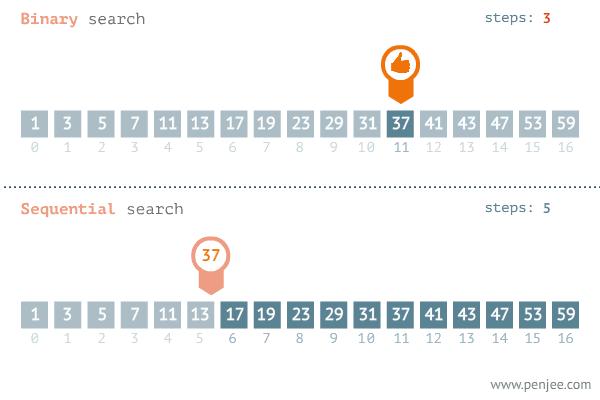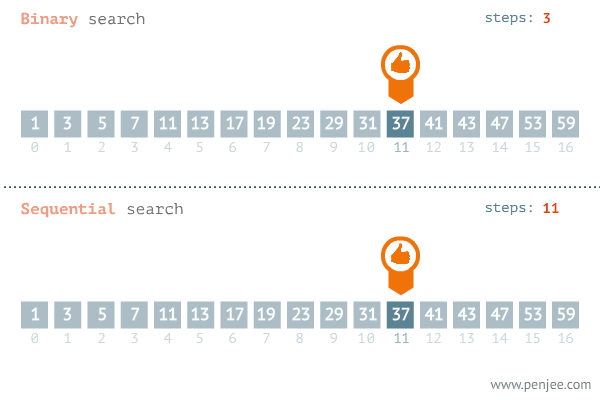
二分查找(
中分查找),顾名思义,是一种查找算法,每次取数据中的中间值,时间复杂度通常为O(log2(n).
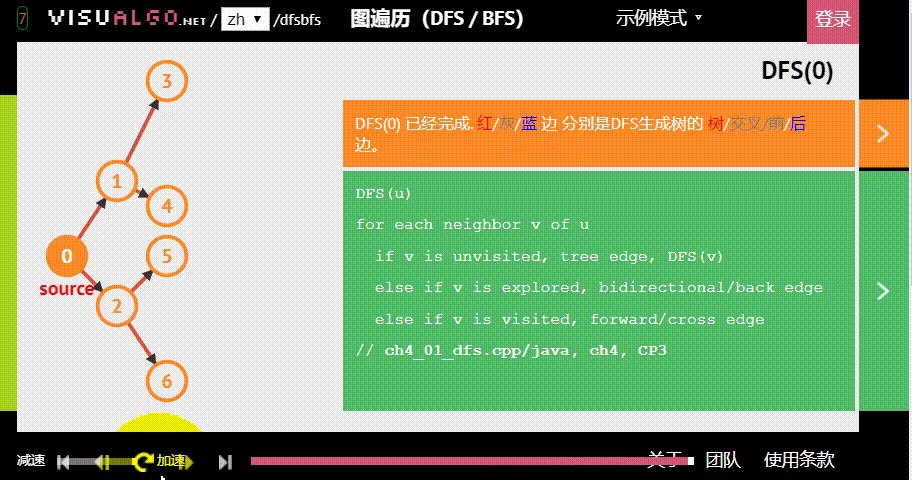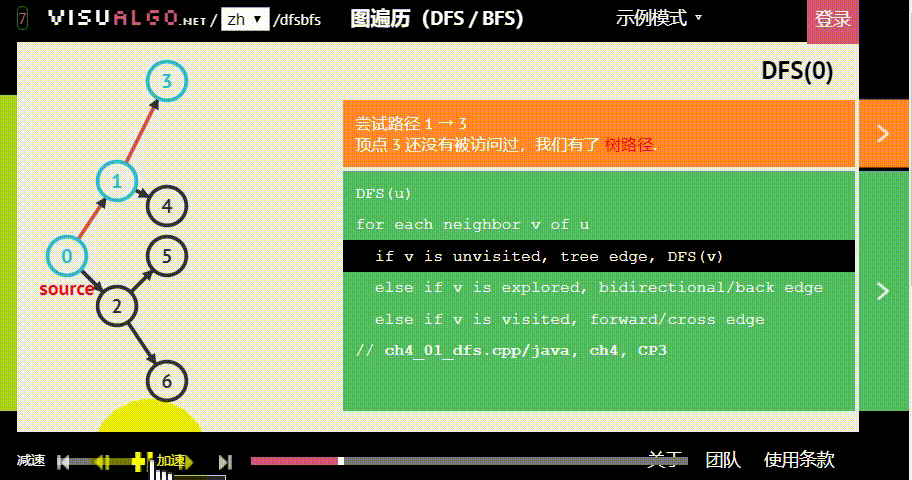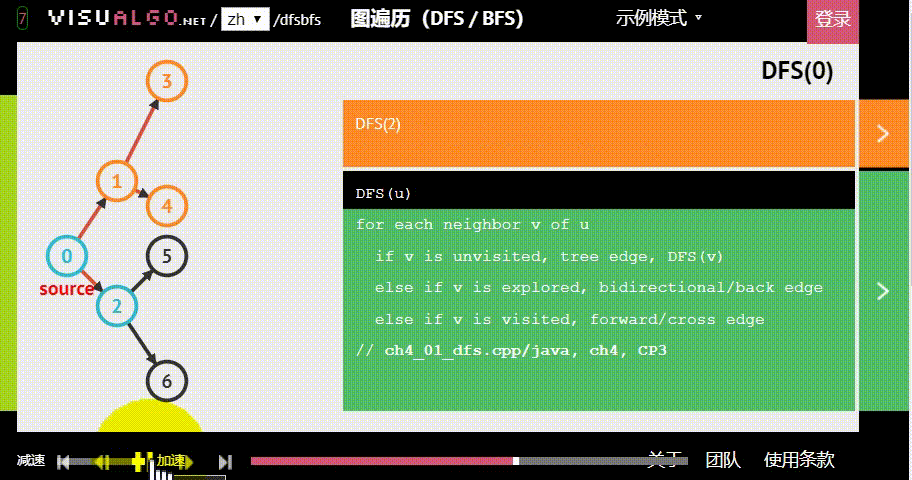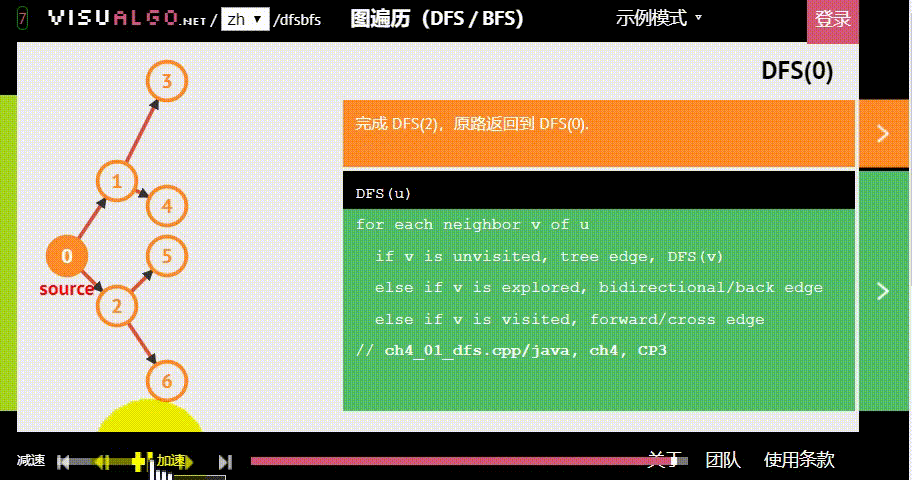
深度优先搜索(DFS)顾名思义是一种搜索算法,每次“不撞南墙不回头”。一般用栈或递归来实现,时间复杂度通常为O(2^n)或O(n^2)
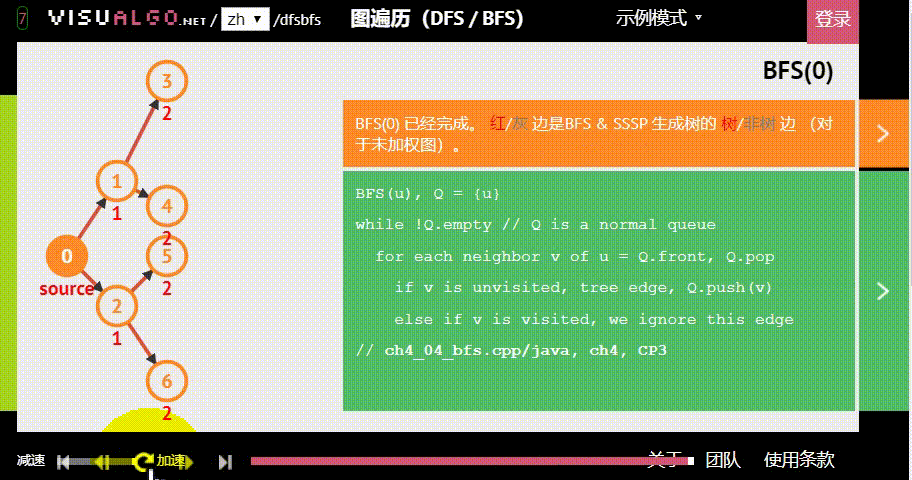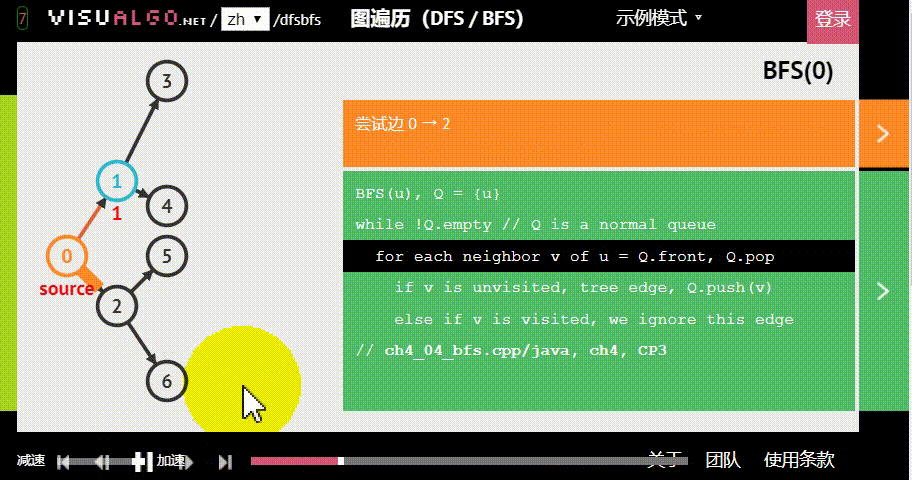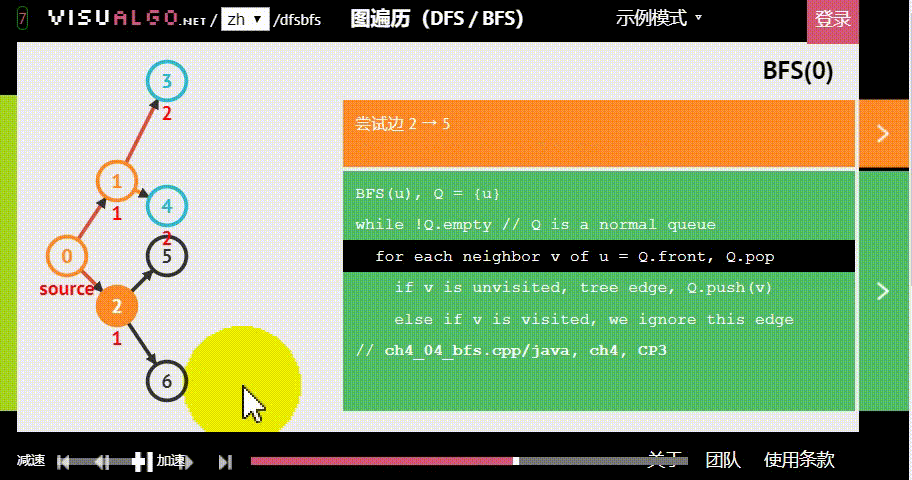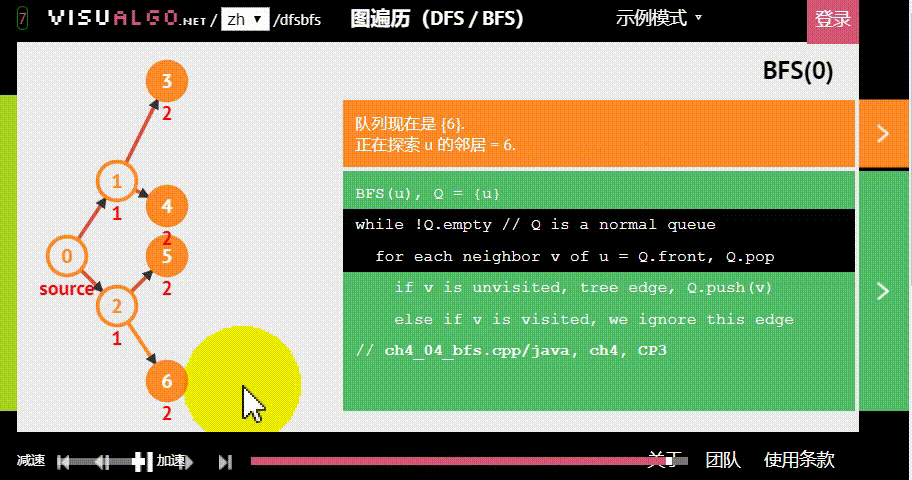
广度优先搜索(BFS),也被称为宽度优先搜索,也是一种搜索算法,每次有“分身”来进行查找,就像网络的传播,所以时间复杂度会比 深度优先搜索(DFS)略快一点
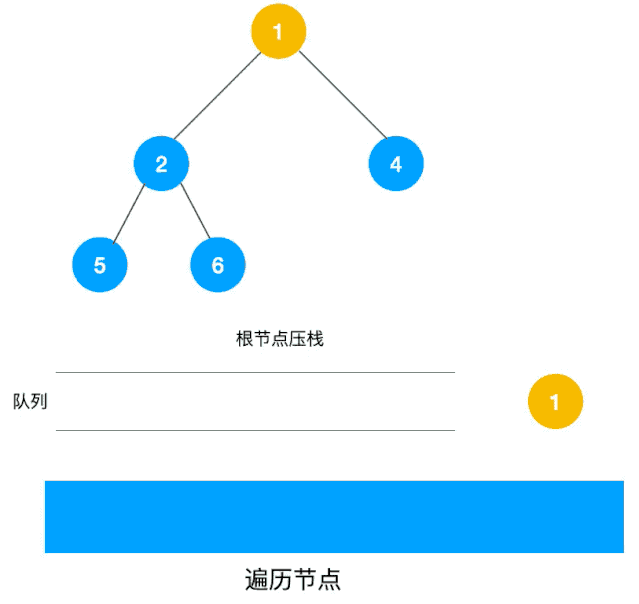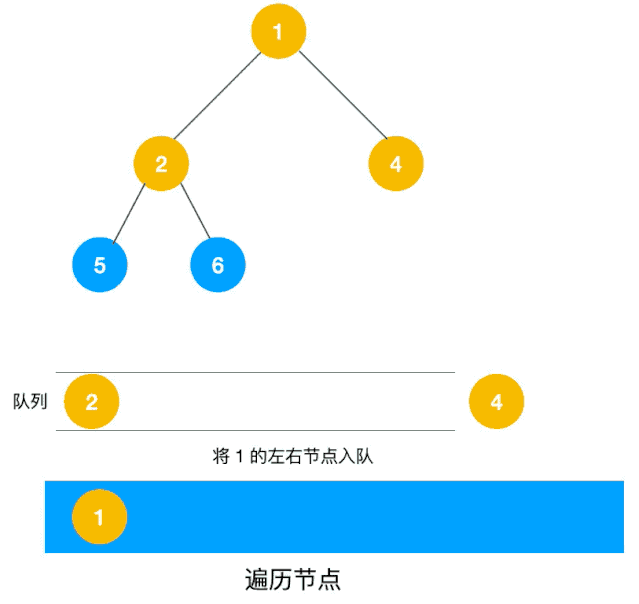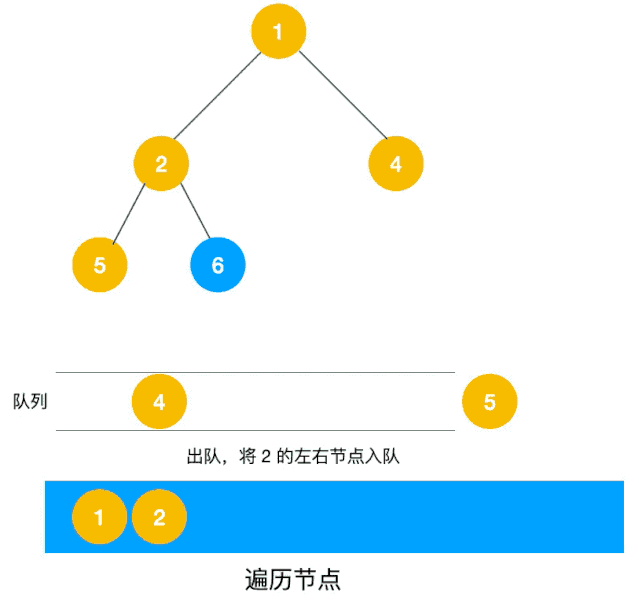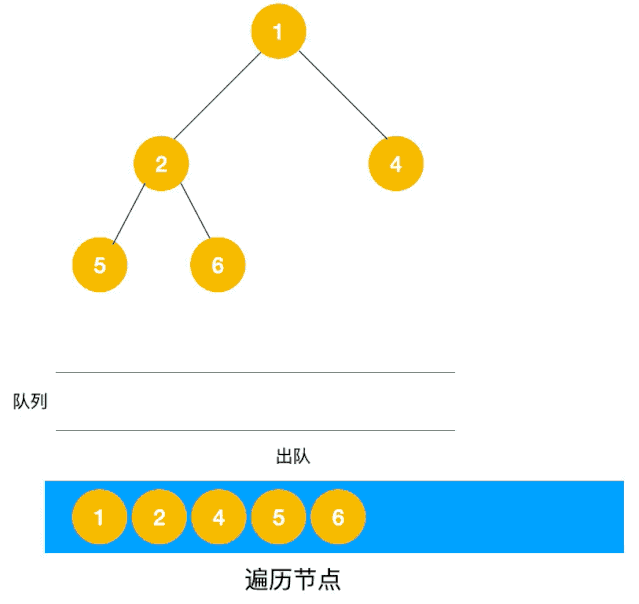
记忆化搜索是一种通过记录已经遍历过的状态的信息,从而避免对同一状态重复遍历的搜索实现方式。
那它们有什么不同呢?
当问题的答案具有某种单调性时,我们就可以二分答案。 单调性可以理解为,随着x的增加,对应y值逐渐增大——单调递增;或者随着x的减小,对应y值逐渐减小——单调递减。
深度优先搜索(DFS)与 广度优先搜索(BFS)其实都是一种暴力程序,时间复杂度都较高。
记忆化搜索确保了每个状态只访问一次,它也是一种常见的动态规划(dp)实现方式。你可以理解为:
记忆化搜索=搜索的形式+动态规划(dp)的思想
二分查找模板:
int l=1,r=n+1,mid;
while(l<r)
{
mid=(l+r)>>1;//或者 mid=l+(r-l)>>1;
if(a[mid]>=x) r=mid;
else l=mid+1;
}
cout<<l;
深度优先搜索(DFS)模板:
void DFS(type n){//当前搜索的是第几个节点
if(符合条件) cout<<答案;return;//递归的出口
for(//选择该阶段的可以访问的所有节点){
标记已访问该点;
DFS(n+1); //进入下一阶段,往下递归
还原访问现场;
}
}
广度优先搜索(BFS)模板:
void bfs(起始状态){
queue<int> qu;//创建队列
qu.push(起始状态入队);
//起始状态标记
while(!qu.empty()){//当队列非空
//获取从起始状态可以到达的下一个点
if(这个点可以走)
qu.push(当前状态);//该状态入队
…………………
处理(队首)qu.top();
相应操作;
qu.pop();//队首弹出队
}//一次循环结束,执行下一次循环
}
记忆化搜索模板:
int dfs()
{
if(有解) return 解;
for(枚举路径总数)
if(满足条件)
{
if(到达目的)return 值;
else
{
int t=dfs(继续递归);
找出最优值;
}
}
储存最优值;
return 最优值;
}
综上所述,如果问题是一个单调性的序列的话,那么使用优先级是:
二分查找 > 记忆化搜索 > 广度优先搜索(BFS)> 深度优先搜索(DFS)
但如果问题无单调性,那么二分查找将无法使用
记忆化搜索也不适用于求连通块等题目
所以同学们要根据题目选择适当的搜索算法!
你们喜欢哪种搜索算法?
- 二分查找
- 深度优先搜索(DFS)
- 广度优先搜索(BFS)
- 记忆化搜索
0
投票人