强连通等
定义
- 连通分量:连通的子图
- 极大连通分量:最大的连通分量(不能再加点)
- 强连通分量:任意两个点之间都互相可达
- 极大强连通分量:最大的强连通分量(不能再加点)
Tarjan
-
求强连通分量
-
把强连通分量缩成一个点后变成一张 DAG
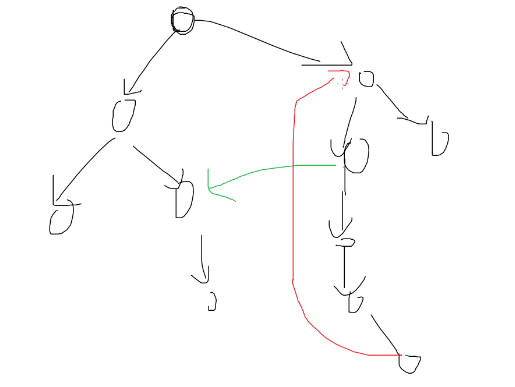
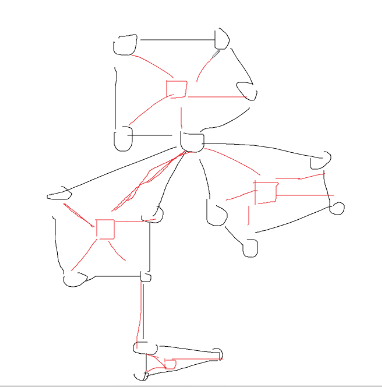
- 原理图
-
树边:dfs 树上的边(图中黑色的边)
-
返祖边:回到自己祖先的一条边(图中红色的边)
-
横插边:除上面两种边外的边(图中绿色的边)
-
因为横插边不可能形成强连通分量所以直接无视
-
dfn表示点的 dfs 序编号,low表示通过返祖边仅向上爬一次能到达的最浅深度 -
在求强连通分量时爬多少次无所谓,但求割点的时候会出问题
-
如果
dfn[u] == low[u]就说明u是一个强连通分量的根(即既没有一条起点是u的返祖边,也没有返祖边跨过它) -
此时将栈里的点弹到直到弹到这个点(强连通分量的根),它们就属于一个强连通分量
-
强连通分量性质:
割点和割边
-
求割点:
-
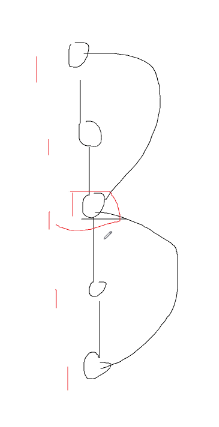
还是用 Tarjan ,但是每次求
low时只能向上爬一次 -
如图:
-
如果可以向上爬多次,那每个点的
low就都是 1 了,区别不出来割点是什么 -
如果一个点被一条返祖边跨越,则这个既不是强连通分量中深度最浅的点,也不是割点
-
但如果这个点上长者一条返祖边,则该点也可能是割点
-
所以只能沿着返祖边跳一次
-
所以割点有两种:要么是根,要么没有返祖边跨越他且他有孩子(不能是叶子节点)
- 求割边(桥):
![]()
双连通
- 点双:没有割点的图
- 边双:没有割边的图
- Tarjon,割点,割边,点双,边双实现详解
2-SAT 问题
- n-SAT 当 n\ge3 时这是个 NPC 问题(即复杂度不能是多项式级别的问题)
- 但 2-SAT 可以用强连通分量求解
- 这种情况就是无解,否则可以证明一定有解
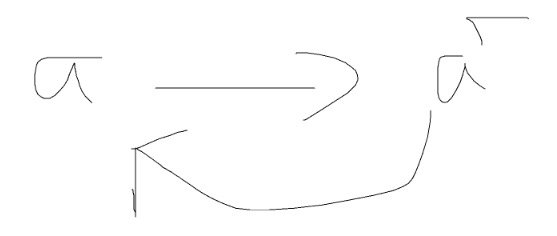
- 对建出的图求强连通分量后缩点,得出一张 DAG
- 然后求拓扑序,对于每个变量 a,\neg a ,把拓扑序小的赋值为 0 ,大的赋值为 1
- 2-SAT详解
例题
P4171 [JSOI2010] 满汉全席
- 裸的 2-SAT 板子
P3825 [NOI2017] 游戏
- 乍一看是 3-SAT 耶!
- 其实如果当前地图不适合 x 赛车,就对剩下的 y 和 z 去建边(要么选 y ,要么选 $z$)
- 如果是通用赛车图? 3^8 枚举?
- 2^8 就够了,因为选 a 车和 b 车已经包含了选 c 车的情况
P4630 [APIO2018] 铁人两项
- 如果是一棵树,暴力枚举切断点,按顺序合并
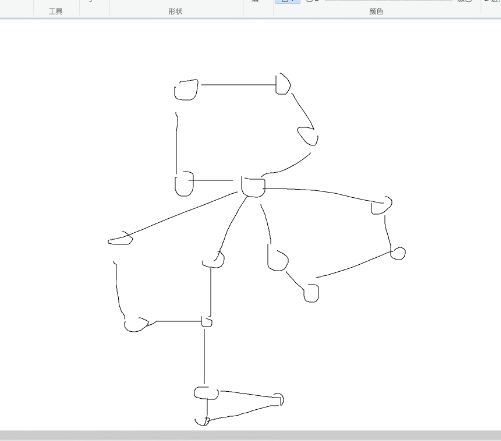
- 要用到仙人掌结构:
-
图中有 4 个环
-
对于每个环建一个方点,留下红色的边和树边
-
这样子剩下的图一定是棵树(圆方树)
先把所有的点双求出来
对于每个点双都能在里面取起点、中转点和终点
然后排列组合求出答案
方点连接割点的边边权为 0
后面相当于把最短路拆成边建
每个点到方点的边权为割点到该点的最短路
—— wsr
课后题
守矢的关键路径
-
法一:正着求一遍拓扑算出最早开始时间,反着求一遍拓扑算出最晚开始时间,如果最早开始时间与最晚开始时间相等,则该点一定在关键路径上
#include <bits/stdc++.h> using namespace std; const int maxn = 15000 + 10; struct cc { int from, to, cost; } es[maxn]; struct cc2 { int from, to, cost; } es2[maxn]; int ru[maxn], ru2[maxn], first[maxn], nxt[maxn], dis[maxn], first2[maxn], nxt2[maxn], dis2[maxn]; bool vis[maxn], vis2[maxn]; int tot = 0; void build(int ff, int tt, int pp) { es[++tot] = (cc) { ff, tt, pp }; nxt[tot] = first[ff]; first[ff] = tot; } int tot2 = 0; void build2(int ff, int tt, int pp) { es2[++tot2] = (cc2) { ff, tt, pp }; nxt2[tot2] = first2[ff]; first2[ff] = tot2; } int n, m; void TopoSort() { // 求各点最早发生时间 for (int i = 1; i <= n; i++) { if (!ru[i] && !vis[i]) { vis[i] = 1; for (int j = first[i]; j; j = nxt[j]) { int u = es[j].to; dis[u] = max(dis[u], dis[i] + es[j].cost); if (!vis[u]) { ru[u]--; if (!ru[u]) { TopoSort(); } } } } } } void TopoSort2() { // 求各点最晚发生时间 for (int i = n; i >= 1; i--) { if (!ru2[i] && !vis2[i]) { vis2[i] = 1; for (int j = first2[i]; j; j = nxt2[j]) { int u = es2[j].to; dis2[u] = min(dis2[u], dis2[i] - es2[j].cost); if (!vis2[u]) { ru2[u]--; if (!ru2[u]) { TopoSort2(); } } } } } } int main() { memset(dis2, 63, sizeof(dis2)); scanf("%d%d", &n, &m); for (int i = 1; i <= m; i++) { int x, y, z; scanf("%d%d%d", &x, &y, &z); build(x, y, z); build2(y, x, z); ru[y]++, ru2[x]++; } TopoSort(); dis2[n] = dis[n]; TopoSort2(); int ans = 0; for (int i = 1; i <= n; i++) if (dis[i] == dis2[i]) ans++; printf("%d", ans); return 0; } -
法二:用 Dijkstra 建出最长路径树,记录每个点的转移前驱,最后 dfs 搜一遍最长路径上的点(我自己想的做法 qwq)
#include<bits/stdc++.h> #define mk make_pair #define type pair<int,int> using namespace std; const int maxn = 205; int n,m,dis[maxn],ans; bool vis[maxn]; vector<pair<int,int> > mp[maxn]; vector<int> dfn[maxn]; void addEdge(int u,int v,int w) { mp[u].push_back(mk(v,w)); } void Dijkstra() { priority_queue<type,vector<type>,greater<type> > q; memset(dis,-0x3f,sizeof(dis)); dis[1] = 0; q.push(mk(0,1)); while (!q.empty()) { type top = q.top(); q.pop(); int u = top.second; vis[u] = true; for (auto v : mp[u]) if (dis[v.first] < dis[u] + v.second) { dfn[v.first].clear(); dfn[v.first].push_back(u); dis[v.first] = dis[u] + v.second; if (!vis[v.first]) q.push(mk(dis[v.first],v.first)); } else if (dis[v.first] == dis[u] + v.second) dfn[v.first].push_back(u); } // for(int i = 1;i <= n;i ++) cout << dis[i] << ' '; } void dfs(int u) { if (vis[u]) return ; ans ++, vis[u] = true; for (auto v : dfn[u]) dfs(v); } int main() { scanf("%d%d",&n,&m); for (int i = 1,u,v,w;i <= m;i ++) { scanf("%d%d%d",&u,&v,&w); addEdge(u,v,w); } Dijkstra(); memset(vis,false,sizeof(vis)); dfs(n); printf("%d",ans); return 0; }
最大半连通子图
-
思路在代码里 qwq
/* 首先观察到这个图中如果有某个部分是强连通的,那就不会对半连通子图产生贡献 所以首先对这个图进行t缩点 并记录下每个连通块的大小和每个点所在的连通块 然后对图求出最长链个数和长度 按照拓扑序进行 dp: f[i] 表示到第 i 个连通块的最长链大小, g[i] 表示个数。 很容易就想到了转移的方法: 1.{g[i]=g[i]+g[j]}(条件:f[j]+number[i]==f[i]) 2.{g[i]=g[j],f[i]=f[j]+number[i]}(条件:f[j]+number[i]>f[i])。 按照这个转移状态就可以啦。 但是要注意缩点之后会出现大量重边拓扑排序之前要去重。 */ #include<bits/stdc++.h> #define mk make_pair using namespace std; const int maxn = 1000005; int n,m,P,dfn[maxn],low[maxn],tot,top,cnt,f[maxn],g[maxn],len[maxn],d[maxn],siz[maxn],st[maxn],b[maxn]; bool vis[maxn]; vector<int> mp[maxn],nmp[maxn]; vector<pair<int,int> > edge; void addEdge(int u,int v) { mp[u].push_back(v); } void addnewEdge(int u,int v) { nmp[u].push_back(v); d[v] ++; } void Tarjan(int u) { dfn[u] = low[u] = ++ tot, vis[u] = true, st[++ top] = u; for (auto v : mp[u]) if (!dfn[v]) { Tarjan(v); low[u] = min(low[u],low[v]); } else if (vis[v]) low[u] = min(low[u],dfn[v]); if (low[u] == dfn[u]) { siz[++ cnt] = 1, b[u] = cnt; while (st[top] != u) b[st[top]] = cnt, siz[cnt] ++, vis[st[top]] = false, top --; top --, vis[u] = false; } } void build() { for (int u = 1;u <= n;u ++) for (auto v : mp[u]) if (b[u] != b[v]) edge.push_back(mk(b[u],b[v])); sort(edge.begin(),edge.end()); int i = 0; for (auto E : edge) { int u = E.first, v = E.second; if (i > 0 && edge[i - 1].first == u && edge[i - 1].second == v) { i ++; continue; } addnewEdge(u,v); i ++; } } void Solve() { queue<int> q; for (int i = 1;i <= cnt;i ++) { if (d[i] == 0) q.push(i); f[i] = siz[i], g[i] = 1; } while (!q.empty()) { int u = q.front(); q.pop(); for (auto v : nmp[u]) { d[v] --; if (f[u] + siz[v] == f[v]) g[v] = (g[u] + g[v]) % P; else if (f[u] + siz[v] > f[v]) f[v] = f[u] + siz[v], g[v] = g[u]; if (!d[v]) q.push(v); } } } int main() { scanf("%d%d%d",&n,&m,&P); for (int i = 1,u,v;i <= m;i ++) { scanf("%d%d",&u,&v); addEdge(u,v); } memset(low,0x3f,sizeof(low)); for (int i = 1;i <= n;i ++) if (!dfn[i]) Tarjan(i); build(); Solve(); int pos = 0,k = 0; for (int i = 1;i <= cnt;i ++) if (f[i] > f[pos]) pos = i, k = g[pos]; else if (f[i] == f[pos]) k = (k + g[i]) % P; printf("%d\n%d",f[pos],k); return 0; }
Grass Cownoisseur
-
先把强连通分量缩起来,记录每个连通块的大小
-
正反跑两遍最长路,最后枚举每个连通块并更新答案
#include<bits/stdc++.h> #define mk make_pair using namespace std; const int maxn = 1e5 + 5; int n,m,dis1[maxn],dis2[maxn]; vector<int> mp[maxn],nmp1[maxn],nmp2[maxn]; bool vis[maxn]; int dfn[maxn],low[maxn],tot,cnt,st[maxn],top,b[maxn],siz[maxn]; vector<pair<int,int> > e; void addEdge(int u,int v) { mp[u].push_back(v); } void Tarjan(int u) { dfn[u] = low[u] = ++ tot, st[++ top] = u, vis[u] = true; for (auto v : mp[u]) if (!dfn[v]) { Tarjan(v); low[u] = min(low[u],low[v]); } else if (vis[v]) low[u] = min(low[u],dfn[v]); if (dfn[u] == low[u]) { siz[++ cnt] = 1, b[u] = cnt; while (st[top] != u) b[st[top]] = cnt, siz[cnt] ++, vis[st[top]] = false, top --; vis[u] = false, top --; } } void addnewEdge(int u,int v) { nmp1[u].push_back(v); nmp2[v].push_back(u); } void build() { for (int i = 1;i <= n;i ++) for (auto j : mp[i]) if (b[i] != b[j]) e.push_back(mk(b[i],b[j])); sort(e.begin(),e.end()); int i = 0; for (auto E : e) { int u = E.first, v = E.second; if (i > 0 && e[i].first == u && e[i].second == v) { i ++; continue; } addnewEdge(u,v); } } void SPFA1() { queue<int> q; q.push(b[1]); memset(vis,false,sizeof(vis)); memset(dis1,-0x3f,sizeof(dis1)); dis1[b[1]] = siz[b[1]]; while (!q.empty()) { int u = q.front(); q.pop(); vis[u] = false; for (auto v : nmp1[u]) { if (dis1[v] < dis1[u] + siz[v]) { dis1[v] = dis1[u] + siz[v]; if (!vis[v]) { vis[v] = true; q.push(v); } } } } } void SPFA2() { queue<int> q; q.push(b[1]); memset(vis,false,sizeof(vis)); memset(dis2,-0x3f,sizeof(dis2)); dis2[b[1]] = siz[b[1]]; while (!q.empty()) { int u = q.front(); q.pop(); vis[u] = false; for (auto v : nmp2[u]) { if (dis2[v] < dis2[u] + siz[v]) { dis2[v] = dis2[u] + siz[v]; if (!vis[v]) { vis[v] = true; q.push(v); } } } } } int main() { scanf("%d%d",&n,&m); for (int i = 1,u,v;i <= m;i ++) { scanf("%d%d",&u,&v); addEdge(u,v); } for (int i = 1;i <= n;i ++) if (!dfn[i]) Tarjan(i); build(); SPFA1(); SPFA2(); int ans = siz[b[1]]; memset(vis,false,sizeof(vis)); for (int i = 1;i <= n;i ++) if (!vis[b[i]] && dis1[b[i]]) { int u = b[i]; vis[u] = true; for (auto v : nmp2[u]) { if (!dis2[v]) continue; ans = max(ans,dis1[u] + dis2[v] - siz[b[1]]); } } printf("%d",ans); return 0; }