线性dp复习笔记
最长上升子序列
dp[i] 表示以第 i 个元素为结尾的最长上升子序列的长度
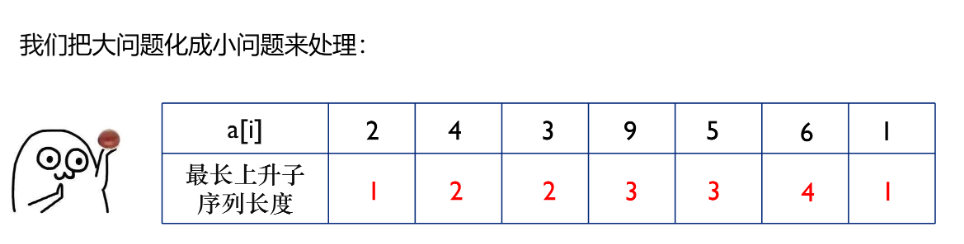
如果 a[i]>a[j] 时 dp[i]=max(dp[i],dp[j]+1)
因为每个数本身都是一个上升子序列 所以初始时 dp[i]=1
模板
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
if(a[i]>a[j]) dp[i]=max(dp[i],dp[j]+1);
}
ans=max(ans,dp[i]);
}
最长公共子序列
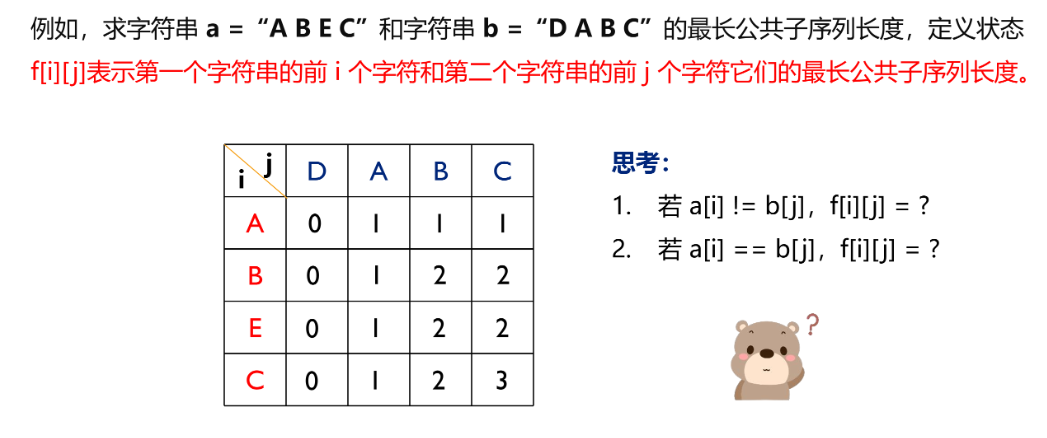
模板
for(int i=1;i<=len_a;i++){
for(int j=1;j<=len_b;j++){
if(a[i]==b[j]) dp[i][j]=dp[i-1][j-1]+1;
else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
最大子段和
dp[i] 表示以第 i 个元素为结尾的最大子段和
模板
for(int i=1;i<=n;i++){
dp[i]=max(dp[i-1]+a[i],a[i]);
ans=max(ans,dp[i]);
}
经典例题

我们可以将所有信封按 w[i] 进行升序排序 h[i] 进行降序排序
bool cmp(let x,let y){
if(x.w!=y.w) return x.w<y.w;
else return x.h>y.h;
}
因为当 i<j 时 w[i]\le w[j] 且当 w[i]=w[j] 时 h[i]\ge h[j]
所以整个问题就转换为了求 h 的最长上升子序列
for(int i=1;i<=n;i++){
for(int j=i;j>=1;j--){
if(le[i].h>le[j].h) dp[i]=max(dp[i],dp[j]+1);
}
ans=max(dp[i],ans);
}
时间复杂度为 O(N^2) 因为 n \le10^5 所以超时是必然的
根据数据范围猜算法 时间复杂度应为 O(NlogN) 考虑二分
我们可以建一个动态数组 dp
dp[i] 表示长度为 i+1 的递增子序列的最小末尾高度
遍历结束后 dp.szie() 即为所求
对于每个 h[i] 我们在 dp 中二分查找第一个 \ge h[i] 的位置 l
如果 l=dp.size()
说明 h[i] 比 dp 中的任何一个数都要大
结合上述排列规则
我们可以得到 h[i] 所对应的 w[i] 也比 dp 中的任何一个 h[i] 所对应的 w[i] 要大
所以我们此时可以将此时的 h[i] 加入到 dp 中
否则则意味我们能在 dp 中找到一个$\ge h[i]$ 的数
此时我可以将 dp[l] 的值替换为 h[i]
为什么可以替换?为什么要替换?
因为我只进行了替换 并未使数组大小发生改变
所以替换操作在维护原先答案的前提下最优子序列的末尾高度
为后续操作提供更多的嵌套可能
如
原 dp 中的 (w,h) 分别为 (3,1)(4,6)(6,7)
此时添加一对 (7,5) 数组发生改变 (3,1)(7,5)(6,7)
下次如果可以添加 只需与数组中当前长度下最优的末尾高度比较
否则就再次优化末尾高度
这也就解释了上面两个问题并保证了数据单调性及二分可行性
代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
struct let{
int w,h;
}le[N];
bool cmp(let x,let y){
if(x.w!=y.w) return x.w<y.w;
else return x.h>y.h;
}
int n,ans;
vector<int> dp;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>le[i].w>>le[i].h;
}
sort(le+1,le+1+n,cmp);
for(int i=1;i<=n;i++){
int l=0,r=dp.size();
while(l<r){
int mid=(l+r)/2;
if(le[i].h<=dp[mid]) r=mid;
else l=mid+1;
}
if(l==dp.size()) dp.push_back(le[i].h);
else dp[l]=le[i].h;
}
cout<<dp.size();
}