1.矩阵入门
线性代数
线性代数是在 OI 中应用十分广泛的领域之一,在很多常见问题中都有使用,例如:
1.解 n 元 1 次方程。
2.求无向图的生成树数量。
3.询问 n 个数所有子集不同异或和的数量。
……
矩阵是线性代数中最为重要的概念与数学工具,故从矩阵切入。
什么是矩阵?
矩阵的定义:由 n\times m 个数组成的 n 行 m 列的数表(可以将一个 n 行 m 列的矩阵看作一个 n\times m 的二维数组):
叫做 n 行 m 列的矩阵,简称 n\times m 的矩阵。
特殊地, n=m 时,称为 n 阶方阵。
其中 1\times n (或 n\times 1 )的矩阵较为特殊,被称为向量。(可以将一个向量视作一个长度为n的一维数组)
其中 1\times n 的向量被称为行向量, n\times 1 的向量被称为列向量。
矩阵的加减法
矩阵的加减法非常简单:
例如:
注:两矩阵都必须是 n\times m 的矩阵。
矩阵乘法
矩阵与常数的乘法
简单地将矩阵内的所有元素乘上该数即可。例如:
矩阵与矩阵的乘法(重要)
假设 A 是一个 n\times m 的矩阵, B 是一个 m\times k 的矩阵,则它们可以相乘并得到一个 n\times k 的矩阵 C 。
计算的规则为:
称 A\times B = C。
附一张图更好理解:
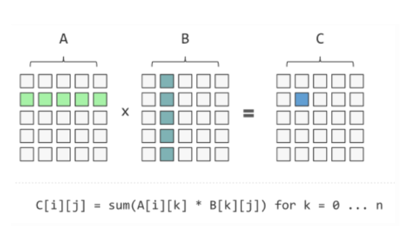
注意:
- 对于两个矩阵 A 和 B , 只有当 A 的列数与 B 的行数相同时, A \times B 才有意义。显然,矩阵乘法不存在交换律,因为可能 A \times B 存在而 B\times A 不存在。
- 矩阵乘法具有结合律与分配律,即:
- A\times (B\times C) = (A\times B)\times C
- A\times(B+C) = A\times B+A\times C
矩阵乘法代码:

时间复杂度: O(n^3)
2.矩阵快速幂
众所周知,快速幂算法可以在计算 a 的 b 次方的时候让运算时间来到 O(\log b) 级别,但是为什么能这么做吗?
其实是因为常数的乘法运算符合结合律, a^6 = a\times a\times a\times a\times a\times a 由于可以使用结合律,因此也可以写作 (a\times a)\times(a\times a\times a\times a) = a^2\times a^4
总结
往往能够使用结合律的算法,都能使用快速幂(倍增)算法进行加速。
欸,矩阵乘法也有结合律,那是不是也能用快速幂增速呢? ![]()
![]()
当然可以,类比普通快速幂,我们可以得到这样的算法:
计算 A 的 2 的次幂,即 A^1,A^2,A^4,A^8,\dots,A^{2^{\lfloor\log_2 k\rfloor}}
考虑 k 的二进制,设 k_i 为从低到高第 i 为的值 (从 0 开始)那么:
代码:
matrix ksm(matrix x,int k){
matrix res,now = x;
memset(res.a,0,sizeof res.a);
for(int i = 1;i<=n;i++)res.a[i][i]=1;
while(k){
if(k&1)res = res*now;
now = now*now,k>>=1;
}
return res;
}
例题
- 洛谷P3390 【模板】矩阵快速幂
传送门
纯板子,直接套用上面的模板即可。 - P1962 斐波那契数列
传送门
注意到 1\le n\le 2^{63} ,正常线性递推肯定过不了,于是就有了矩阵快速幂优化线性递推这个知识点了。
已知 f_n = f_n-1 + f_n-2 (斐波那契数列递推式) 我们可以用矩阵来描述这种关系。
为啥是乘这个矩阵呢?
首先确定目标矩阵。下面是我想要的矩阵:
根据递推式就可以得到下面两个式子:
就可以得到矩阵了。
接着,又已知 f_0 = 0,f_1 = 1 那么:
那么,只需计算出中间的矩阵的 n-1 次幂,就能求出 f_n 了。时间复杂度 O(\log n) 。
拓展:P1349 P1939 P1306