作用
AC自动机(Aho-Corasick自动化机)是一种高效的多模式匹配算法,主要用于在文本中同时查找多个关键词,具有处理大规模数据和实时搜索的能力。
实现方法
本质上需要字典树(trie), AC自动机是以字典树为结构基础,KMP算法建立的自动机。
构建Tire:
假设现在有几个单词:
\left \{ abca,bcb,ca,cc,d \right \}
那么我们可以以节点0( root )为起始构造一棵Tire:
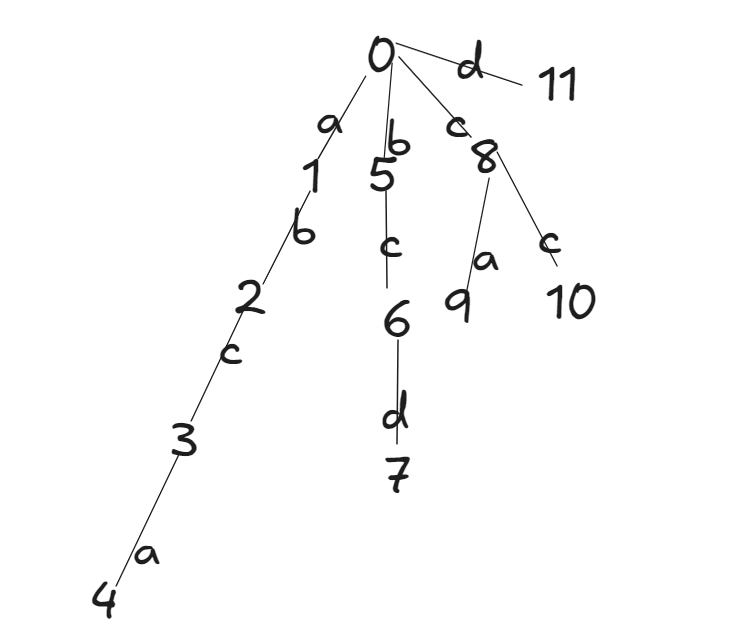
AC 自动机在初始时会将若干个模式串插入到一个 Trie 里,然后在 Trie 上建立 AC 自动机。这个 Trie 就是普通的 Trie,按照 Trie 原本的建树方法建树即可。
依照这棵字典树:我们可以列出一下的表,意思是从节点 i 可以通向节点 j
abca 就是 图中的 4, bcd 就是图中的 7 , ca 就是图中的 9, cc 就是图中的 10, d 就是图中的 11
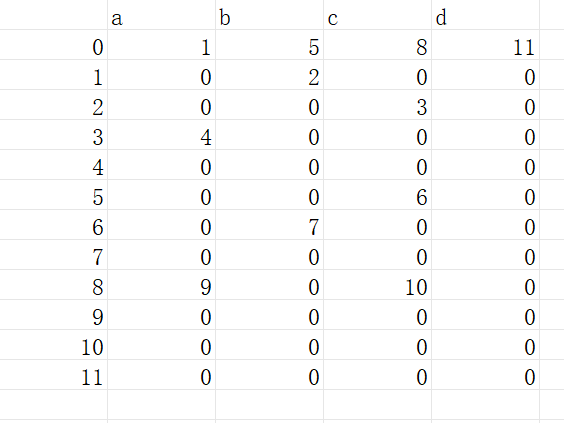
其中0表示不通向任何节点。
我们可以给我们的单词给出编号:
fail指针(失配指针)
根据我们的表,我们可以给出失配指针(注意失配指针的建立实际上是bfs 的过程)
注意 fail 指针的作用是在当前的位置的下一个匹配失败了,回到最大匹配的位置,那实现过程就是看上一项的最大配位,寻找最长的相同前后缀。
实现过程:
对于我们现在建出的 Tire, 我们给出全模拟过程:
假设我们现在在 1,5,8,11 的节点匹配失败了, 我们的 fail 指针指向 0 节点。
当我们在 2 节点匹配失败了,我们可以取找他的父节点 1 节点, 1 节点的 fali 指针指向 0 节点, 而节点 0 有子节点 5 是 b 所以 2 的 fail 指针指向 5
……
对于所有的节点,当匹配失败的时候,我们就找他的父节点,然后使用已经建成的 fail 指针,直到找到某个节点有子节点和这个节点的后缀相同为止。
我们现在可以列出 fail 指针的列表:
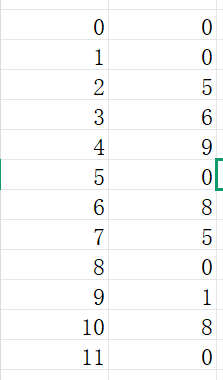
现在为了实现功能我们这样:
假设现在有一段文本 dabcabcbcca
首先我们走向 11 因为 11 对应 d 我们将 11 的 值 + 1,以及他的 fali 指针指向的节点 0 (因为 0 节点本身不存在,所以不需要将 fail 指针指向的数字 + 1本来需要将fail指针 + 1)
下一个字母 a, 11 没有节点直接指向 a, 我们取找他的 fail 指针指向的数字 0 它有子节点 1 对应的字母是 a 所以我们从 11 走向 1
……
总结以上步骤:
- 如果本节点有子节点和当前的字母相匹配,那么直接走到子节点就可以了, 并且将将子节点,以及它的 fail 指针指向的节点 +1, 如果指向的节点还有 fail 指针,那么我们继续将他的 fail 指针指向的节点 +1, 直到 节点 0 为止
- 如果本节点没有子节点和当前的字母相匹配,那么我们就走他的 fail 指针指向的节点,再寻找此节点的子节点有没有与本字母相匹配的字母,否则继续找他的 fail 指针, 直到寻找到为止,同时将寻找到的节点 +1, 并且将它的 fail 指针指向的节点 +1, 如果指向的节点还有 fail 指针,那么我们继续将它的 fail 指针指向的节点 +1,直到 节点 0 为止
这样我们惊奇的发现,编号 4, 7, 9, 10, 11 对应的数字就是我们的单词表中的单词出现的次数。
优化
因为我们的 AC 自动机中,每次匹配,会一直向 fail 边跳来找到所有的匹配,但是这样的效率较低,在某些题目中会超时。那么需要如何优化呢?首先需要了解到 fail 指针的一个性质:一个 AC 自动机中,如果只保留 fail 边,那么剩余的图一定是一棵树。这是显然的,因为 fail 不会成环,且深度一定比现在低,所以得证。这样 AC 自动机的匹配就可以转化为在 fail 树上的链求和问题,只需要优化一下该部分就可以了。(类似建反图)
这里推荐使用 dfs 优化,(还有一种是拓扑排序)(个人感觉 dfs 代码好写一点)
void dfs(int u)
{
for (int i = head[u]; i != 0; i = edge[i].next)
{
int v = edge[i].to;
dfs(v);
times[u] += times[v];
}
}
注意:是从叶子结点向上 dfs
优化的原理就是省去了我们的代码在树上跳来跳去的情况,相当于将第二幅图中的所有的 0 都直接预先记录 fail 会调到哪里,我们就不用再图上跳来跳去了。