- 进制的表示方法
- 2进制:(0110)B \ or \ 0b0110
- 8进制:(3210)O \ or \ 0o3210
- 10进制:可以直接写数字 or \ (123)D
- 16j进制: (3f3f3f3f)H \ or \ 0x3f3f3f3f
- 原码补码和反码
- 反码 = 原码按位取反。
- 补码 = 原码 - 1
- 前缀编码
- 前缀编码的定义仅当在一组编码中任意一个编码不为另一个编码的前缀
- 哈夫曼编码
- 例如现在有一个集合 \left \{ a,b,c,d,e \right \} 它们出现的概率为 \left \{ 0.1,0.15.0.2,0.25.0.3 \right \}
那么它的哈夫曼编码如下:
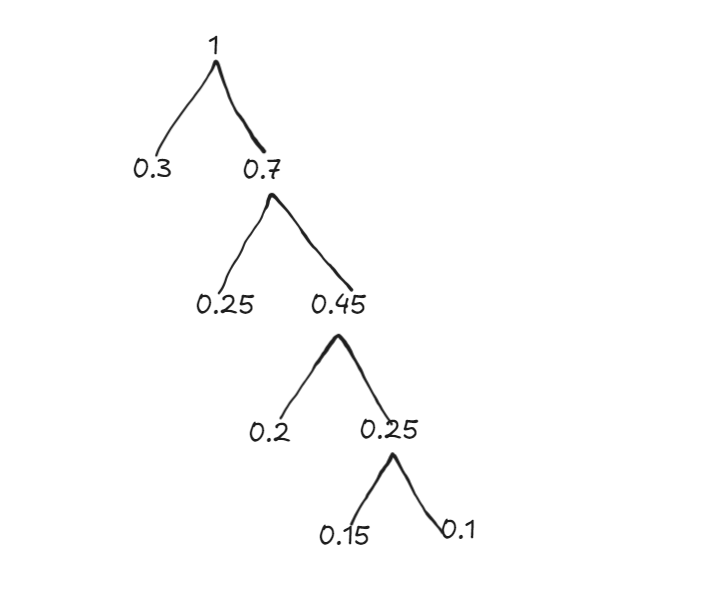
(一般我们把数值小的一方放在右边)
- 二叉树的前序中序和后续遍历
- 前序遍历(NLR) 对于一个节点, 先选根节点,再选左子树,最后选右子树
- 中序遍历(LNR) 对于一个节点, 先选左子树,再选根节点,最后选右子树
- 后序遍历(LRN) 对于一个节点, 先选左子树,再选右子树,最后选根节点
- 组合数学(令种类数为 S )
- 全排列( n 个数 ) S = n \times (n - 1) \times (n - 2) … \times 1
- C_{a}^{b}
(想不出来了,自行补充)
- 时间复杂度计算
用一道题目来代替,答对有赏。
int sum = 0;
for(int i = 1; i < n; i *= 2)
{
for(int j = 0;j < i; j++)
{
sum++;
}
}
问时间复杂度是多少(评论区回答)
- 计算机常识
较长无法列出,这里做举例:
- 计算机之父是图灵
- 冯诺依曼体系
- 信息熵是香农提出的
- ……
宇宙级免责声明
仅代表个人整理知识点(供参考方向复习初赛),不喜勿喷