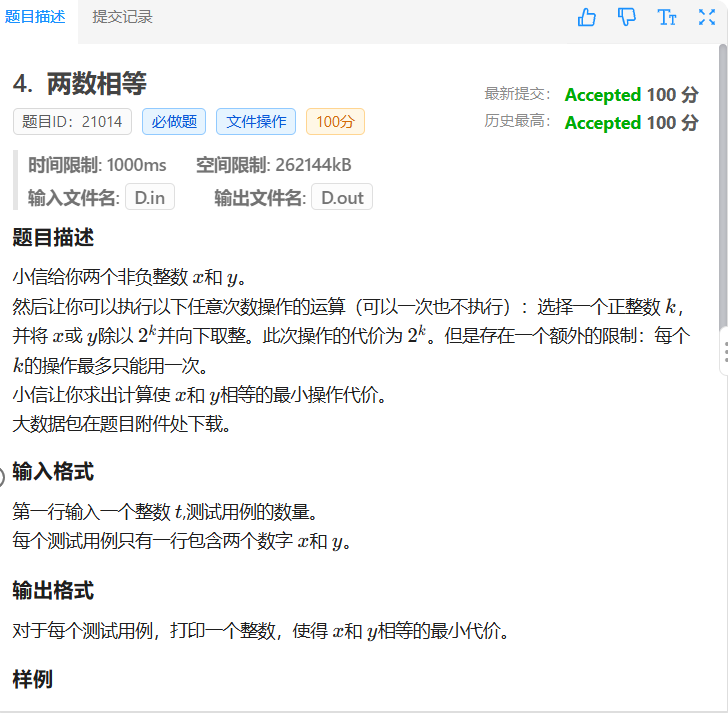
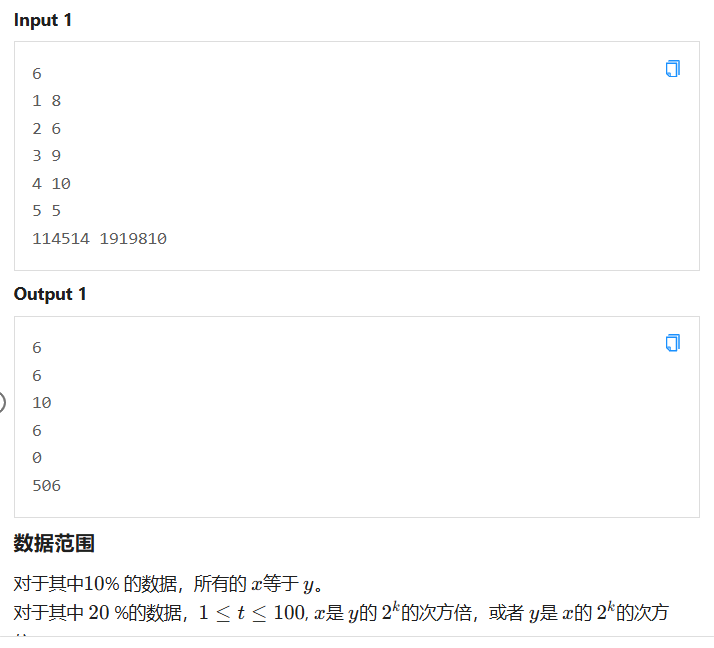

众所周知,老师在课上讲的是01背包做法,此题解没有用半点有关DP的知识
思路
首先我们看两个数x和y
我们可以暴力算出x和y分别至少要除2^sumx和2^sumy才能相等
但是问题是这样代价肯定很高
所以我们先考虑一个数的sum(假设某数要除2^sum次可以达到某个值)
sum=3代价最小为2^1+2^2
我们现在先不看前面这个底数2,看这一坨幂数(3=1+2)
当它可以由1到n组成时最小代价就是n
如果他是1+2+3+4+5+…+n_+x(x<=n)时,利用贪心思想可以从中取出一个数m使x+m=n+1
接下来考虑两个数sum1和sum2
设cnt=sum1+sum2
假如cnt=1+2+3+4+6+7+8
我们可以证明一定有数可以组成sum1,当然剩下的就是sum2
我们可以用一个vector v [120] (因为log2(x,y的范围=1e17)*2约等于114)
来存:
v[3]={1,2} v[11]={1,2,3,5} v[108]={1,2,3,4,5,6,7,8,9,10,11,13,14,15}(应该是这样我可能算错了)
接下来我们就可以用一个ans数组来求代价啦~
用一个deal函数来求ans和v
最后每次输入x,y时只要求出sum=sumx+sumy
再输出ans[sum]就可以了
重要的话说三遍
不开longlong见祖宗
不开longlong见祖宗
不开longlong见祖宗
代码
(就用截图了,以防有人抄)
由于老师要求,代码删了?!
希望大家学习有所成!