DAY9模考总结
题解
T1(调酒大师):

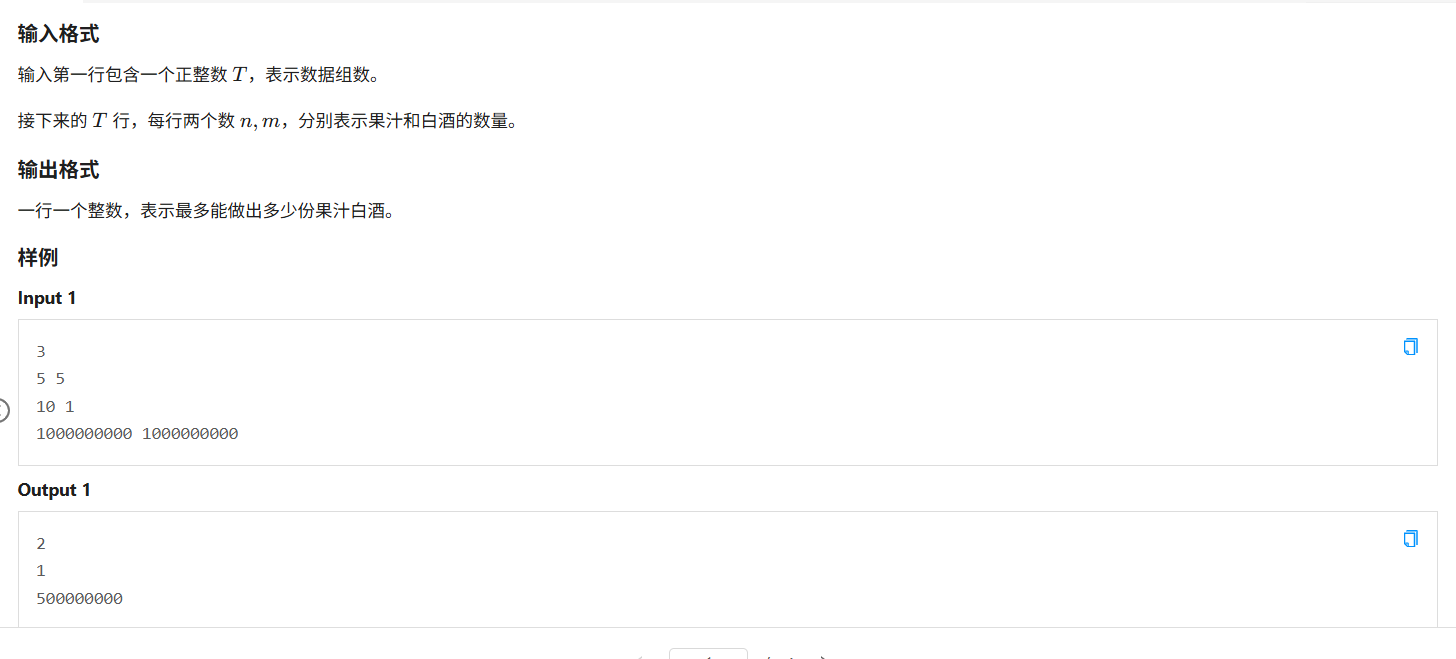
简单的要死,就是需要推理一番,所以。。。。
我们来分析一波!!!
我们最开始想到直接将两种东东直接合在一起然后除以4,但是有些时候并不管用,因为:
![]()
我们其实再加一个限制就可以让他管用,那就是在刚才得出的答案和n、m中选最小,这样可以让我们得出正常的答案
部分代码:
cout << min((n+m)/4, min(n, m)) << endl;
T2(树上最小点覆盖):
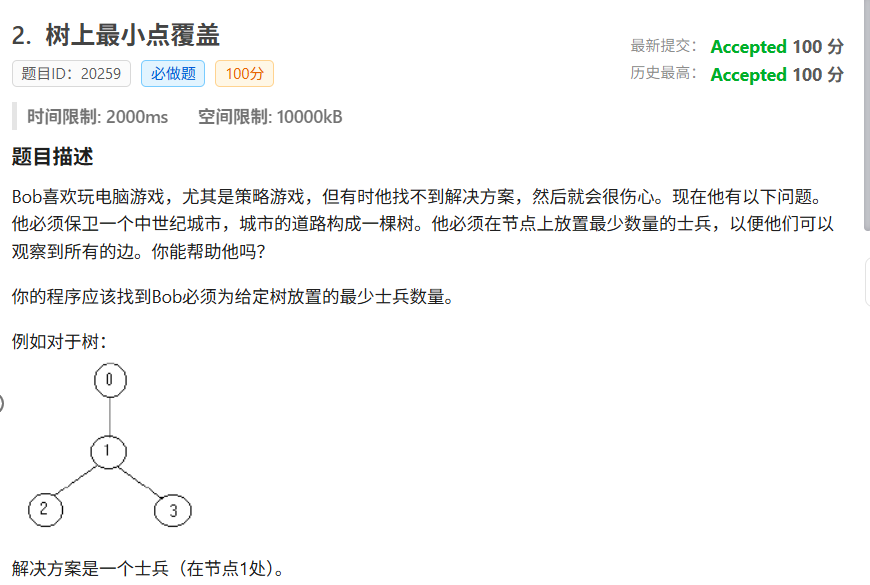

这道题是不是很熟悉??呵呵,还记得我昨天发的总结贴么,没错!!这就是一个树上dp的模版题。(不记得的人回去温习一下!!)
这个dp的状态不算难,就是第一维是当前节点,第二维表示当前节点放不放士兵,正式的来说:
dp_{i,0} 表示以当前节点为根节点,这个点不放士兵,总共需要放多少个士兵才能看见所有的边
dp_{i, 1} 表示以当前节点为根节点,这个点放士兵,总共需要放多少个士兵才能看见所有的边
然后是动态转移方程:
dp_{k, 0}=dp_{k, 0}+dp_{i, 1}
dp_{k, 1}=\min{dp_{i, 1}}, {dp_{i, 1}}
最后输出:
\min{dp_{0, 0}, dp_{0, 1}}
所以接下来是部分代码:
void dfs(ll k, ll f) {
dp[k][0]=0;
dp[k][1]=1;
for (auto i : v[k]) {
if(i==f) continue;
dfs(i, k);
dp[k][0]+=dp[i][1];
dp[k][1]+=min(dp[i][1], dp[i][0]);
}
return;
}
主函数:
while(cin >> n){
for(ll i=0;i<n;i++){
v[i].clear();
}
memset(dp, 0, sizeof(dp));
for(ll i=0;i<n;i++){
ll k, m;
scanf("%d:(%d)", &k, &m);
for(ll i=1;i<=m;i++){
ll a;
cin >> a;
v[k].push_back(a);
v[a].push_back(k);
}
}
dfs(0, -1);
cout << min(dp[0][0], dp[0][1]) << endl;
PS:这里的输入需要用scanf(格式化输入)哟
T3(小信的数学题):

这道题我觉得可以算是全场最难,虽然思路很简单,但是代码很难写且很难调,所以我们主要说一下如何使用代码实现。
基本思路:暴力搜索
代码实现:
我们可以用一个while循环用来枚举每一个出现的字母对应数字的全排列,然后用哈希表对应起来,最后还需要枚举遍历每一个加数,然后按照哈希表将加数加起来,如果这种全排列和正确答案的和相等,我们可以ans++
最后输出ans即可
部分代码:
do {
for (ll i = 0; i < idx; i++) {
cnt[ccnt[i]] = a[i];
}
bool flag = 0;
for (ll i = 1; i <= n; i++) {
if (cnt[s[i][0] - 'A'] == 0) {
flag = 1;
break;
}
}
if (flag) {
continue;
}
ll sum = 0, ans = 0;
for (ll i = 1; i < n; i++) {
ll sum1 = 0;
for (ll j = 0; j < s[i].size(); j++) {
sum1 = sum1 * 10 + cnt[s[i][j] - 'A'];
}
sum += sum1;
}
for (ll j = 0; j < s[n].size(); j++) {
ans = ans * 10 + cnt[s[n][j] - 'A'];
}
if (sum == ans) {
bigAns++;
}
} while (next_permutation(a, a + 10));
PS:这里的全排列函数需要传参数组的开始位置和结束位置
PPS:我们发现写完的代码第二个阳历美国,这是因为事实上输入的字符的种类并不是每一次都是10种,所以我们要用排列组合的知识,最后需要除一个1至没取的的数的阶乘
T4(小信的魔方):
这道题还算简单,只要找到规律就可以找到写法,所以我们需要找一找规律!!
首先我们发现,对于任意两个数,原来在同一行的都在同一行,原来在同一列的都在同一列
所以我们用数组记录下每一行原本的行数和每一列原本的列数,我们只要发现他的列数(行数)变了,我们就给他换到不变为止,这样就可以输出变换的次数,非常简单
部分代码:
ll ans=0;
for(ll i=1;i<=n;i++){
while(b1[i]!=i){
swap(b1[i], b1[b1[i]]);
ans++;
}
}
for(ll j=1;j<=m;j++){
while(b2[j]!=j){
swap(b2[j], b2[b2[j]]);
ans++;
}
}
做题情况
T1:这道题最开始自己推了推,推了个公式出来,结果样例过了,提交!!后面我同桌发现有一个样例过不了,于是我自己又推啊推啊推,我同桌给我的错误样例我就过了,结果我多少分呢?嗯?你猜!你猜!猜不出来吧!
WA 0pt
T2:这道题很难,我搞了半天,认为我的贪心思路是对的,我后桌的同桌 @李予劼 过了,我听他说他没用树形dp,我就更坚定了我的决心,引得 @冯俊骁 来看我的代码,然后我样例过了,你猜我多少分?你猜?你猜?
WA 5pt
T3:这道题直接不管了,我就写了个骗分代码输出1,结果拿了50分!!!
WA 50pt
T4:这道题太难了,我后桌说他过了,我很着急,结果找了半天也没找到规律,结果输出*,可是这个数据太sha*了,所以一分没拿到
WA 0pt
总结
预期得分:220
实际得分:55!!!!!!!!!
这差别也太大了吧!!!!!
太可恶了,我同桌超了我的代码所以他也是55分,我如果在多一些时间去想第一题和第四题的话是有可能AC的!!!还是我太菜了
那就祝我下次模考:
\Huge AK!! 把