本周进行了标准CSP-S组复赛OI模拟赛
得分情况
| 题目 | 做法 | 预计得分 | 实际得分 |
|---|---|---|---|
| A球袋统计 | 标记数组 | 100 | 100 |
| B叁的倍数 | 数学、字符串 | 100 | 100 |
| C小信找硬币 | 搜索、染色、集合 | 0 | 0 |
| D最大复合值 | 背包 | 0 | 0 |
| E曼哈顿多交椭圆 | 前缀和、二分、数学 | 10 | 30 |
A 球袋统计




没想到提高组的题目这么水,心情![]()
直接用标记数组、用cnt统计答案即可(其实这里有个小坑,就是map,因为访问map的时间复杂度是 O(log size) ),大数据会超时,我们还是换成标记数组好
code
#include <bits/stdc++.h>
using namespace std;
int q;
int res[1000010], cnt;
int main() {
cin >> q;
while (q--) {
int op, x;
cin >> op;
if (op == 1) {
cin >> x;
if (res[x] == 0) cnt++;
res[x]++;
} else if (op == 2) {
cin >> x;
if (res[x] == 1) cnt--;
res[x]--;
} else if (op == 3) {
cout << cnt << "\n";
}
}
return 0;
}
B 叁的倍数
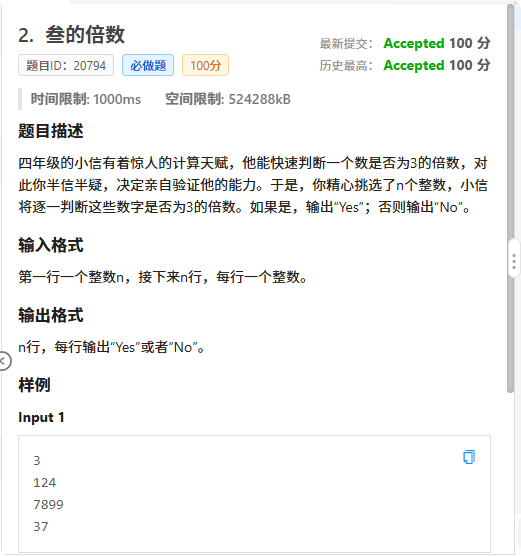

太水了,提高组太水了!![]()
![]()
![]()
学过小学数学的都知道,3的倍数的特征是——所有数位加起来是3的倍数
我们就用字符串存数n,用res来统计数位和,判断res是不是3的倍数即可
code
#include <bits/stdc++.h>
using namespace std;
int n;
string s;
int main() {
cin >> n;
while (n--) {
cin >> s;
int res = 0;
for (int i = 0 ; i < s.size() ; i++) {
res += s[i] - '0';
}
if (res % 3 == 0) {
cout << "Yes\n";
} else {
cout << "No\n";
}
}
return 0;
}
C 小信找硬币

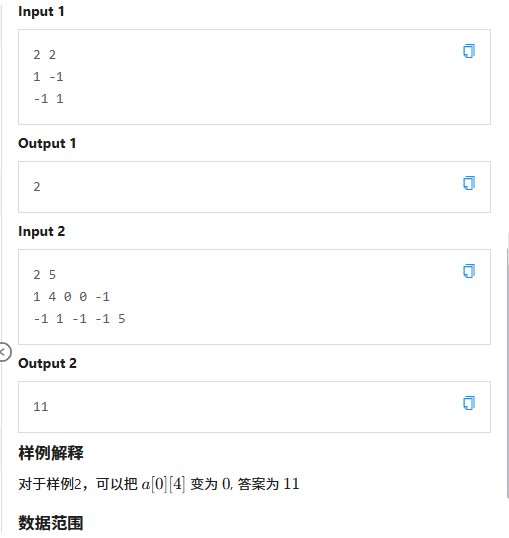
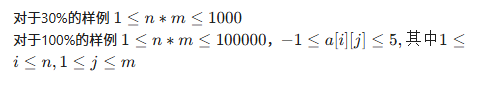
呃,稍微有点水,心情![]()
赛中我脑抽把 n \times m \le10^5 看成了 n,m \le 10^5
所以我就一直想用1维dp做,但是一直做不出来,呜呜呜
正解:
是一个连通块染色,输入完遍历每一个没有被访问并且不是墙的点,随后编号+1,进行染色,在维护一个f数组来存储第编号为i的联通块的钱的总数量
随后遍历每一个墙,把墙的上下左右的染色点的编号装进set里面(因为set可以去重)(如果是墙就不用装),随后把 f[set里的染色编号] 的和打擂台就可以了
(注意,需要特判,万一里面没有墙就没了,所以一开始答案应该是f数组里的最大值)
code
const int dx[] = {-1, 0, 1, 0};
const int dy[] = {0, -1, 0, 1};
vector<vector<int>> a, vis;
vector<int> f;
void dfs(int x, int y, int sum, int& res) {
vis[x][y] = sum;
res += a[x][y];
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if (nx >= 0 && ny >= 0 && nx < n && ny < m && vis[nx][ny] == -1 && a[nx][ny] != -1) {
dfs(nx, ny, sum, res);
}
}
}
int sum = -1;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (a[i][j] != -1 && vis[i][j] == -1) {
sum++;
int res = 0;
dfs(i, j, sum, res);
f.push_back(res);
}
}
}
int ans = 0;
if (!f.empty()) {
ans = *max_element(f.begin(), f.end());
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (a[i][j] == -1) {
set<int> st;
int cnt = 0;
for (int k = 0; k < 4; k++) {
int ni = i + dx[k];
int nj = j + dy[k];
if (ni >= 0 && nj >= 0 && ni < n && nj < m && vis[ni][nj] != -1) {
int tep = vis[ni][nj];
if (st.find(tep) == st.end()) {
st.insert(tep);
cnt += f[tep];
}
}
}
ans = max(ans, cnt);
}
}
}
D 最大复合值

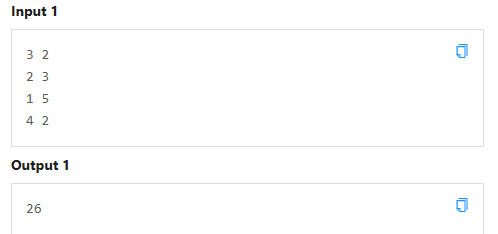

啊怎么能这么难!!!
![]()
![]()
![]()
![]()
![]()
题解:
当固定要在序列 p 中使用的 K 个下标时,序列 p 具有如下性质:
对任意两条线性函数
f_i(x)=A_i x + B_i> f_j(x)=A_j x + B_j
有
f_i\bigl(f_j(x)\bigr)\;>\;f_j\bigl(f_i(x)\bigr) \;\Longleftrightarrow\; \frac{A_i-1}{B_i}\;>\;\frac{A_j-1}{B_j},
并且这一大小关系与 x 无关,只取决于 \tfrac{A_i-1}{B_i} 和 \tfrac{A_j-1}{B_j} 的大小。
因此,当你选定了 K 个下标要插入到 p 中时,为了让
f_{p_1}\bigl(f_{p_2}(\cdots f_{p_K}(1)\cdots)\bigr)
达到最大值,必须让
\frac{A_{p_1}-1}{B_{p_1}} \;\ge\; \frac{A_{p_2}-1}{B_{p_2}} \;\ge\; \cdots \;\ge\; \frac{A_{p_K}-1}{B_{p_K}}.
为简化描述,不妨预先将 (A,B) 对按
\frac{A_1-1}{B_1}\;\ge\;\frac{A_2-1}{B_2}\;\ge\;\cdots\;\ge\;\frac{A_N-1}{B_N}
排序。此时,原问题可等价地表述为:
在区间 \{1,2,\dots,N\} 中选出一个严格增序的长度为 K 的下标序列
1 \le p_1 < p_2 < \cdots < p_K \le N
使得
f_{p_1}\bigl(f_{p_2}(\cdots f_{p_K}(1)\cdots)\bigr)
最大。
这一问题可用下面的动态规划在 O(NK) 时间内求解:
- 定义状态
dp_{i,j} = \max_{\substack{p_{K-i},\dots,p_K \\\text{已选且} \,p_{K-i}\ge j}} f_{p_{K-i}}\bigl(f_{p_{K-i+1}}(\cdots f_{p_K}(1)\cdots)\bigr),
即:在已经决定了末尾 i 个下标,且第 K!-!i 个下标至少为 j 的情况下,所能达到的最大函数值。
2. 转移方程
考虑要不要在位置 j 上选一个下标:
dp_{i,j} = \max\Bigl( dp_{i,j+1}, \;A_j \times dp_{i-1,j+1} + B_j \Bigr).
- 不选 j:保持前面已经选了 i 个下标,最小下标要从 j+1 开始,值为 dp_{i,j+1}。
- 选 j:那就用一次函数 f_j,得到 A_j\cdot(dp_{i-1,j+1})+B_j 。
- 边界条件
dp_{0,j} = 1 \quad(\text{相当于还没应用任何函数时,初始值为 }1).
- 答案
\max_{1\le p_1<\cdots<p_K\le N} f_{p_1}\bigl(f_{p_2}(\cdots f_{p_K}(1)\cdots)\bigr) = dp_{K,1}.
因为状态数是 O(NK),每次转移 O(1),所以总体时间复杂度为 O(NK)。
所以我们只需要先排序,再附初始值,最后状态转移即可
code
bool cmp(pair <ll, ll> x, pair <ll, ll> y) {
return x.first * y.second + x.second < y.first * x.second + y.second;
}
sort(p + 1, p + n + 1, cmp);
for (int i = 0 ; i <= n ; i++) {
dp[i][0] = 1;
}
for (int i = 1 ; i <= n ; i++) {
for (int j = 1 ; j <= k ; j++) {
dp[i][j] = max(dp[i - 1][j], p[i].first * dp[i - 1][j - 1] + p[i].second);
}
}
E 曼哈顿多交椭圆



太难了!!!心情![]()
赛中我输出0居然骗了30分,哈哈哈哈哈哈哈哈
正解:

