
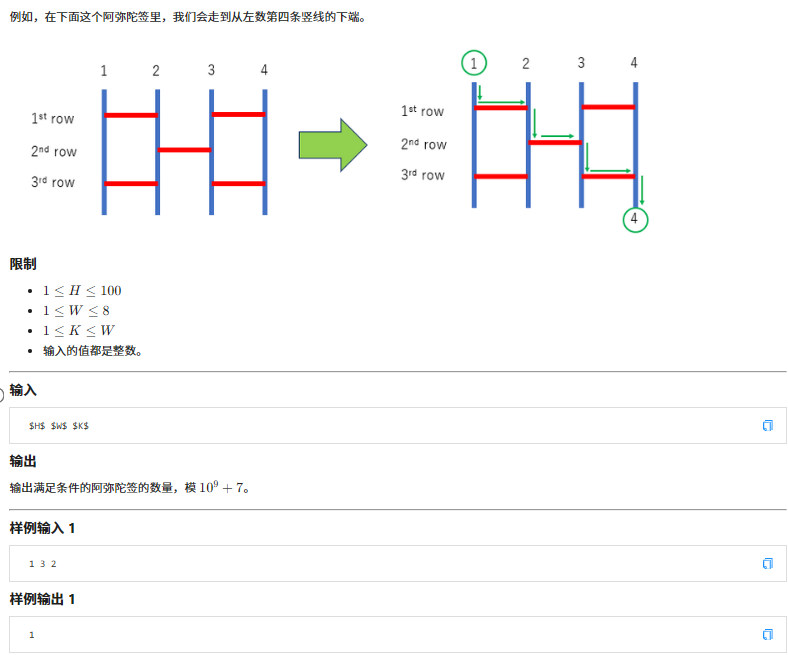
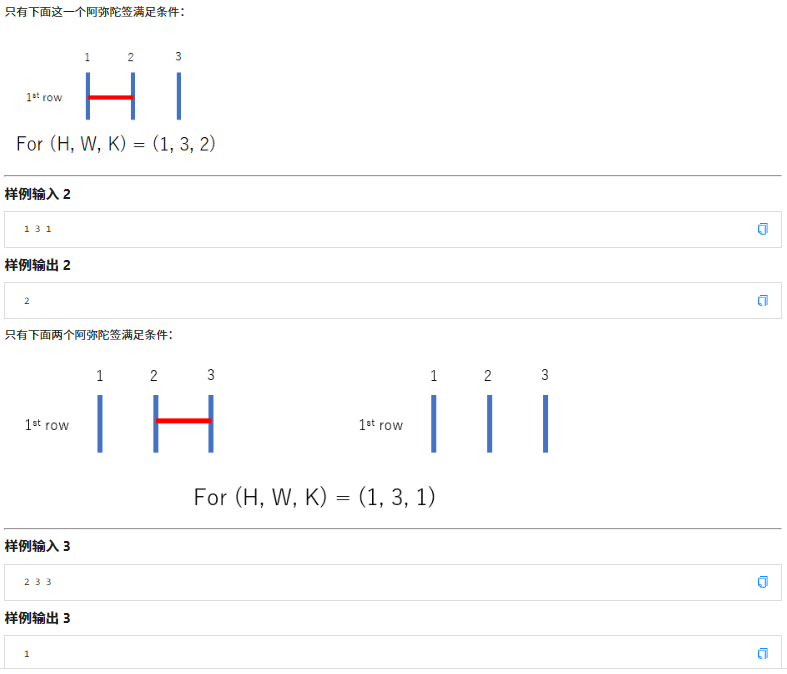
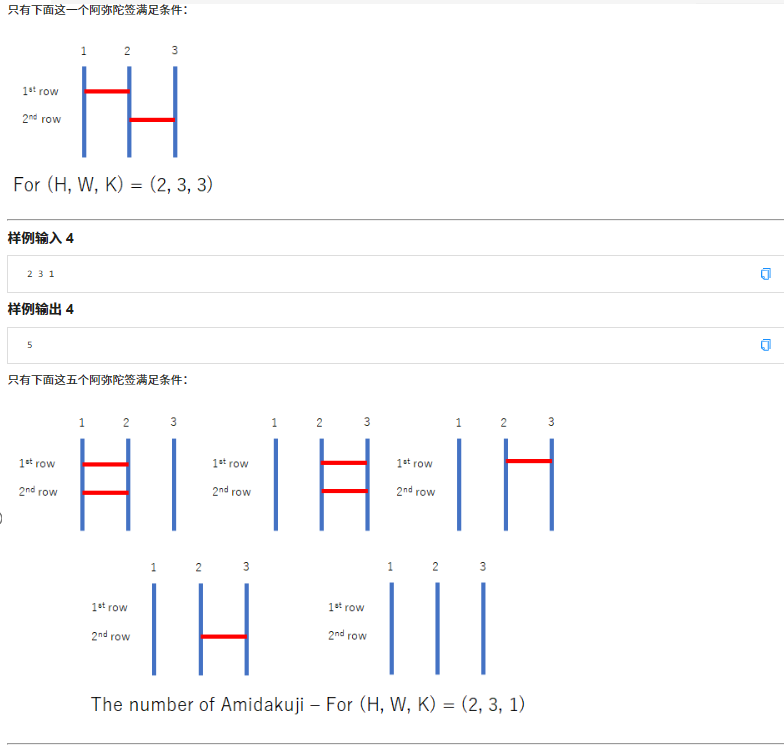

(题目超长的,但是不能怪我
解题思路:
动态规划状态定义
使用二维DP数组:
dp[i][j] 表示处理完前 i 行后,位于第 j 条竖线的方案数
初始:dp[0][1] = 1 (起点在第 1 条竖线)
状态转移设计
枚举所有可能:
用位掩码表示相邻竖线间的连接情况( 1 表示有横线)
例如 W=3 时,可能的布局:00 (无横线)、01 ( 1-2 连接)、10 ( 2-3 连接)
检查位掩码是否有相邻的 1 (就是检查是否有无连续横线)
使用位运算快速判断: j \& (j << 1)
位置计算:
对每个合法布局,计算位置如何变化
有横线连接的相邻位置会交换
更新状态:
根据当前位置和横线布局,更新下一行的可能位置
状态转移方程:dp[i+1][new] += dp[i][now]
时间复杂度:O(H × 2^W × W)
空间复杂度:O(H × W)
接下来献上我写了两年半的代码
解题伪代码:
#include <bits/stdc++.h>
#define I using
#define AK namespace
#define IOI std
#define i_ak return
#define ioi 0
#define i_will signed
#define ak main
#define IMO ()
#define int long long
#define double long double //别问我为什么这么像WYC的,问就是我抄他的
I AK IOI;
const int MOD = 1e9 + 7;
inline int read(){ //我有快读你有吗
int x = 0, c = getchar(), sign = 1;
while(c < '0' || c > '9') {
if(c == '-') sign = -1;
c = getchar();
}
while(c >= '0' && c <= '9') {
x = x * 10 + (c - '0');
c = getchar();
}
return x;
}
i_will ak IMO {
ios::sync_with_stdio(false);cin.tie();
int H = read(), W = read(), K = read();
vector<vector<int>> dp(H + 1, vector<int>(W + 2, 0)); // 表示处理完前i行后位于第j条竖线的方案数
// 初始状态:0行处理后位于第1条竖线
// 动态规划处理每一行
for (int i = 0; i < H; ++i) { // 枚举所有可能的横线连接方式(用位掩码表示)
for (int j = 0; j < (1 << (W - 1)); ++j) { // 检查当前横线布局是否合法(没有相邻的横线)
bool vis = true;
for (int k = 0; k < W - 2; ++k)
if ((j & (1 << k)) && (j & (1 << (k + 1)))) {
vis = false;
break;
}
if () continue; // 跳过非法布局
int t[W + 1]; // 在当前横线布局下,在第i根竖线会到第T[i]根竖线上
for (int k = 1; k <= W; ++k) ; // 初始化:默认位置不变
// 交换相邻位置
for (int k = 0; k < W - 1; ++k)
if () { // 如果第k和第k+1条竖线之间有横线
// 位置转移
}
// 更新
for (int k = 1; k <= W; ++k) dp[i + 1][t[k]] = (dp[i + 1][t[k]] + dp[i][k]) % MOD;
}
}
// 输出
i_ak ioi; // 相当于 return 0;
}
好了,题解结束了,是不是很水 (不过该有的都有了(bushi
完结撒花 ✿✿ヽ(°▽°)ノ✿