本周进行了标准OI模考
得分情况
| 题目 | 做法 | 预计得分 | 实际得分 |
|---|---|---|---|
| A小信爱音游 | 循环结构 | 100 | 70 |
| B寻找等边三角形 | 循环结构、哈希表 | 0 | 0 |
| C小信学习欧几里得算法 | 数学、素数筛、前缀和 | 0 | 0 |
| D小信的生产线 | set集合 | 0 | 0 |
A-小信爱音游


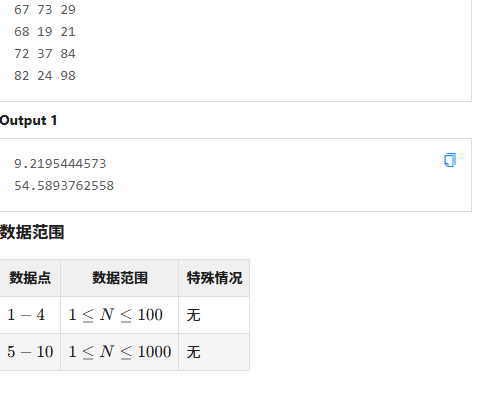
超级简单的啦,只需要按他说的做,计算得数打擂台就好了
可惜我![]() 输出总是自动保留小数气死我了,调了42分钟才调对输出
输出总是自动保留小数气死我了,调了42分钟才调对输出
本来我能一百的但是我心想:是不是可以用longdouble?
于是我手欠加了一个longdouble,结果从AC变成了WA70
呜呜呜呜呜
code
struct node {
double t, x, y;
};
node a[1010];
for (int i = 1 ; i <= n ; i++) {
double dx = abs(a[i].x - a[i + 1].x) * 1.0;
double dy = abs(a[i].y - a[i + 1].y) * 1.0;
res = max(res, sqrt(dx * dx + dy * dy) / abs(a[i + 1].t - a[i].t));
}
B- 寻找等边三角形

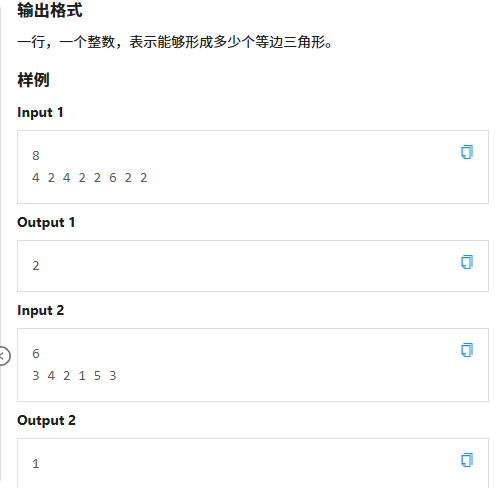

比赛里我看这个数组是距离与下一个的,不好计算
我写了一遍TLE,接着改成RE,又变成CE,最后直接变成WA,我差点红温而死
正解:用map来存储圆上面每个位置有没有点
接着遍历每个点,由于是等边三角形,所以它的边长(底)肯定是圆的周长的三分之一,靠着这个原理我们就寻找另外两个位置看看有没有点,有的话就res(answer)++
code
map <int, bool> mp;
for (int i = 1 ; i <= n ; i++) {
sum += a[i];
}
sum /= 3;
for (int i = 2 ; i <= n ; i++) {
b[i] = b[i - 1] + a[i - 1];
mp[b[i]] = 1;
}
for (int i = 1 ; i <= n ; i++) {
if (mp[b[i] + sum] && mp[b[i] + sum * 2]) res++;
}
C- 小信学习欧几里得算法
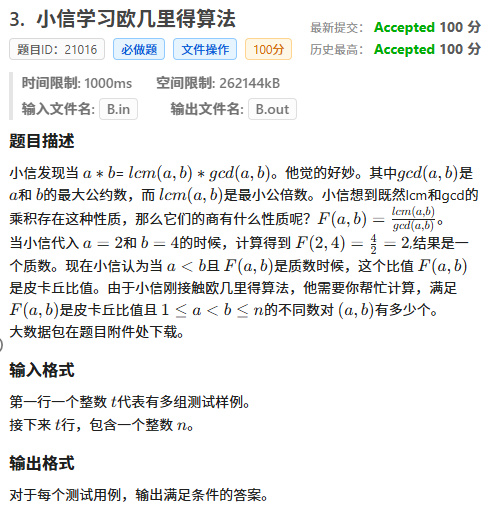

我们先简单证明一下:只有b是a的素数倍,F(a,b)才是皮卡丘:
我们需要证明以下命题:
对于正整数 a 和 b,如果 a<b 且 gcd(a,b)lcm(a,b) 是一个素数,那么 b 必须是 a 的素数倍。
换句话说,我们需要证明: gcd(a,b)lcm(a,b) 是素数 ⟹b=a⋅p 其中 p 是素数
预备知识
-
最大公因数(gcd)和最小公倍数(lcm)的关系: 对于任意正整数 a 和 b,有: lcm(a,b)⋅gcd(a,b)=a⋅b 因此: gcd(a,b)lcm(a,b)=(gcd(a,b))2a⋅b
-
设 d=gcd(a,b): 令 a=d⋅m 和 b=d⋅n,其中 gcd(m,n)=1(因为 d 是最大公因数)。 那么: gcd(a,b)lcm(a,b)=d2a⋅b=d2dm⋅dn=mn 因此: mn 是素数
证明过程
- 从 mn 是素数出发:
-
素数的定义是大于1的自然数,且只有1和它本身两个正约数。
-
因此 mn 是素数意味着 m 和 n 中一个是1,另一个是素数(因为 gcd(m,n)=1 排除了其他可能性)。
- 分析 a<b:
-
由 a=dm 和 b=dn,且 a<b,有 m<n。
-
因为 mn 是素数,且 m<n,所以:
-
m=1
-
n 是素数。
-
- 推导 b 和 a 的关系:
-
由 m=1 和 n 是素数:
-
a=d⋅1=d
-
b=d⋅n
-
-
因此: b=a⋅n 其中 n 是素数。
- 验证:
-
如果 b=a⋅p(p 是素数),则:
-
gcd(a,b)=gcd(a,ap)=a
-
lcm(a,b)=lcm(a,ap)=ap
-
因此: gcd(a,b)lcm(a,b)=aap=p 这是一个素数。
-
结论
我们证明了: gcd(a,b)lcm(a,b) 是素数 ⟹b=a⋅p 其中 p 是素数 且反过来也成立。因此命题得证。
好了,这就是证明,这样我们就可以开始了
先埃氏筛或欧拉筛一下,中途+一下答案数组f的值
最后求一下f的前缀和即可
code
for (int i = 2 ; i <= 10000000 ; i++) {
if (!vis[i]) {
f[i]++;
for (int j = i * 2 ; j <= 10000000 ; j += i) {
vis[j] = 1;
f[j]++;
}
}
}
for (int i = 1 ; i <= 10000000 ; i++) {
f[i] += f[i - 1];
}
D- 小信的生产线

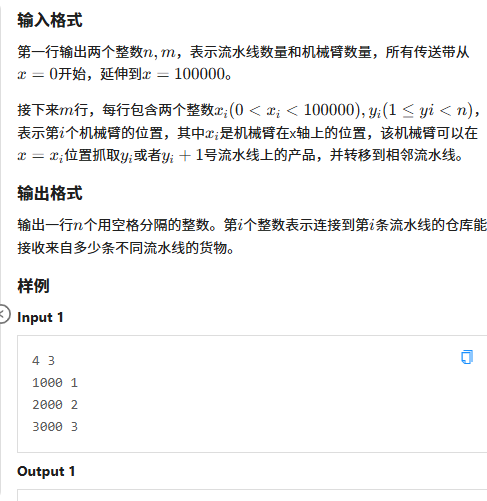
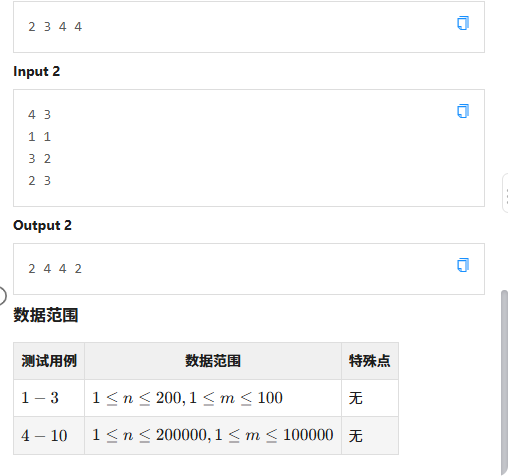
看似是一个有向图的遍历,实际上并不是,我们想一想如果把所有机械臂按位置升序排序,那么我们就可以直接遍历每个机械臂,因为机械臂可以互换物品,我们就可以把两边的物品各在另一边也放上
(每个物品用其原来的传送带编号命名)
但是我们也会发现问题:这样输出就不好做,而且还会有重复的物品上来
比如一个机械臂两边都有物品d,那么d就又被分配到了两边,这会导致不必要的重复
我们有两种解决方案:
- 用vector数组,可以用find函数来判断是否重复从而手动去重,输出的时候也只需要输出size即可
- 用set,set可以自动去重,也有size的函数,不需要复杂的手动去重,只要insert即可
code
struct node {
int x, y;
}a[100010];
set <int> st[200010];
bool cmp(node c, node d) {
return c.x < d.x;
}
sort(a + 1, a + m + 1, cmp);
for (int i = 1 ; i <= n ; i++) {
st[i].insert(i);
}
for (int i = 1 ; i <= m ; i++) {
for (auto it : st[a[i].y]) {
st[a[i].y + 1].insert(it);
}
for (auto it : st[a[i].y + 1]) {
st[a[i].y].insert(it);
}
}
