
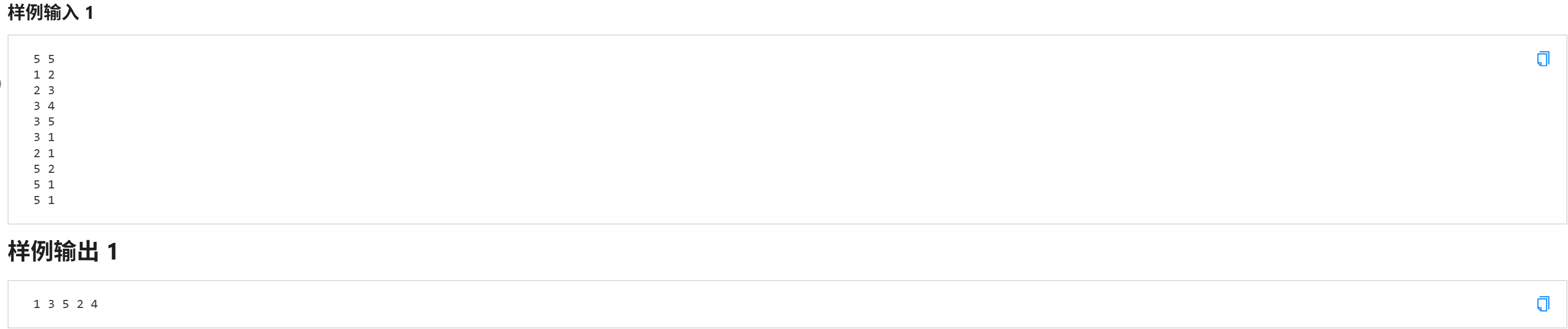
题目大意: 给你一棵 n 个节点的树和 m 个炸弹,第 i 个炸弹在节点 p_i 的位置,爆炸范围是 w_i 。炸弹 i 爆炸后会波及到距离不超过 w_i 的节点。求每一个节点会被多少个炸弹波及。
具体思路:首先,我们可以考虑一个这道题目的简化版:炸弹只能往后代炸。这时候,我们可以记 f[i][j] 表示传递到节点 i 后还有多余波及距离 j 的炸弹数。这个数组的递推式是:
f[s][j] = f[s][j]+f[i][j+1],s\in son[i]
然后,我们可以考虑给炸弹几个分身,也就是给有根树上炸弹节点的祖先再添加 1 个范围是当前范围 -1 的炸弹。但是,我们会发现,这样会使部分节点出现多余的炸弹。这时候,我们可以想到,只要让冲突节点对应的下标提前减一就可以刚好抵消,这样既可以正常传递炸弹,又不怕重复出现本来是同一个的“假炸弹”。这样就通过了本题。
参考代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll N = 5e5 + 5;
vector<ll> b[N], g[N];
vector<ll> b2[N];
ll f[N][105], fa[N];
ll n, m;
void dfs(ll u, ll ff)
{
fa[u] = ff;
for (ll w : b[u])
{
ll t = u, t2 = w;
f[t][t2]++;
t2--;
while (t != 1 && t2 >= 0)
{
if (t2 > 0) f[t][t2 - 1]--;
f[fa[t]][t2]++;
// b2[t].push_back(-t2 - 1);
// b2[fa[t]].push_back(t2);
t = fa[t];
t2--;
}
}
for (ll v : g[u])
{
if (ff == v) continue ;
dfs(v, u);
}
}
void dfs2(ll u, ll fa)
{
for (int i = 1; i <= 50; i++)
{
for (ll v : g[u])
{
if (v != fa)
{
f[v][i - 1] += f[u][i];
}
}
}
for (ll v : g[u])
{
if (v == fa) continue ;
dfs2(v, u);
}
}
int main()
{
// freopen(".in", "r", stdin);
// freopen(".out", "w", stdout);
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
for (int i = 2; i <= n; i++)
{
ll u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
for (int i = 1; i <= m; i++)
{
ll p, w;
cin >> p >> w;
b[p].push_back(w);
}
dfs(1, 0);
dfs2(1, 0);
for (int i = 1; i <= n; i++)
{
ll ans = 0;
for (int j = 0; j <= 50; j++)
{
ans += f[i][j];
}
cout << ans << '\n';
}
return 0;
}