分治
分治( Divide and Conquer )是一种把大问题拆成小问题、再合并结果的思路。在C++语境下,它更像是一种“解题心法”,而不是某个具体语法。
可以这样理解它:
-
拆:把当前问题的规模缩小,通常拆成两个或更多“子问题”,这些子问题和原问题长得一样,只是规模更小。
-
治:对每个子问题,继续用同样的方法去拆,直到规模小到一眼就能看出答案。
-
合:把每个子问题的答案按规则拼起来,得到原问题的答案。
拿生活中的例子类比:
- 你要统计全校学生的平均分。如果人数太多,你就把全校按班级拆成若干子问题;每个班再拆成小组;小组人数足够少时,直接算平均分;最后把各组、各班的平均分按人数加权合并,就得到全校的平均分。
C++里常见的场景:
-
排序:把大数组拆成两半分别排序,再合并两个有序数组。
-
求最大子段和:把数组拆成左右两半,最大和要么在左半边、要么在右半边、要么跨越中间,分别算再取最值。
-
平面最近点对:把所有点按x坐标拆成两半,分别找左右最近的点对,再检查中间“带状区域”是否有更近的点。
核心思路就一句:大问题不会直接硬算,而是不断“拆小→算小→拼答案”,让复杂度从“一口吃成胖子”变成“分而食之”。
分治之归并排序
归并排序就是“分治版排序”的典范:
-
把数组平分成两半;
-
对两半分别递归排序;
-
把两个已排好序的子数组合并成一个有序数组。
下面是简洁的代码:
code
#include <bits/stdc++.h>
using namespace std;
int n;
int a[1000010];
int tmp[1000010];
void sum(int a[], int l, int mid, int r) {
int i = l, j = mid + 1, k = l;
while (i <= mid && j <= r) {
if (a[i] < a[j]) {
tmp[k++] = a[i++];
} else {
tmp[k++] = a[j++];
}
}
while (i <= mid) tmp[k++] = a[i++];
while (j <= r) tmp[k++] = a[j++];
for (int i = l ; i <= r ; i++) a[i] = tmp[i];
}
void f(int a[], int l, int r) {
if (l >= r) {
return;
}
int mid = (l + r) / 2;
f(a, l, mid);
f(a, mid + 1, r);
sum(a, l, mid, r);
}
int main() {
cin >> n;
for (int i = 1 ; i <= n ; i++) {
cin >> a[i];
}
f(a, 1, n);
for (int i = 1 ; i <= n ; i++) {
cout << a[i] << " ";
}
return 0;
}
归并排序=“分治三部曲”的教科书式示范。下面把思路拆成五个关键词讲透,不贴代码,纯聊逻辑。
-
递归结构
把“排序长度为n的数组”抽象成“排序任意区间[l,r)”。只要区间长度>1,就永远切成两半 (mid=(l+r)/2),左右各自递归。递归出口是区间长度≤1,天然有序。
2.心法:相信递归——左右两半递归返回时一定已经排好序,你只需要专心“合并”。 -
合并(Merge)
合并是归并排序唯一“干活”的阶段。想象两条已排好序的扑克牌列,每次翻开头一张比大小,把较小的牌放到结果堆里。因为两列都有序,所以每次翻出的牌一定是当前全局最小。
4.技巧:
-
合并时只需一次线性扫描, O(n) 。
-
合并完把结果写回原区间,上层递归继续用。
-
稳定排序
合并时“相等元素取左边”保证原相对顺序不变,因此归并排序天生稳定。这在需要保留原始顺序的场景(如多关键字排序)很关键。 -
复杂度剖析
-
分治树高度:log2 n 层。
-
每层合并总代价:O(n)。
-
整体时间复杂度:O(n log n),最坏、平均、最好都一样。
-
额外空间:需要临时数组,O(n)。代价换稳定与最坏性能保证。
- 拓展应用
归并排序的“分治+合并”框架能套到很多统计问题:
-
逆序对数量:合并时发现“右边元素比左边小”即产生逆序对,计数即可。
-
区间和问题:合并时顺带维护前缀和。
-
外部排序:数据太大放不进内存,用归并思想多路合并磁盘文件。
一句话总结:
归并排序把“排序”拆成“排左边+排右边+合并”,递归地让复杂度从 O(n^2) 降到 O(n log n),而合并阶段又能顺手完成各种统计任务,所以既是排序算法,也是分治模板。
归并之逆序对
逆序对($Inversion Pair$)是一个“顺序被颠倒”的索引二元组。
把数组下标也写出来就一目了然:
对于数组 A[0 … n-1],如果存在 i < j 且 A[i] > A[j],那么 (i, j) 就是一个逆序对。
1. 直观例子
索引: 0 1 2 3 4
数值: 2 4 1 3 5
-
(0,2) 是逆序对,因为 2 > 1 且 0 < 2
-
(1,2) 是逆序对,因为 4 > 1 且 1 < 2
-
(1,3) 是逆序对,因为 4 > 3 且 1 < 3
其余组合都满足 i<j 时 A[i]≤A[j],不算。
2. 为什么关心逆序对
-
数组 已经有序 ⇔ 逆序对数量为 0。
-
逆序对数量越大,数组越“乱”。
-
在排序、推荐系统、基因序列比对、Kendall Tau 距离等领域,它被当成“乱序度量”。
3. 如何高效计数
暴力双重循环 O(n^2) 太慢。
借助 归并排序的分治框架 可以做到 O(n log n):
思路回顾:
归并排序在合并两个已排好序的子数组时,左右指针 从左到右扫描。
当右指针指向的元素被选中(因为它更小)时,左指针左边剩余的所有元素 都与当前右元素构成逆序对。
于是合并阶段顺带统计即可,不额外增加复杂度。
4. 一句话总结
逆序对就是“前面大、后面小”的索引对;归并排序的合并步骤天然适合一次性数完它们。
实现统计数组逆序对计数的简介代码
code
#include <bits/stdc++.h>
using namespace std;
long long n, ans;
int a[100010];
int tmp[100010];
void sum(int a[], int l, int mid, int r) {
int i = l, j = mid + 1, k = l;
while (i <= mid && j <= r) {
if (a[i] < a[j]) {
tmp[k++] = a[i++];
} else {
tmp[k++] = a[j++], ans += mid - i + 1;
}
}
while (i <= mid) tmp[k++] = a[i++];
while (j <= r) tmp[k++] = a[j++];
for (int i = l ; i <= r ; i++) a[i] = tmp[i];
}
void f(int a[], int l, int r) {
if (l >= r) {
return;
}
int mid = (l + r) / 2;
f(a, l, mid);
f(a, mid + 1, r);
sum(a, l, mid, r);
}
int main() {
cin >> n;
for (int i = 1 ; i <= n ; i++) {
cin >> a[i];
}
f(a, 1, n);
cout << ans << "\n";
return 0;
}
经典例题
P1309 [NOIP 2011 普及组] 瑞士轮
题目背景
在双人对决的竞技性比赛,如乒乓球、羽毛球、国际象棋中,最常见的赛制是淘汰赛和循环赛。前者的特点是比赛场数少,每场都紧张刺激,但偶然性较高。后者的特点是较为公平,偶然性较低,但比赛过程往往十分冗长。
本题中介绍的瑞士轮赛制,因最早使用于 1895 年在瑞士举办的国际象棋比赛而得名。它可以看作是淘汰赛与循环赛的折中,既保证了比赛的稳定性,又能使赛程不至于过长。
题目描述
2 \times N 名编号为 1\sim 2\times N 的选手共进行 R 轮比赛。每轮比赛开始前,以及所有比赛结束后,都会按照总分从高到低对选手进行一次排名。选手的总分为第一轮开始前的初始分数加上已参加过的所有比赛的得分和。总分相同的,约定编号较小的选手排名靠前。
每轮比赛的对阵安排与该轮比赛开始前的排名有关:第 1 名和第 2 名、第 3 名和第 4 名、……、第 2\times K - 1 名和第 2\times K 名、…… 、第 2\times N - 1 名和第 2\times N 名,各进行一场比赛。每场比赛胜者得 1 分,负者得 0 分。也就是说除了首轮以外,其它轮比赛的安排均不能事先确定,而是要取决于选手在之前比赛中的表现。
现给定每个选手的初始分数及其实力值,试计算在 R 轮比赛过后,排名第 Q 的选手编号是多少。我们假设选手的实力值两两不同,且每场比赛中实力值较高的总能获胜。
输入格式
第一行是三个正整数 N,R,Q,每两个数之间用一个空格隔开,表示有 2\times N 名选手、R 轮比赛,以及我们关心的名次 Q。
第二行是 2\times N 个非负整数 s_1, s_2,\dots, s_{2\times N},每两个数之间用一个空格隔开,其中 s_i 表示编号为 i 的选手的初始分数。
第三行是 2\times N 个正整数 w_1,w_2,\dots,w_{2\times N},每两个数之间用一个空格隔开,其中 w_i 表示编号为 i 的选手的实力值。
输出格式
一个整数,即 R 轮比赛结束后,排名第 Q 的选手的编号。
输入输出样例 #1
输入 #1
2 4 2
7 6 6 7
10 5 20 15
输出 #1
1
说明/提示
【样例解释】
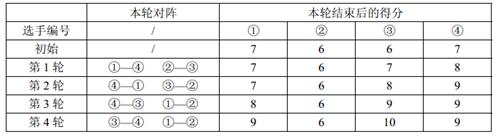
【数据范围】
对于 30\% 的数据,1\le N\le 100;
对于 50\% 的数据,1\le N\le 10000;
对于 100\% 的数据,1\le N\le 10^5,1\le R\le 50,1\le Q\le 2\times N,0\le s_1, s_2,\dots,s_{2\times N}\le 10^8,1\le w_1, w_2 , \dots, w_{2\times N}\le 10^8。
noip2011 普及组第 3 题。
code
#include <bits/stdc++.h>
using namespace std;
struct node {
int s, ww, id;
} a[200005], w[200001], l[200001];
bool cmp(node x, node y) {
if (x.s != y.s) return x.s > y.s;
else return x.id < y.id;
}
int n, r, q;
int main() {
cin >> n >> r >> q;
for (int i = 1 ; i <= 2 * n ; i++) {
cin >> a[i].s, a[i].id = i;
}
for (int i = 1 ; i <= 2 * n ; i++) {
cin >> a[i].ww;
}
sort(a + 1, a + 2 * n + 1, cmp);
for (int i = 1 ; i <= r ; i++) {
int sum = 0, cnt = 0;
for (int j = 1 ; j <= 2 * n ; j = j + 2) {
if (a[j].ww > a[j + 1].ww) w[++cnt] = a[j], l[++sum] = a[j + 1], w[cnt].s++;
else l[++sum] = a[j], w[++cnt] = a[j + 1], w[cnt].s++;
}
merge(w + 1, w + 1 + cnt, l + 1, l + 1 + sum, a + 1, cmp);
}
cout << a[q].id << "\n";
return 0;
}
前缀和与差分进阶
由于此知识点过于基础,请不懂的同学上网自行搜索
我讲解一些例题
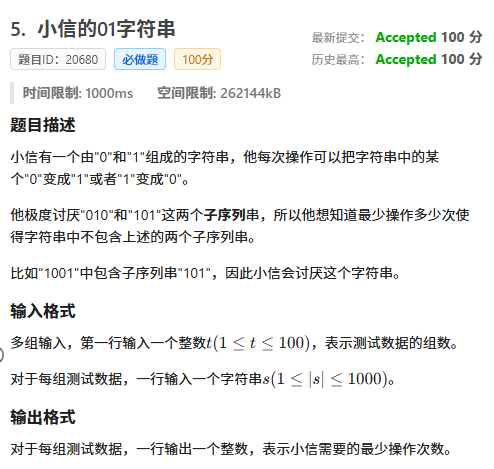
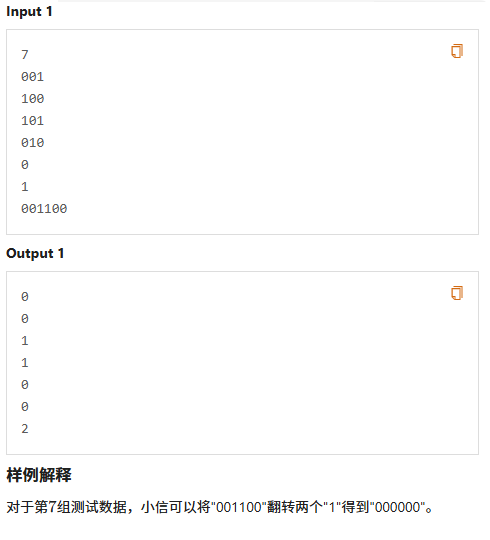
通过读题我们发现,如果中间有1,0就只能在左边或右边,而且不能左右都有
同理,如果中间有0,1就只能在左边或右边,而且不能左右都有
那么就只有4种情况
- 全部是1
- 全部是0
- 左边都是0,右边都是1
- 左边都是1,右边都是0
那么我们就可以遍历每一个点,选择把它左边都变成0、右边都变成1或者左边都变成1,右边都变成0
code
int res = 0x3f3f3f3f;
memset(a, 0, sizeof(a));
cin >> s;
int n = s.size();
s = ' ' + s;
for (int i = 1 ; i <= n ; i++) {
a[i] = a[i - 1] + (s[i] - '0');
}
for (int i = 1 ; i <= n ; i++) {
res = min(res, i - 1 - a[i - 1] + (a[n] - a[i]));
res = min(res, a[i - 1] + (n - i + 1) - (a[n] - a[i - 1]));
}
cout << res << "\n";
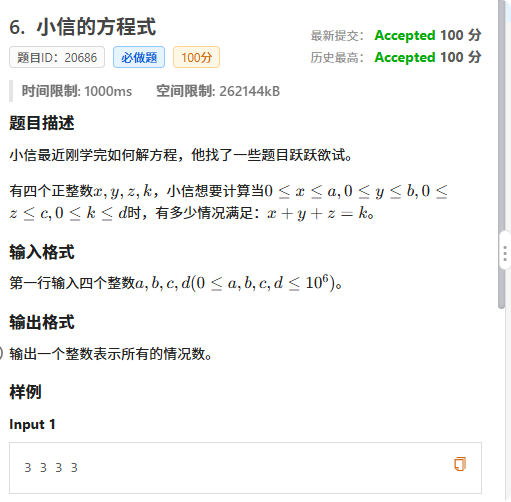
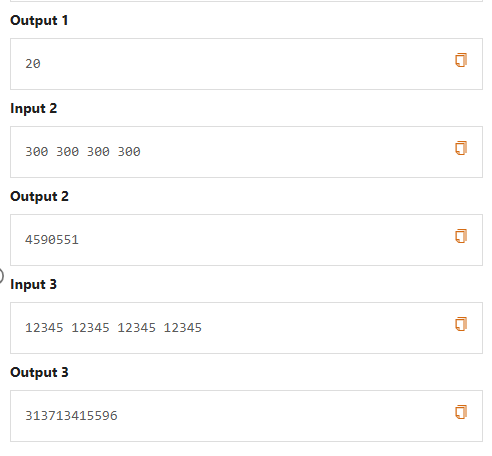
这道题目我们暴力做法是三重循环遍历abc
但是我们可以用差分的思想来做这道题目
首先求出a+b等于i的情况数
接着把a+b看做一个整体
再用差分数组求出a+b+c=i的方案数
接着输出 ans_d 即可
code
for (int i = 0 ; i <= a ; i++) {
dif[i]++;
dif[i + b + 1]--;
}
for (int i = 1 ; i <= a + b ; i++) {
dif[i] = dif[i] + dif[i - 1];
}
for (int i = 0 ; i <= a + b ; i++) {
dif2[i] += dif[i];
dif2[i + c + 1] -= dif[i];
}
for (int i = 1 ; i <= a + b + c ; i++) {
dif2[i] = dif2[i] + dif2[i - 1];
}
for (int i = 0 ; i <= d ; i++) res += dif2[i];
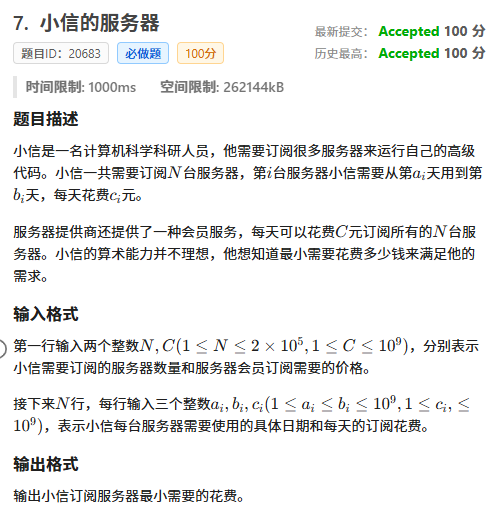
思路其实很容易想到,但是这个使用天数有可能是1e9,数组根本存不下,而且会超时
这时候我们就要用map当做差分数组
随后我们每次统计一个键值对到下一个键的花费,看看要不要开通会员
code
map <int, long long> mp;
cin >> n >> VIP;
for (int i = 1 ; i <= n ; i++) {
cin >> a >> b >> c;
mp[a] += c;
mp[b + 1] -= c;
}
long long pre = 0;
long long sum = 0;
for (auto [x, w] : mp) {
res += min(sum, VIP) * (x - pre);
sum += w;
pre = x;
}