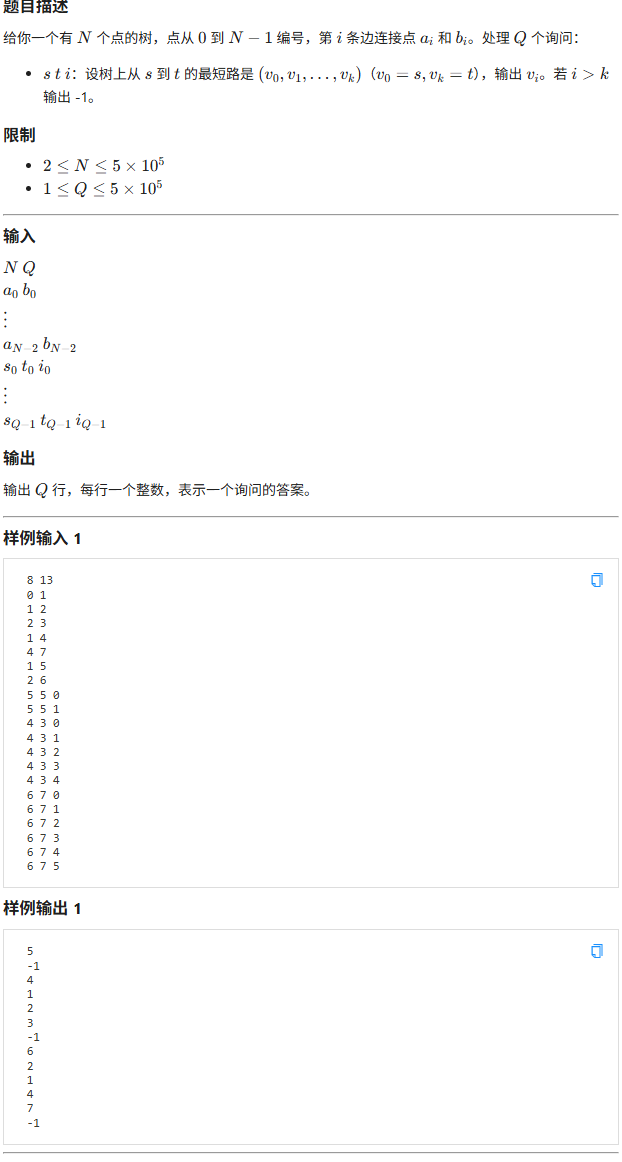
题目描述
思路
题目给了一棵树
并询问 u 到 v 的最短路径的第 k 步是哪个节点
突破口 是树上最短路径
考虑使用树上倍增求LCA
倍增数组求完LCA后还可以用来算第 k 步位于哪个节点,一举两得
注意 处理第 k 步时要分情况讨论
-
- 第 k 步在 u ~ LCA(u,v) 之间,那么从 u 点向上跳
-
- 第 k 步在 v ~ LCA(u,v) 之间,那么从 v 点向上跳
预处理倍增数组
void dfsinit(int now, int fa)
{
dep[now] = dep[fa]+1;
for(int i = 0; i<20; i++)
{
bz[now][i+1] = bz[bz[now][i]][i];
}
for(int i = 0; i<vec[now].size(); i++)
{
int v = vec[now][i];
if(v!=fa)
{
bz[v][0] = now;
dfsinit(v,now);
}
}
}
倍增求LCA
int lca(int u, int v)
{
if(dep[u]<dep[v])
{
swap(u,v);
}
for(int i = 20; i>=0; i--)
{
if(dep[bz[u][i]]>=dep[v])
{
u = bz[u][i];
}
}
if(u == v)
{
return u;
}
for(int i = 20; i>=0; i--)
{
if(bz[u][i]!=bz[v][i])
{
u = bz[u][i];
v = bz[v][i];
}
}
return bz[u][0];
}
查询
for(int i = 1; i<=m; i++)
{
int u;
int v;
int x;
cin>>u>>v>>x;
u++;
v++;
int tmp = lca(u,v);
int res = 0;
if(x>(dep[u]+dep[v]-2*dep[tmp])){
cout<<"-1\n";
continue;
}
if(x<=dep[u]-dep[tmp]){
res = u;
for(int i = 20; i>=0; i--){
if(x>=(1<<i)){
res = bz[res][i];
x-=(1<<i);
}
}
}
else{
x = dep[u]+dep[v]-2*dep[tmp]-x;
res = v;
for(int i = 20; i>=0; i--){
if(x>=(1<<i)){
res = bz[res][i];
x-=(1<<i);
}
}
}
cout<<res-1<<'\n';
}