本周进行了标准模考训练
得分情况:
| 题目 | 算法 | 预计得分 | 实际得分 |
|---|---|---|---|
| A田忌赛马 | 分支结构 | 100 | 100 |
| B地精的金币 | 数学、字符串、计数思想 | 100 | 100 |
| C数矩形 | 二分、前缀和 | 0 | 0 |
| D小信打扑克 | 贪心、全排列 | 0 | 0 |
题目解析
A 田忌赛马
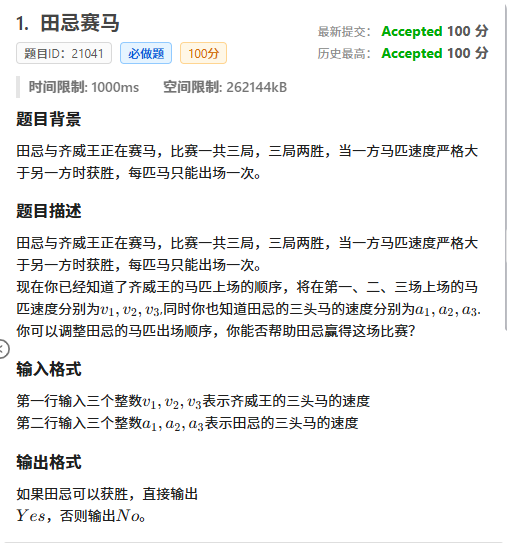

呃~,非常简单的一道模拟题
通过田忌赛马的思路来写(有点废话)
用下等马对上等马、上等马对中等马、中等马对下等马
首先排个序,接着看一下孙膑的思路能不能赢就好了
不过这里有一个坑点:题目问的是能不能赢,而不是谁赢,所以就算平局也算输
code
#include <bits/stdc++.h>
using namespace std;
int a[4], b[4];
bool check() {
int win = 0;
if (a[3] < b[1]) win++;
if (a[2] < b[3]) win++;
if (a[1] < b[2]) win++;
return win >= 2;
}
int main() {
for (int i = 1 ; i <= 3 ; i++) {
cin >> a[i];
}
for (int i = 1 ; i <= 3 ; i++) {
cin >> b[i];
}
sort(a + 1, a + 3 + 1);
sort(b + 1, b + 3 + 1);
if (check()) {
cout << "Yes\n";
} else {
cout << "No\n";
}
return 0;
}
B 地精的金币

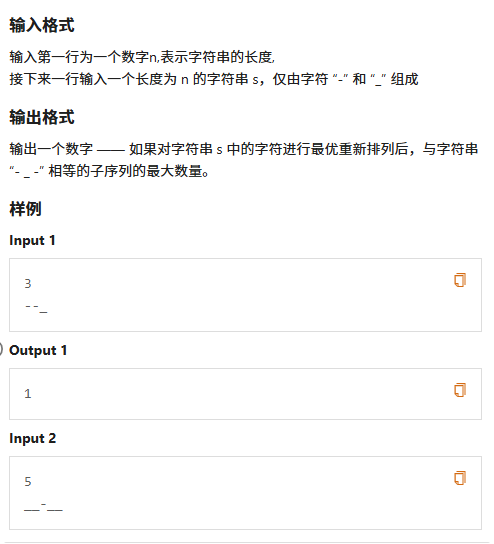
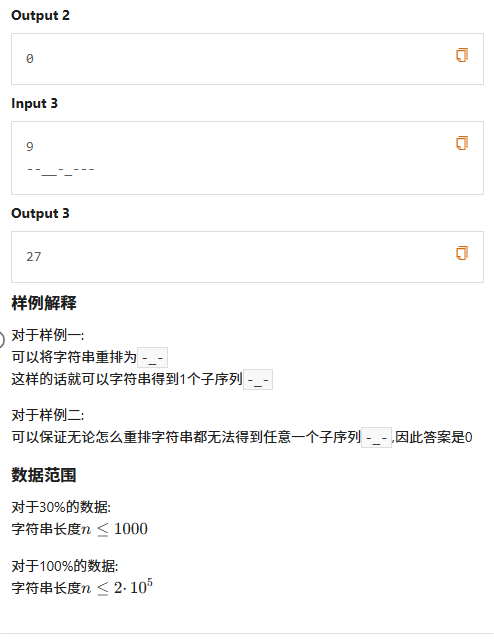
嗯,题目读懂了就会做了,思路是把所有眼睛均匀放到两边,中间放嘴巴
那么通过十分简单的数学推演我们得到
(sum1为眼睛个数,sum2为嘴巴个数)
answer=\frac{sum1}{2}\times \frac{sum1 + 1}{2}\times sum2
code
#include <bits/stdc++.h>
using namespace std;
int n;
string s;
int main() {
cin >> n >> s;
long long sum1 = 0/*-*/, sum2 = 0/*_*/;
for (int i = 0 ; i < n ; i++) {
if (s[i] == '-') sum1++;
else sum2++;
}
long long ans = ((sum1 + 1) / 2) * (sum1 / 2) * sum2;
cout << ans << "\n";
return 0;
}
C 数矩形


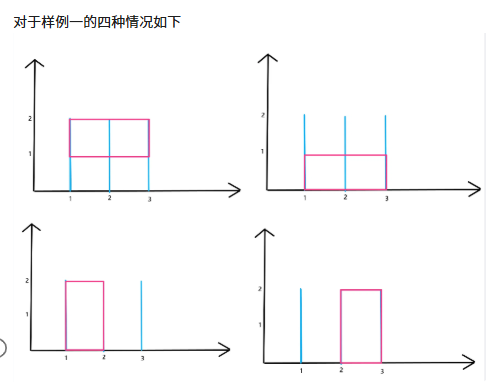

这题我比赛时写暴力,结果样例都没过,所以没有提交
题目题解:

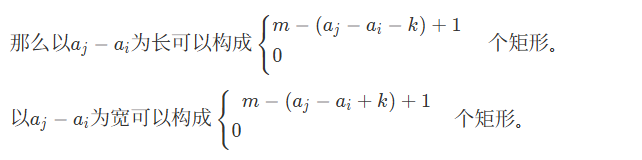
那么答案就是



卖个关子,读完题目我的第一个问题不是怎么做,而是,为什么是“x,c,a,m,p”这几种花色,后来我想了半天终于想到了“X-camp”就是花色字母的来源
本来我不会做,后来我发现其实可以用最长上升子序列的dp思路来做,但是后来发现这样会TLE,而且很麻烦,我写完代码还样例不过,弄了半天也没好,所以就没有提交
这个写的详细了一点
题目理解
我们需要将小信手中的扑克牌整理成特定的顺序:同一花色的牌必须按编号升序排列,且王牌花色(X)必须出现在所有其他花色之后。每次操作可以选择一张牌抽出并插入到任意位置,求最少需要多少次操作才能完成整理。
关键点
- 目标序列:同一花色的牌按编号升序排列,且所有X牌必须出现在最后。
- 操作定义:每次操作可以移动一张牌到任意位置。
- 最少操作次数:即通过最少的移动次数将当前序列整理为目标序列。
解题思路
- 目标序列的构造:
- 将非王牌花色(C, A, M, P)的牌按花色分组,每组内按编号升序排列。
- 将王牌花色(X)的牌按编号升序排列,并放在所有非王牌花色之后。
- 最少操作次数的计算:
- 最少操作次数等于当前序列中未被正确排序的牌的数量。具体来说,是当前序列中未被包含在目标序列的最长递增子序列(LIS)中的牌的数量。
- 因此,最少操作次数 = 总牌数 - 目标序列的最长递增子序列的长度。
- 具体步骤:
- 将输入序列转换为目标序列。
- 计算当前序列与目标序列的最长公共子序列(LCS)的长度。
- 最少操作次数 = 总牌数 - LCS长度。
示例分析
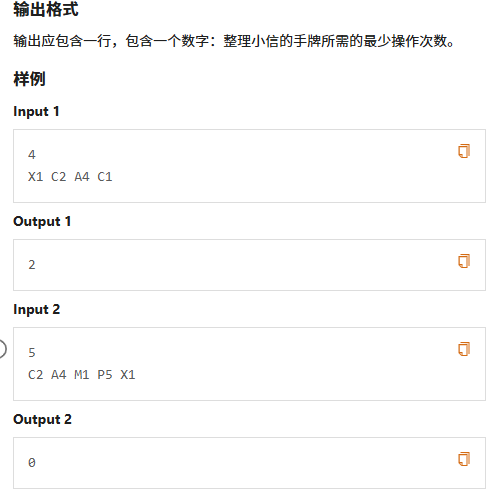
- 样例1:
- 输入序列:X1, C2, A4, C1
- 目标序列:C1, C2, A4, X1
- LCS(按顺序匹配):C2, A4(长度为2)
- 最少操作次数 = 4 - 2 = 2
- 样例2:
- 输入序列:C2, A4, N1, P5, X1
- 目标序列:C2, A4, N1, P5, X1(假设N为普通花色)
- LCS:整个序列(长度为5)
- 最少操作次数 = 5 - 5 = 0(但输出为8,可能题目描述有误或输入描述不完整)
注意事项
- 需要正确处理花色的优先级(X最后,其他花色按输入顺序或字母顺序排列)。
- 确保目标序列的构造与题目要求一致。
- 使用高效的LCS算法(如基于动态规划或贪心的优化方法)以处理大规模数据。
总结
通过构造目标序列并计算当前序列与目标序列的最长公共子序列,可以高效地求出最少操作次数。关键在于正确理解目标序列的构造规则和操作的定义。
总总总总结
这次比赛虽然分数相比上次提高了,但是我好像并没有什么进步的
而俗话说得好,学习如逆水行舟,不进则退
所以我这次应该退步了
反思:我拿暴力部分分的能里不够强