前言
本蒟蒻的第一篇题解,这题在给出思路的前提下难度并不高,但代码相当复杂
本人做了三天

分析
我们可以先将命题转化为一个简单的模型:小Z初始能力值为a[1],每遍历一个点,能力值增加A,其他点的点权增加B,当能力值>a[i]的点权时,a[i]能被遍历
求从a[1]到a[n]最少需要遍历的点的数量
也就是说在限制条件下,求出a[1]到a[n]的最短路,那么这题所用的核心算法就很明确了:
dijsktra!
但是维护不断变化的能力值和点权非常复杂,因此我们实际上可以求出
从a[1]到a[i]的需遍历的点数的限制
分三种情况讨论:
- A>B,此时对于每个点,都能求出到达该点最少需要遍历的点数
- A==B,此时相当于该命题无需考虑增量变为一道简单的最短路问题,使用bfs或dijkstra即可解决
- A<B,此时对于每个点,都能求出到达该点最多可以遍历的点数(因为当遍历到一定点数时,原本可达的点的点权大于了能力值,变得不可达了)
直接贴代码吧
for(int i=2;i<=n;i++){
tim[i]=0;
if(a==b){
if(c[i]>=c[1])tim[i]=1;
else tim[i]=INT_MAX;//要么随时可达,要么永远不可达
}else if(a>b){
//能够到达该点的最早时间
if(c[i]>=c[1]){
tim[i]=(c[i]-c[1])/(a-b)+((c[i]-c[1])`%`(a-b)!=0)+1;
//最少时间为总差值除以每一步的增量,向上取整
}else{
tim[i]=1;//若起始能力值就大于点权则一开始就可达
}
}else{
//能够到达该点的最晚时间,与最早时间同理
if(c[i]>c[1]){
tim[i]=-1;
}else{
tim[i]=(c[1]-c[i])/(b-a)+((c[1]-c[i])%(b-a)!=0)+1;
}
}
}
于是你直接按时间的限制打出了边权为一的dijsktra,样例都没过
这是为什么呢?
题目中,小Z为了尽可能走到a[n]处,是会走多余的路的,但是dijsktra算法是不走多余路的,举个简单的例子:
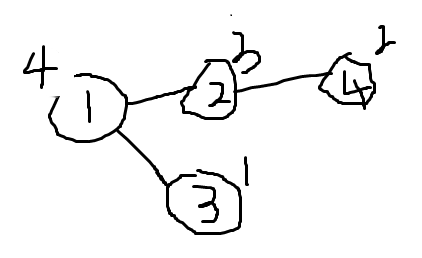
在这组样例中,若A=3,B=2,则在搜索的过程中无法达到点2,但实际上通过先到3,再到2的方式是能够搜到n的
PS:在题面描述中,点权先增大,能力值再增大,因此第一天时a[1]=4,a[2]=5,不可达
因此我们需要找到一种方法,统计出每个点是否可达
我们发现如果只考虑每个点是否可达,则先走所需时间少的一定不会劣(证明略
于是,我们可以使用优先队列,按照所需时间长短排序,依次进行遍历,直到不可达为止
(此情况只适用于A>=B,因为在A<B时一定不会走多余的路,证明略(A==B时可统计出所有可达的点))
#define dis first
#define p second
int nowt=0;
for(int i=1;i<=n;i++)vis2[i]=0;
priority_queue<pair<int,int> ,vector<pair<int,int> >,greater<pair<int,int> > > to;
//按每个到达的最少击败人数排序(即最早时间
for(auto it:t[1]){
int pn=it.p;
to.push({tim[pn],pn});
}
vis2[1]=1;
while(to.size()){
int u=to.top().p;
to.pop();
if(nowt+1>=tim[u]&&vis2[u]==0){
//如果到达时击败的人数大于需要击败的人数,则将与u有关的点都进入
vis2[u]=1;//标记一下可达的点
for(auto it:t[u]){
int pn=it.p;
to.push({tim[pn],pn});
}
nowt++;
}else if(nowt+1<tim[u]){
//由于按照需要击败的人数排序,因此只要有一个点无法到达,则后面的点都不可能到达
return;
}
}
这样,我们的代码就基本完成了,只需要在dijsktra找最短路的同时判断该点是否可达即可
解释有点难,还是看代码吧
for(int i=1;i<=n;i++)vis[i]=0;
priority_queue<pair<int,int> ,vector<pair<int,int> >,greater<pair<int,int> > > pq;
dis[1]=0;
pq.push({dis[1],1});//push起点
int nowt=0;
while(!pq.empty()){
int u=pq.top().p;
pq.pop();
if(vis[u])continue;
vis[u]=1;
for(auto it:t[u]){
int d=it.dis,pn=it.p;
int w=d+dis[u];//从上一个点直接到该点的时间
if(a>=b){
if(vis2[pn])w=max(w,tim[pn]);
//取w与能够到达该点的最早时间的较大值,如果w>=tim[pn]说明到达该点至少需要走w的时间
//若w<tim[pn]说明到达该点时能力值依然小于最快时间,需要走多余的路将时间补到最少时间
else continue;
}
if(a<b&&w>=tim[pn]){
//w>=tim[pn]说明该点点权已经大于能力值,不可能再到达
continue;
}
if(w>dis[pn])continue;
dis[pn]=w;
pq.push({dis[pn],pn});//这里就是标准的dijsktra了
}
}
写完才发现这题用bfs应该也能做