题面
意思大概是两只青蛙在一条直线上做往返运动,问它们相遇了几次?
思路
参考过以前的题解,发现没有讲的很清楚,所以特写此篇:
首先,一看到题目,本来以为很简单的,但仔细看看发现并不是我想的那样。
40pts做法
只需要考虑 V1, V2 两者有一者为 0 的情况和 V1 = V2 的情况,这时候,只需要考虑相遇的情况即可。不需要考虑追及的情况。我们简单推理发现:当往返**1,3,5……**次的时候会相遇(如果 V1 = V2 那么将 V1 变成 2 \times V1, V2 = 0 就可以了)
核心代码:
if(V1 == V2 || V1 == 0 || V2 == 0)
{
V1 = V2 + V1;
V2 = 0;
long long ans = V1 * T / L;
cout << (ans + 1) / 2;
}
100pts 做法
100pts的做法个人认为这个确实挺难的,要想好久。
首先我们先考虑相遇的情况:
我们可以轻易的得到:公式为:\frac{L}{V1 + V2} (为a)
然后我们在考虑追及的情况:
然后我们也可以轻易的得到:公式为:\frac{L}{V1 - V2} (为b)
当然没有结束,当我们胸有成竹的输出 a + b 的时候,发现除了那40pts之外全都是WA。
为什么呢。我们简单的画一个图:
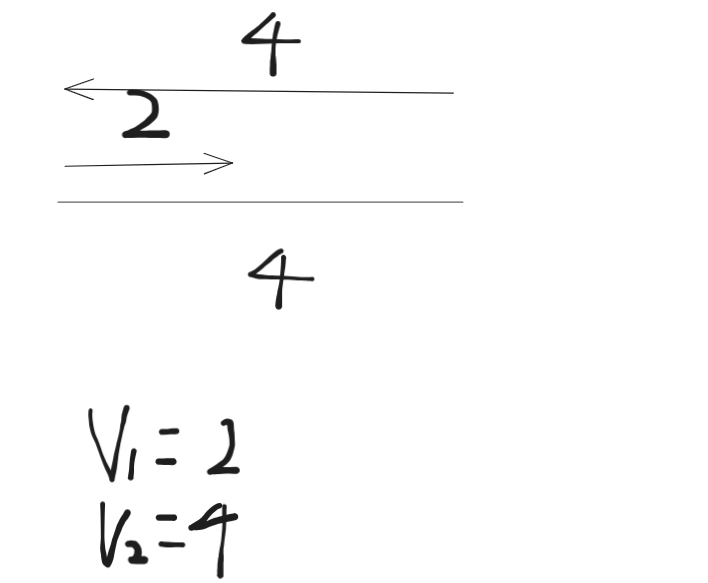
我们简单手推,发现在2s之后,他们全都在最右边的端点。
现在,在这种情况下,我们的计算机就会把这种情况当成追及和相遇的情况一起,这样,明明只有一种相遇的时候,硬是被算成了两次。
所以,我们现在的任务是找到他们一共重复了多少次,
我们可以转化成他们经过了几个大周期。
现在,我们定义 t = lcm(\frac{L}{V1},\frac{L}{V2}) = \frac{L}{gcd(V1,V2)}
cnt_1 = \frac{V1}{gcd(V1,V2)}
cnt_2 = \frac{V2}{gcd(V1,V2)}
可以得到次数 k = \frac{gcd(V1, V2)T-L}{2L}
最后,我们可以对$cnt_1,cnt_2$进行奇偶判断,如果 cnt_1 + cnt_2 \mod 2 = 1
那么 ans = a + b - k
否则 ans = a + b
本帖结束
