求解方程！！！

常规
1

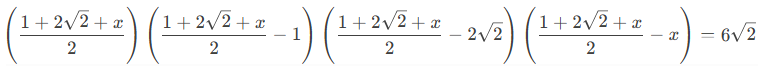
image
RT,给Deepseek+元宝给干沉默了，所以求解

2 个赞
2

x=1+2\sqrt{2} \pm 2\sqrt{1+\sqrt{2}}

—来自deepseek解答

1 个赞
3

image
此方程无解

1 个赞
4

（帖子已被作者删除）

5

（帖子已被作者删除）

6

（帖子已被作者删除）

7

原方程：

(\frac{1+2\times\sqrt{2}+x}{2})\times(\frac{1+2\times\sqrt{2}+x}{2}-2\times\sqrt{2})\times(\frac{1+2\times\sqrt{2}+x}{2}-x)=6\times\sqrt{2}

把原方程改为函数形式，求y=0时的x值

y=(\frac{1+2\times\sqrt{2}+x}{2})\times(\frac{1+2\times\sqrt{2}+x}{2}-2\times\sqrt{2})\times(\frac{1+2\times\sqrt{2}+x}{2}-x)-6\times\sqrt{2}

放入函数计算器

算出的函数长这样
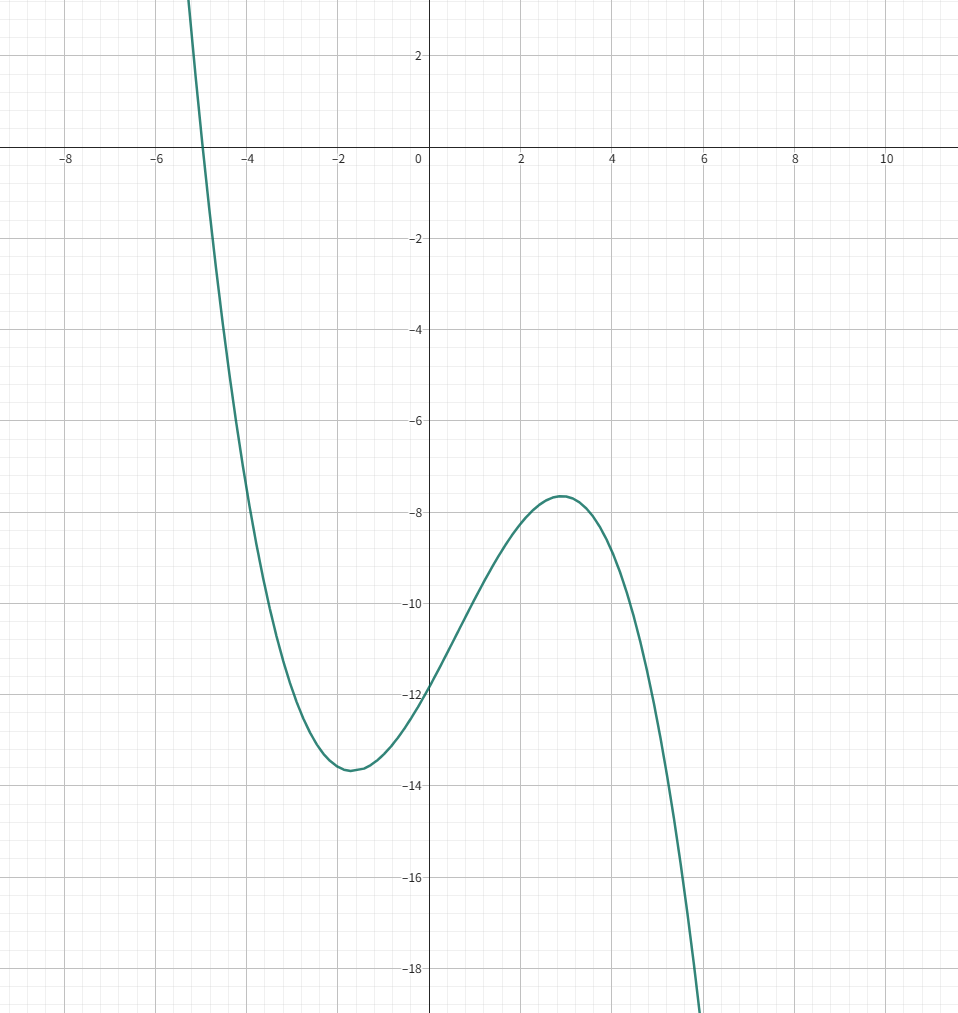
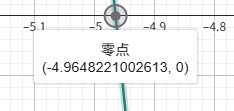
image
image
so，x约为-4.9648221002613
写题解写一半跑偏了

1 个赞
8

乐，我就知道哪来这么简单答案

3 个赞
9

用 AI 还想要解决方案？

1 个赞
10

@yhxyd0104
《答案是2》
怎么可能！

1 个赞
11

你这个方程就抄错了
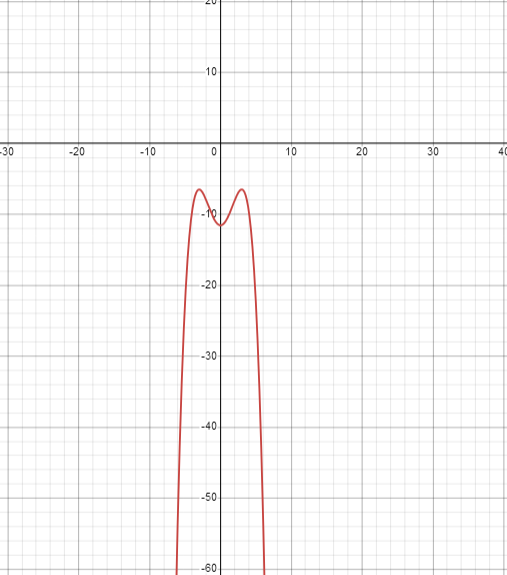
按照函数图像来说
令 y=\left(\frac{1+2\sqrt{2}+x}{2}\right)\left(\frac{1+2\sqrt{2}+x}{2}-1\right)\left(\frac{1+2\sqrt{2}+x}{2}-2\sqrt{2}\right)\left(\frac{1+2\sqrt{2}+x}{2}-x\right)-6\sqrt{2}
当且仅当 y=0 时原方程才会等于 6\sqrt{2}
所以我们可以得到
image
欸~ ( *^-^)
原方程无实数解

2 个赞
12

你这个属于是提 \frac{1}{2} 就提错了
对于
\left(\frac{1+2\sqrt{2}+x}{2}-1\right)
提完后应该是
\left(\frac{2\sqrt{2}+x-1}{2}\right)

2 个赞
13

（帖子已被作者删除）

14

（帖子已被作者删除）

15

@yhxyd0109 确实，我少抄了一个项

原方程：

(\frac{1+2\times\sqrt{2}+x}{2})\times(\frac{1+2\times\sqrt{2}+x}{2}-1)\times(\frac{1+2\times\sqrt{2}+x}{2}-2\times\sqrt{2})\times(\frac{1+2\times\sqrt{2}+x}{2}-x)=6\times\sqrt{2}

把原方程改为函数形式，求y=0时的x值

y=(\frac{1+2\times\sqrt{2}+x}{2})\times(\frac{1+2\times\sqrt{2}+x}{2}-1)\times(\frac{1+2\times\sqrt{2}+x}{2}-2\times\sqrt{2})\times(\frac{1+2\times\sqrt{2}+x}{2}-x)-6\times\sqrt{2}

放入函数计算器

算出的函数长这样
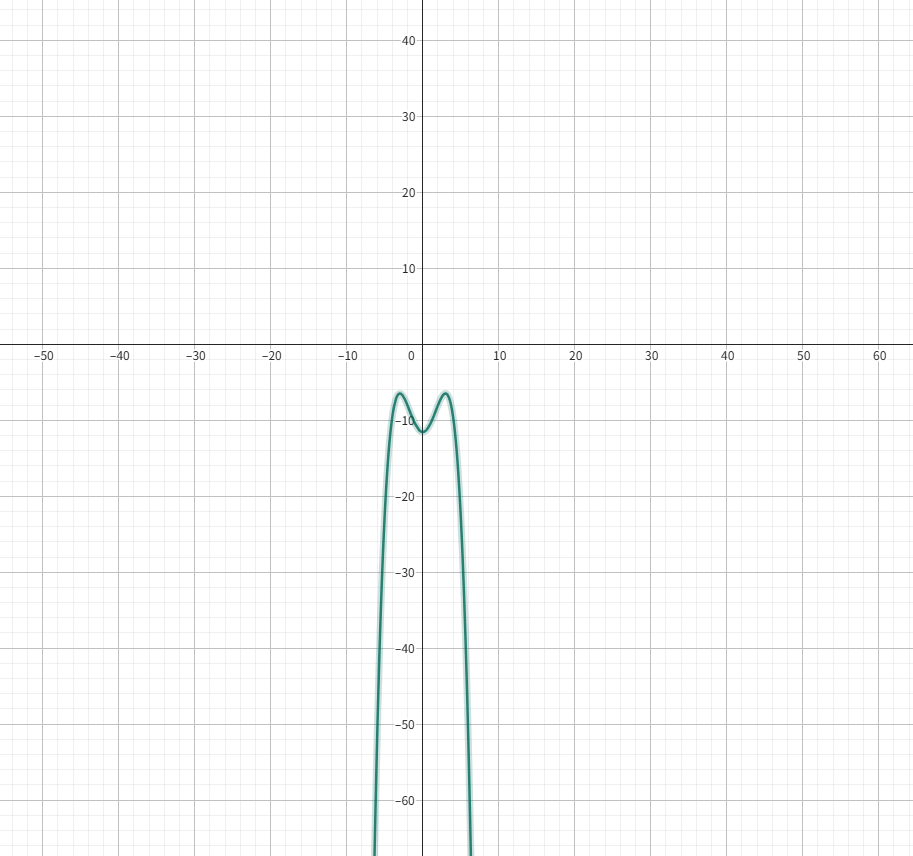
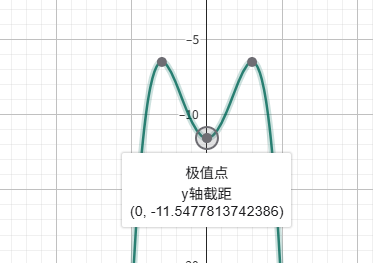
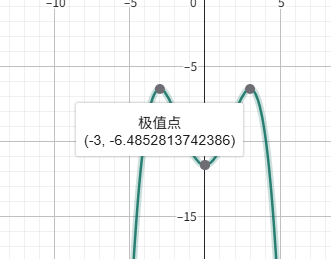
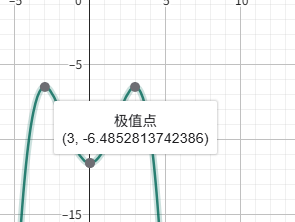
image
image
image
image
so，原方程无实根
\LaTeX 的方程源码：

$$
(\frac{1+2\times\sqrt{2}+x}{2})\times(\frac{1+2\times\sqrt{2}+x}{2}-1)\times(\frac{1+2\times\sqrt{2}+x}{2}-2\times\sqrt{2})\times(\frac{1+2\times\sqrt{2}+x}{2}-x)=6\times\sqrt{2}
$$

\LaTeX 的函数：

$$
y=(\frac{1+2\times\sqrt{2}+x}{2})\times(\frac{1+2\times\sqrt{2}+x}{2}-1)\times(\frac{1+2\times\sqrt{2}+x}{2}-2\times\sqrt{2})\times(\frac{1+2\times\sqrt{2}+x}{2}-x)-6\times\sqrt{2}
$$
16

说一句：就不能变成海伦公式吗

17

先证偶函数，这样就只用考虑x>=0

18

这个就是海伦公式来的

19

那求三角形剩下那边长不用这么麻烦

20

用公式求sin(看行不行），行就推出cos用余弦