2. 线段树2
题目ID:7337必做题100分
最新提交:
Wrong Answer
0 分
历史最高:
Wrong Answer
0 分
时间限制: 1000ms
空间限制: 524288kB
题目描述
如题,已知一个数列,你需要进行下面三种操作:
- 将某区间每一个数乘上 x
- 将某区间每一个数加上 x
- 求出某区间每一个数的和
输入格式:
第一行包含三个整数 n,m,p,分别表示该数列数字的个数、操作的总个数和模数。
第二行包含 n 个用空格分隔的整数,其中第 i 个数字表示数列第 i 项的初始值。
接下来 m 行每行包含若干个整数,表示一个操作,具体如下:
操作 1: 格式:1 x y k 含义:将区间 [x,y] 内每个数乘上 k
操作 2: 格式:2 x y k 含义:将区间 [x,y] 内每个数加上 k
操作 3: 格式:3 x y 含义:输出区间 [x,y] 内每个数的和对 p 取模所得的结果
样例:
输入:
5 5 38 1 5 4 2 3 2 1 4 1 3 2 5 1 2 4 2 2 3 5 5 3 1 4
输出:
17 2
数据规模:
对于 30% 的数据:n≤103,m≤104
对于 100% 的数据:n≤105,m≤105,p=571373 k≤1e18。
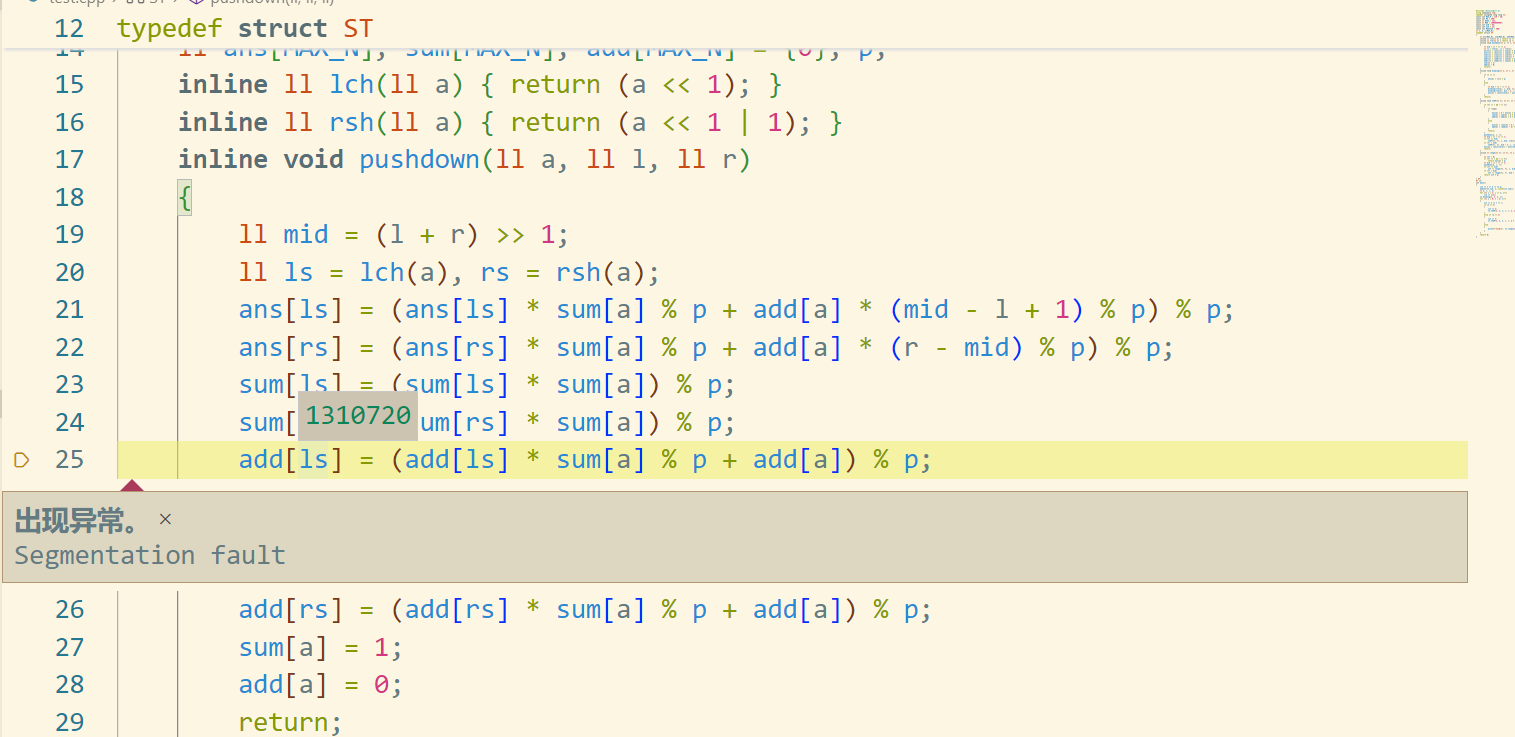
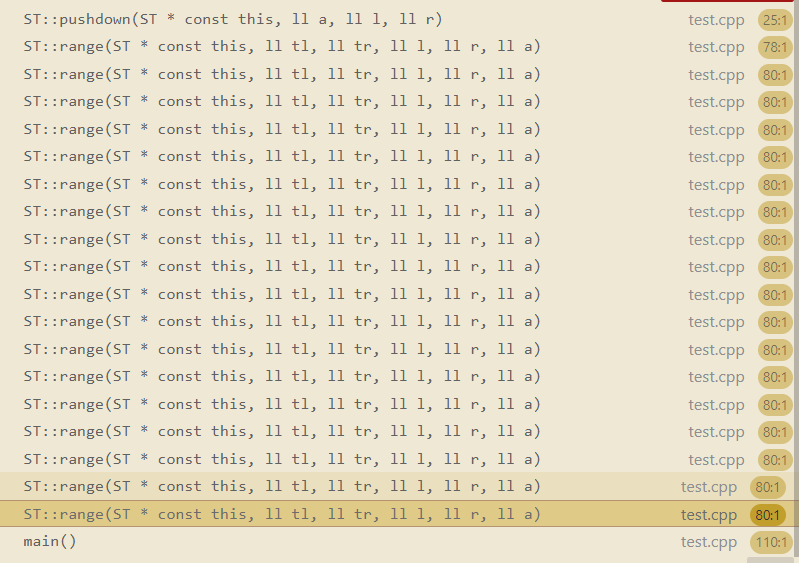
RE:
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ll;
const int MAX_N=1e6+10;
const int MX=100;
const ll BASE=131;
const ll MOD=10000000007;
const int mxN=84;
const int mxK=14;
const int MAXSIZE=300;
ll n,m,z[MAX_N];
typedef struct ST{
ll ans[MAX_N],sum[MAX_N],add[MAX_N]={0},p;
inline ll lch(ll a){return (a<<1);}
inline ll rsh(ll a){return (a<<1|1);}
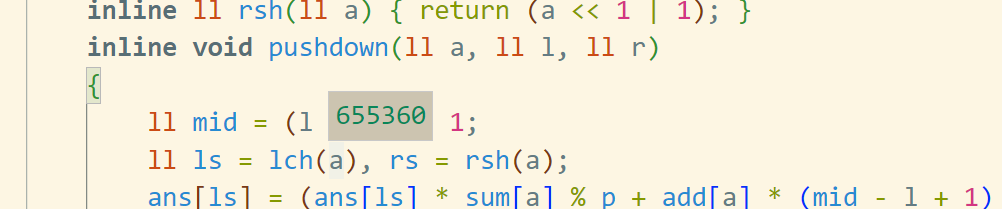
inline void pushdown(ll a,ll l,ll r){
ll mid=(l+r)>>1;
ll ls=lch(a),rs=rsh(a);
ans[ls]=(ans[ls]*sum[a]%p+add[a]*(mid-l+1)%p)%p;
ans[rs]=(ans[rs]*sum[a]%p+add[a]*(r-mid)%p)%p;
sum[ls]=(sum[ls]*sum[a])%p;
sum[rs]=(sum[rs]*sum[a])%p;
add[ls]=(add[ls]*sum[a]%p+add[a])%p;
add[rs]=(add[rs]*sum[a]%p+add[a])%p;
sum[a]=1;
add[a]=0;
return;
}
inline void building(ll a,ll l,ll r,ll *v){
if(l==r){ans[a]=v[l]%p;}
else{
ll mid=(l+r)>>1;
biuding(lch(a),l,mid,v);
biuding(rsh(a),mid+1,r,v);
ans[a]=(ans[lch(a)]+ans[rsh(a)])%p;
}
return;
}
inline void toUP(ll tl,ll tr,ll l,ll r,ll a,ll b,bool type){
if(tl<=l&&r<=tr){
if(type){
ans[a]=b*ans[a]%p;
sum[a]=sum[a]*b%p;
add[a]=add[a]*b%p;
}else{
ans[a]=(ans[a]+b*(r-l+1))%p;
add[a]=(add[a]+b)%p;
}
return;
}
pushdown(a,l,r);
ll mid=(l+r)>>1;
if(tl<=mid)toUP(tl,tr,l,mid,lch(a),b,type);
if(tr>mid)toUP(tl,tr,mid+1,r,rsh(a),b,type);
ans[a]=(ans[lch(a)]+ans[rsh(a)])%p;
return;
}
inline ll range(ll tl,ll tr,ll l,ll r,ll a){
ll cnt=0;
if(tl<=l&&r<=tr)return ans[a]%p;
ll mid=(l+r)>>1;
pushdown(a,l,r);
if(tl<=mid)cnt+=range(tl,tr,l,mid,lch(a))%p;
if(tr>mid)cnt+=range(tl,tr,mid+1,r,rsh(a))%p;
return cnt%p;
}
}ST;
ST st;
int main(){
cin>>n>>m>>st.p;
memset(st.sum,1,sizeof(st.sum));
ll a,l,r,k;
for(ll i=1;i<=n;i++)cin>>z[i];
st.building(1,1,n,z);
for(ll i=0;i<m;i++){
cin>>a>>l>>r;
if(a==1){
cin>>k;
st.toUP(1,1,n,l,r,k,1);
}else if(a==2){
cin>>k;
st.toUP(1,1,n,l,r,k%st.p,0);
}else{
printf("%lld\n",st.range(1,1,n,l,r)%st.p);
}
}
return 0;
}