林老师正在尝试发明一种新的二维魔方。现在给你一个n×n的二维魔方,例如一个3×3的魔方形如下图
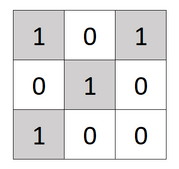
众所周知魔方都可以进行旋转,所以也支持你对这个二维魔方做旋转,我们定义它可以进行下面的四种旋转任意次
- 将所有的行循环上移,行号为1的上移一行后行号为n,其余行号都视为减1
- 将所有的行循环下移,行号为n的下移一行后行号为1,其余行号都视为加1
- 将所有的列循环左移,列号为1的左移一行后列号为n,其余列号都视为减1
- 将所有的列循环右移,列号为n的右移一行后列号为1,其余列号都视为加1
例如将刚才的矩阵,应用一次操作3后,将形如下图
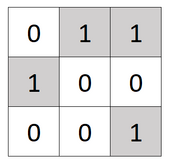
又众所周知,魔方又存在一个还原状态,所以我们定义我们的二维魔方的还原状态为变成了一个左对角线上都为1,其余部分都为0的矩阵,形如下图
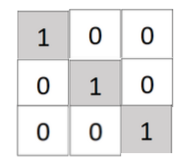
又又众所周知,可能存在上面四种操作,无法还原魔方的情况,所以我们再加入一种操作
翻转:即将某个位置从1变成0,0变成1
但是要注意,每翻转一次这个魔方,都需要消耗1个单位的电力,但是旋转不需要消耗电力。翻转操作只能在执行完所有的旋转操作以后进行
又又又众所周知,林老师只会发明,不会求解,所以现在给定你一个魔方,求魔方变成还原状态所消耗的最少电量
输入格式(Format Input)
每组数据先输入一个整数 n(1≤n≤2000)。 接下来是一个n*n的矩阵,且仅由 0 和 1 组成。 保证所有测试用例中 n² 的值之和不超过 4×10⁶ 。
输出格式(Format Output)
每组数据输出一个整数,即变成 还原状态的最少电量
样例(Sample)
输入样例1 (Sample Input 1) 复制
5 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0
输出样例1 (Sample Output 1)
0
限制(Restrictions)
*时间限制:*1000 ms
*内存限制:*105536 KB
说明/提示(Hint)
在测试用例中,你可以通过对魔方执行操作 2(即把行向上循环移动两次)来得到一个还原状态 。
WA代码:
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
cin >> n;
vector<vector<int>> ma(n, vector<int>(n));
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
cin >> ma[i][j];
}
}
vector<int> d_C(n, 0);
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
if (ma[i][j] == 1)
{
int delta = (j - i + n) % n;
d_C[delta]++;
}
}
}
int ans = 0;
for (int data = 0; data < n; data++)
{
if (d_C[data] > ans)
{
ans = d_C[data];
}
}
cout << n - ans << "\n";
return 0;
}