\Huge{先赞后看,养成习惯}
\huge{中国剩余定理}
模板题
模板题*2
其中, 这题是我的第一道紫题
先看例题:
"现在有个数不知道是多少,只知道其除以3之后余2,除以5之后余3,除以7之后余2,问这个数最小是多少?"
开始讲求解此问题的步骤
步骤1:分解
将这个问题分解成三个子问题:
1、"其除三后余一,除五后余零,除七后余零"
2、"其除三后余零,除五后余一,除七后余零"
3、"其除三后余零,除五后余零,除七后余一"
步骤2:解答子问题
鹅鹅鹅鹅鹅…暴力就行了,比如第一个,每次+lcm(5,7),看看%3是否为0,求出答案为:
70,以此类推,另外两个求出答案为21,15
在这介绍另一种方法:
已知x为5和7的公倍数,所以设x=35y,其中35为lcm(5,7);所以35y≡1(mod 3)
35y%3=2y,式子变换为y≡ \frac{1}{2} (mod 3),很明显,我们还要求y的逆元,1* 2^{3-2} =2,求出x=35*2=70,以此类推,另外两个为21,15
步骤3:合并
要和原问题中结合,求出算式为:
"2*70+3*21+2*15=233"
其中第一个2表示(x%3==2),第二个3表示(x%5==3),第三个2表示(x%5==3)。
步骤4:取余
要将233取模lcm(3,5,7)也就是105,得出答案等于23
证明过程
一、首先我们要明确中国剩余定理是针对两两互素的模数进行求解的。假设我们有n个个不同的互素模数:m[1],m[2],…,m[n]。令M=m[1] * m[2] * … * m[n],且Mi=M/mi,其中1≤i≤n。
二、定理的主要思想是通过构造一个等差数列,使得该等差数列模除每个模数mi的余数相等。设x是满足条件的数,那么我们有以下等式:
x≡a[1](mod m[1]){x%m[1]=a[1]}
x≡a[2](mod m[2]){x%m[2]=a[2]}
...
x≡a[n](mod m[n]){x%m[n]=a[n]}
三、我们将上述等式转化为如下的等差数列形式:
x≡a[1]+k[1]*m[1](mod m[1]*m[2]*...*m[n]){x%lcm(m[1],m[2].....m[n]=m[1]*未知数+余数}
x≡a[2]+k[2]*m[2](mod m[1]*m[2]* ... *m[n]){x%lcm(m[1],m[2].....m[n]=m[2]*未知数+余数}
...
x≡a[n]+k[n]*m[n](mod m[1]*m[2]* ... *m[n]){x%lcm(m[1],m[2].....m[n]=m[n]*未知数+余数}
k[i]为一个整数
四、根据模运算的性质,可以将上述等式简化如下:
x≡∑(ai*Mi*Mi')(mod m)
其中Mi'是Mi的逆元,满足Mi*Mi'≡1(mod mi)。
根据欧几里得算法,可以计算M的逆元Mi',即可得到x的取值
综上所述,中国剩余定理通过将复杂的模线性方程组转化为若干个简单的模线性方程,从而简化了求解过程,并提高了解题效率。其核心思想是通过构造一个等差数列,使得该数列模除每个模数的余数相等,然后根据模运算的性质进行计算求解
接下来开始深入中国剩余定理:
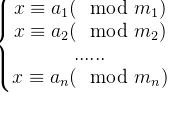
这,是一组同余方程,它共n个,且m[i]到m[n]两两互质用上文方法,一个一个开始“孤立”。
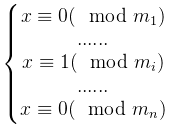
这样整个方程组只剩一个同余于1,其他为0,我们设n为所有 的乘积,还记得y吗?我们分解成许多y[i],现在我们通过式子将y[i]的值写出来,
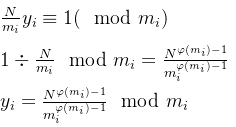
注:请谨慎辨别下方算式,(举个栗子)当a在模p意义下且a与p不互质时,a没有逆元!
有了y[i],便可求得
![]()
好,问题又来了,为啥没有lcm?因为前面说过两两互质
~。~ 终于写完了
伪代码:
void crt(long long &a1,long long &aa){
if(a1<b) /*交换aa和b,交换a1和a(小优化)*/;
long long l=/*aa和b1的最小公倍数(小优化too)*/;
while(/*a1/b后不等于a*/&&/*a1小于等于l*/)a1+=aa;
if(a1>l) a1=0,aa=1;
else aa=l;
}
int main(){
//输入n
for(int i=1~n){
//输入a和b
a%=b;
crt(sum,ans);
}
//输出sum
}
(本代码是暴力+优化,巨佬可以求逆元,而我这种蒟蒻只能暴力出奇迹…)
总结
中国文化博大精深,更适合中国宝宝体质。