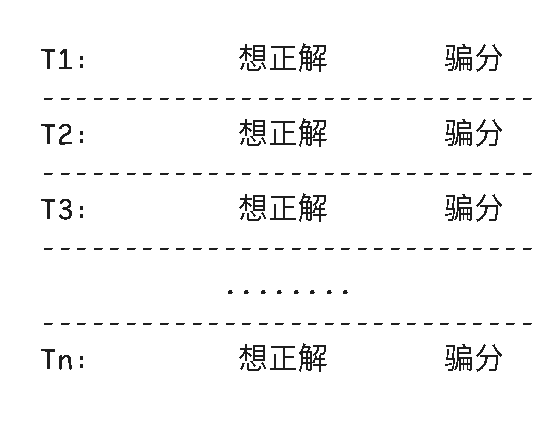
既然是分组背包，那么一定要分组。
我们可以考虑这样分：
这样，就分成了 n 组，每组有 2 个物品。
这是分组背包的核心代码：
for(int i=1;i<=t;i++)for(int j=v;j>=0;j--)for(int k=0;k<(int)w[i].size();k++)if(j>=w[i][k])dp[j]=max(dp[j],dp[j-w[i][k]]+v[i][k]);
可以发现，其中(int)w[i].size()就是每一组物品的个数，但我们已经明确了每一组的物品个数为 2 ，就可以简化一下：
for(int i=1;i<=t;i++)for(int j=v;j>=0;j--)for(int k=0;k<2;k++)if(j>=w[i][k])dp[j]=max(dp[j],dp[j-w[i][k]]+v[i][k]);
如果再把for(int k=0;k<2;k++)转换一下（因为并没有用vector存分数和时间）,就可以展开成这样：
if(j>=t1[i])dp[j]=max(dp[j],dp[j-t1[i]]+w1[i]);
if(j>=t2[i])dp[j]=max(dp[j],dp[j-t2[i]]+w2[i]);
最终就变成了这样：
for(int i=1;i<=n;i++)
for(int j=t;j>=0;j--){
if(j>=t1[i])dp[j]=max(dp[j],dp[j-t1[i]]+w1[i]);
if(j>=t2[i])dp[j]=max(dp[j],dp[j-t2[i]]+w2[i]);
}
给想抄题解的人一句话
