关于线段树（更新中QaQ，管理别关啊）

俞天行 · 2025 年1 月 31 日 12:20

0. 前言 && 目录

此篇献给我最爱的线段树。——世界著名棕名 ytx.

1. 引入
 2. 基本操作
 3. 懒惰标记
（以下内容制作中qwq）
4. 动态开点线段树
5. 线段树合并
6. 线段树分裂
7. 线段树优化建图
8. 拓展 - 李超线段树
9. 拓展 - 猫树

1. 引入

1.1 问题

有这样一个问题

大致题面

已知一个数列，你需要进行下面两种操作：

将某区间每一个数加上 k 。
求出某区间每一个数的和。

乍一看，这是一道水题，但我们一看友好数据范围会毛骨悚然：

对于 30\% 的数据： n \le 8 ， m \le 10 。
对于 70\% 的数据： n \le {10}^3 ， m \le {10}^4 。
对于 100\% 的数据： 1 \le n, m \le {10}^5 。
保证任意时刻数列中所有元素的绝对值之和 \le {10}^{18} 。

{10}^5 ！这个数字虽然不是很大，但是根据题目要求，我们需要反复遍历某一区间，很显然，正常的暴力写法显然会超时。~~那我们该何去何从呢？~~

1.2 方法

Q：有没有办法来维护区间信息并且不会超时呢？
A：线段树！！！

1.2.1 简介

线段树（Segment tree）是常用来维护 区间信息 的数据结构。

它是一棵不那么完全的二叉树

维护序列的区间信息
所有非叶节点都有两个儿子
树上每个节点对应序列的一个区间

它可以在 O(\log N) 的时间复杂度内实现单点修改、区间修改、区间查询（区间求和，求区间最大值，求区间最小值）等操作。

1.2.2 基本结构

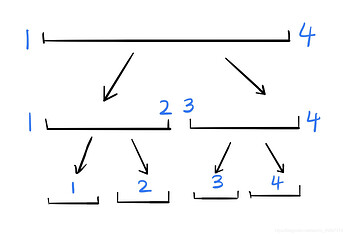
线段树是一种二叉树，也就是对于一个线段，我们会用一个二叉树来表示。如下图，一个长度为4的线段，我们可以表示成这样：

简略可以表示成：

	       [1, 4]
		   /    \
	   [1, 2]   [3, 4]
	    /  \     /   \
   [1, 1][2, 2][3, 3][4, 4]

为什么这么表示呢？如果你要表示线段的和，那么最上面的根节点的权值表示的是这个线段 1\sim 4 的和。根的两个儿子分别表示这个线段中 1\sim 2 的和，与 3\sim 4 的和。以此类推。

1.2.3 时间复杂度

线段树的时间复杂度主要取决于其操作类型和树的深度。以下是常见操作的时间复杂度分析：

1.2.3.1. 构建线段树

时间复杂度： O(N)
- 在构建线段树时，我们需要为每个区间节点分配空间，并且从底部逐层构建树。总的构建过程是线性时间复杂度，即 O(N) ，其中 N 是数组的大小。

1.2.3.2. 区间查询

时间复杂度： O(\log N)
- 线段树是一个高度平衡的二叉树，树的高度为 O(\log N) 。查询时，我们最多需要沿树的高度遍历，检查与查询区间重叠的节点。由于线段树可以将查询操作分解为多个子区间查询，因此每次查询操作的时间复杂度是 O(\log N) 。

1.2.3.3. 单点更新

时间复杂度： O(\log N)
- 单点更新是通过从叶节点更新到根节点的方式进行的。由于线段树的高度为 O(\log N) ，更新操作最多需要经过 O(\log N) 个节点，所以时间复杂度为 O(\log N) 。

1.2.3.4. 区间更新

时间复杂度： O(\log N) （如果使用懒惰标记）
- 区间更新是更新一个区间的所有元素。在线段树中，使用懒惰标记优化区间更新操作，可以将区间更新的时间复杂度降低到 O(\log N) ，而不是 O(N) ，其中 O(\log N) 是树的高度。如果没有懒惰标记，可能需要更新整颗树的多个节点，复杂度为 O(N) 。

2. 基本操作

2.1 建树

明白了线段树长什么样，我们就能建树了！
我们用一个结构体来表示一个线段树内的信息：

struct node {
	int l; //左儿子的下标
    int r; //右儿子的下标
	int sum; //当前区间元素之和
} tree[/*这里开多大？*/];

对呀，这里到底开多大？我们知道如果是完全二叉树要开 2n 就行了，那线段树也是这样吗？

Yes
No

0 投票人

揭晓答案：No！！！
Why?
是这样的，线段树是个类似完全二叉树的结构，但是开空间时要为下面一层留足空间，考虑从上至下估计每层节点之和，得到

1+2+4+⋯+2^{⌈logn⌉}≤2^{⌈logn⌉+1}

所以，一般开到 4n 即可。

那么到底怎么建树呢？
考虑以下问题：

当前节点 i 的权值等价于什么？

\because 1\sim 4 的和就是等于 1\sim 2 的和与 2\sim 3 的和的和。
\therefore 节点 i 的权值 = 她的左儿子权值 + 她的右儿子权值。

我们知道，一颗从 1 开始编号的二叉树，结点 i 的左儿子和右儿子编号分别是 2\times i 和 2\times i + 1 。

那么我们可以得到式子：

tree[num].sum = tree[num << 1].sum + tree[num << 1 | 1].sum;

那么我们就能建树了（因为需要上式操作的时候很多，所以我们把它单独写进 pushup 这个函数里）！

建树代码

void build(int num, int l, int r) {
	/*
	1.确定左右端点
	2.判断是否为叶子
	3.构建左右子树
	*/
	tree[num].l = l;
	tree[num].r = r;
	
	if (l == r) {
		tree[num].sum = a[l];
		return ;
	}
	
	int mid = (l + r) >> 1;
	
	build(num << 1, l, mid); //构造左子树
	build(num << 1 | 1, mid + 1, r); //构造右子树
	
	pushup(num); //刚才我们发现的性质return
	
	return ;
}

2.2 区间求和

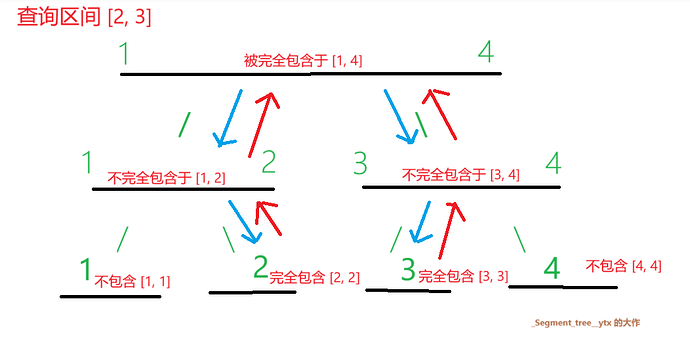
这是一棵长度为 4 的线段树

	       [1, 4]
		   /    \
	   [1, 2]   [3, 4]
	    /  \     /   \
   [1, 1][2, 2][3, 3][4, 4]

我们考虑如下情况，需要查找 [1, 2] 的值，我们只需要顺着 [1, 4] 的左子树往下走，就能得到区间 [1, 2] 的权值，可如果要查询 [2, 3] 呢？

那么我们就能写出代码了！

完全包含
不完全包含
不包含

区间求和代码

int query(int num, int L, int R) {
	//考虑num的区间不在L-R之内
	if (tree[num].r < L || tree[num].l > R) return 0;
	
	//完全包含
	if (tree[num].l >= L && tree[num].r <= R) {
		return tree[num].sum;
	}
	
	return query(num << 1, L, R) + query(num << 1 | 1, L, R);
}

这样，我们就能AK A+B Problem了！

完整A+B Problem代码

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 5;

int a[N];

struct node {
	int l, r;
	int sum;
} tree[N << 2];

void build(int num, int l, int r);
void pushup(int num);
int query(int num, int L, int R);

int main(void) 
{
	int n = 2;
//	cin >> n;
	
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	
	build(1, 1, n);
	
	int l = 1, r = 2;
//	cin >> l >> r;
	
	cout << query(1, l, r);

	return 0;
}

void build(int num, int l, int r) {
	/*
	1.确定左右端点
	2.判断是否为叶子
	3.构建左右子树
	*/
	tree[num].l = l;
	tree[num].r = r;
	
	if (l == r) {
		tree[num].sum = a[l];
		return ;
	}
	
	int mid = (l + r) >> 1;
	
	build(num << 1, l, mid);
	build(num << 1 | 1, mid + 1, r);
	
	pushup(num);
	
	return ;
}

void pushup(int num) {
	tree[num].sum = tree[num << 1].sum + tree[num << 1 | 1].sum;
}

int query(int num, int L, int R) {
	//考虑num的区间不在L-R之内
	if (tree[num].r < L || tree[num].l > R) return 0;
	
	//完全包含
	if (tree[num].l >= L && tree[num].r <= R) {
		return tree[num].sum;
	}
	
	return query(num << 1, L, R) + query(num << 1 | 1, L, R);
}

3. 懒惰标记

3.0 引入

传统的线段树（没有懒惰标记）对于区间更新操作，通常需要递归地更新每一个节点，并且每个节点都需要维护当前区间的状态（例如区间和、区间的最小值等）。假设我们要将某一区间 [L, R] 的值加上某个常数 x ，在线段树中，对于每个节点，都必须遍历并更新相关的区间。这就会导致时间复杂度较高！

~~那我们该何去何从呢？~~

3.1 懒惰标记的定义

懒惰标记（lazy tag） 是一种常用于线段树中优化区间更新操作的技术。它的核心思想是 延迟更新，即不立即对每个节点进行更新，而是将更新操作推迟到真正需要的时候进行，减少不必要的计算，优化性能。

3.2 懒惰标记的工作原理

懒惰标记的基本思路是：在更新某个区间时，标记该区间需要更新，而不是立刻进行更新 。只有当查询某个区间时，才会实际应用那些标记的更新，并将更新传递给子节点。通过这种方式，避免了不必要的重复更新，极大提高了效率。

在传统的线段树中，区间更新操作（例如将一个区间内的每个元素加上一个常数）通常需要递归地更新树中的每个节点，这样的操作可能导致较高的时间复杂度（特别是当区间较大时）。懒惰标记的出现就是为了减少这些重复的更新操作。

3.3 懒惰标记的用法

我们需要在表示线段树的结构体里再添一项表示懒标记，来记录这个区间：

int tag;

那么区间修改的时候，我们按照如下原则：

如果当前区间被完全覆盖在目标区间里，讲这个区间的 sum+k*(tree[i].r-tree[i].l+1)
如果没有完全覆盖，则先下传懒标记
如果这个区间的左儿子和目标区间有交集，那么搜索左儿子
如果这个区间的右儿子和目标区间有交集，那么搜索右儿子

3.3.1 pushup & pushdown

标记下放线段树要实现两个功能：
pushdown → 将当前节点暂存的标记信息传递给子节点
pushup → 用子树的信息更新当前节点

每次要进入子树时 pushdown ，从子树更新信息返回时 pushup 。

pushdown & pushup代码

void pushdown(int num) {
	tree[2 * num].sum += (tree[2 * num].r - tree[2 * num].l + 1) * tree[num].tag;//更新左子树区间和
	tree[2 * num].tag += tree[num].tag;//累加tag
	tree[2 * num + 1].sum += (tree[2 * num + 1].r - tree[2 * num + 1].l + 1) * tree[num].tag;//更新右子树区间和
	tree[2 * num + 1].tag += tree[num].tag;//累加tag
	tree[num].tag = 0;//清零
	return;
}

void pushup(int num) {
	tree[num].sum = tree[2 * num].sum + tree[2 * num + 1].sum;//用子树的和更新当前节点的和
	return;
}

3.3.2 区间加 & 区间求和

区间加 & 区间求和代码实现如下：

void modify(int num, int L, int R, int x) {
	if (tree[num].r < L || R < tree[num].l) return; //当前区间与修改区间不相交，直接返回
	
	//当前区间正好被修改区间包含，直接修改
	if (L <= tree[num].l && tree[num].r <= R) {
		tree[num].sum += (tree[num].r - tree[num].l + 1) * x;
		tree[num].tag += x;
		return;
	}

	if (tree[num].tag != 0) pushdown(num); //下放标记
	modify(2 * num, L, R, x); //递归左子树
	modify(2 * num + 1, L, R, x); //递归右子树
	pushup(num); //更新当前区间和
	return;
}

int query(int num, int L, int R) {
	if (tree[num].r < L || R < tree[num].l) return 0; //考虑num的区间不在L-R之内
	if (L <= tree[num].l && tree[num].r <= R)return tree[num].sum; //当前区间正好被查询区间包含，直接返回区间和

	if (tree[num].tag != 0)pushdown(num);
	return query(2 * num, L, R) + query(2 * num + 1, L, R); //左子树中的部分区间与右子树中的部分之和
}

4. 动态开点线段树

4.1 概念

前面讲到需要给线段树开 4n 大小的数组。为了节省空间，我们可以不一次性建好树，而是在最初只建立一个根结点代表整个区间。当我们需要访问某个子区间时，才建立代表这个区间的子结点。这样我们不再使用 2i 和 2i+1 代表 i 结点的儿子，而是用 l 和 r 记录儿子的编号。

总之，动态开点线段树的核心思想就是：结点只有在有需要的时候才被创建 。

单次操作的时间复杂度是不变的，为 O(\log N) 。由于每次操作都有可能创建并访问全新的一系列结点，因此 m 次单点操作后结点的数量规模是 O(m \log N) 。最多也只需要 2n-1 个结点，没有一点浪费，~~对于强迫症患者十分友好~~。

4.2 基本操作

单点修改：

// root 表示整棵线段树的根结点；cnt 表示当前结点个数
int n, cnt, root;
int sum[n * 2], l[n * 2], r[n * 2];

// 用法：modify(root, 1, n, x, f); 其中 x 为待修改节点的编号
void modify(int& num, int s, int t, int x, int f) {  // 引用传参
	if (!num) num = ++cnt;  // 当结点为空时，创建一个新的结点
	if (s == t) {
		sum[num] += f;
		return;
	}
	int m = s + ((t - s) >> 1);
	if (x <= m)
		modify(l[num], s, m, x, f);
	else
		modify(r[num], m + 1, t, x, f);
	sum[num] = sum[l[num]] + sum[r[num]];  // pushunum
}

区间询问：

// 用法：query(root, 1, n, L, R);
int query(int num, int s, int t, int L, int R) {
	if (!num) return 0;  // 如果结点为空，返回 0
	if (s >= L && t <= R) return sum[num];
	int m = s + ((t - s) >> 1), ans = 0;
	if (L <= m) ans += query(l[num], s, m, L, R);
	if (R > m) ans += query(r[num], m + 1, t, L, R);
	return ans;
}

5. 线段树合并

俞天行 · 2025 年1 月 31 日 12:22

这篇文章会讲很多关于线段树的东西（线段树合并、线段树分裂、线段树优化建图都会讲），会定时更新的，有没有想要我讲的QaQ。看到了就点个赞吧。。。

稻叶昙 · 2025 年1 月 31 日 12:31

主播主播你的线段树确实很强，但是太吃脑细胞了，有没有更加简单的代码实现呢？

有的兄弟，有的，这题的解法还有5个

~~指令集，平衡树，CDQ分治，分块，树状数组~~

俞天行 · 2025 年1 月 31 日 12:32

666

2345安全卫士 · 2025 年1 月 31 日 12:34

主播主播你的这几个算法确实很强，但还是太吃操作了，有没有更加简单的算法呢？

有的兄弟，有的，这样的算法还有9个：

题解、老师、同学、AC代码、复制、~~wyd~~、奖励、Crtl、还有一个暴力

俞天行 · 2025 年2 月 2 日 00:40

又更新了QaQ