感谢 @金裕仓 对此题解的贡献。
题面
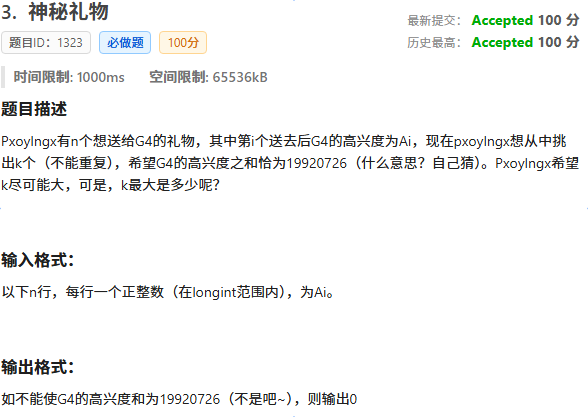
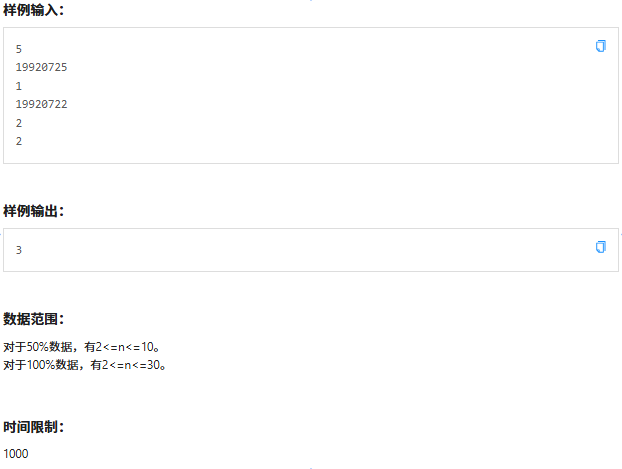
本题数据范围很小,考虑搜索。
对于每一个数,我们可以选或不选(经典的0-1问题),时间复杂度 O(2^n)
我们把DFS设置3个参数 (x,k,s) , x 表示当前位置, k 表示已经选了多少个, s 表示已选数的和。如果 x>n ,
DFS代码如下:
void dfs(int x,int k,int s){
if(x>n){//边界
return;
}
if(s==19920726){
ans=max(ans,k);
/*
注意:这里不能返回,因为可能会有0的情况,导致答案错误。
by 金裕仓
*/
}
dfs(x+1,k,s);//不选
dfs(x+1,k+1,s+a[i]);//选
}
但是,极限数据会让这份代码TLE (2^{30}=1,073,741,824) ,所以让我们迎来重头戏——剪枝
本题需要的剪枝技巧有:①可行性剪枝 ②优化搜索顺序
我们一个一个看。
可行性剪枝
Part 1
如果某一时刻 s 超过了 19920726 ,就停止搜索。
因为如果 s>19920726 ,以后不管怎么选都不可能等于 19920726 。
Part 2
前缀和优化(感谢 @金裕仓)
如果某一时刻 s 加上以后的所有数还小于 19920726 ,就停止搜索。
因为就算以后的全选都不可能等于 19920726 。
优化搜索顺序
(感谢 @金裕仓)
把数组排好序(从大到小),可以减少时间复杂度
代码就不放了,感谢阅读。