点赞破5,讲个好证明的高斯消元。
一道算法总得有模版题。
不会打 LATEX 直接贴张图片。
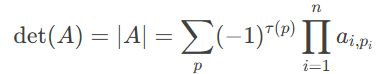
我们先不管这个题。
思考这么一个问题。
给定 n 个 n 维向量,求它构造出的 n 维物体的体积是多少。
我们看它满足什么性质。
1. 将一条边延长 k 倍,体积乘 k 。
2. 交换两个向量体积取反。
然后根据一大堆式子(我是蒟蒻不会推,会推了,会再发一篇)
得到体积就是行列式的值
然后可以根据这性质弄到一个倒三角矩阵。
最终答案就是对角线和。
我们再准备一个变量,每交换两行,就 +1 ,最终如果是奇数 ans=-ans
给出行列式怎么求,求值写得很明白值自己思考。
for(int i=1;i<=n;++i)
{
for(int j=i+1;j<=n;++j)
{
while(a[i][i])
{
int val=a[j][i]/a[i][i];
for(int k=i;k<=n;++k) a[j][k]-=val*a[i][k],a[j][k]%=Mod;
cnt++;
swap(a[i],a[j]);
}
cnt++;
swap(a[i],a[j]);
}
}