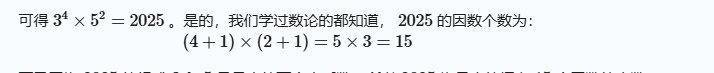据野史记载, 2025 是一个年份(美丽的废话)。
我们都知道, 2025=45 \times 45=45^2
当然, 2025 也可以分解成 3^4 \times 5^2 ,分解过程如下(当然,这是一个可以口算出来的东西,不过我们可以利用上述结论来推算出来):
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,45^2=2025
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(5 \times 9)^2=2025
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,5^2 \times 9^2=2025
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,9^2 \times 5^2=2025
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(3^2)^2 \times 5^2=2025
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3^{2 \times 2} \times 5^2=2025
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3^4 \times 5^2=2025
可得 3^4 \times 5^2=2025 。是的,我们学过数论的都知道, 2025 的因数个数为:
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(4+1) \times (2+1)=5 \times 3=15
而又因为 2025 的组成 3 和 5 是最小的两个奇质数,所以 2025 为最小的拥有 15 个因数的奇数。
拓展:有 15 个因数的最小数为 144 ,可以分解为 2^4 \times 3^2 。 144 的因数分别是 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,1、2、3、4、6、8、9、12、16、18、24、36、48、72、144。
接下来,我们的目光来到 n^3 上, 2025 虽然好像跟三次方没一点关系,不过他的确为 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,1^3+2^3+3^3+4^3+5^3+6^3+7^3+8^3+9^3
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, 的和。
这就是 2025 的特殊含义,还有什么含义可以下面留言我来补充。