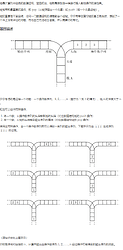
我们先看一道题:
如果暴力枚举,必然超时。
但我们可以通过枚举打一个表,看看能不能发现什么规律:
1 1 2 5 14 42 132恭喜你发现了卡特兰数
什么是卡特兰数
卡特兰数(Catalan number),又称卡塔兰数、明安图数,是组合数学中一种常出现于各种计数问题中的数列。它满足递推式 H_0=H_1=1,H_n=\dfrac{(4n-2)H_{n-1}}{n+1} 。此外,卡特兰数也可以表示为组合数的形式,即 H_i=C_{2n}^n-C_{2n}^{n-1}=\dfrac{C_{2n}^n}{n+1} 。
代码实现:
for(int i=dp[0]=1;i<=n;dp[i]=dp[i-1]*(4*i-2)/(i+1),i++);//递推实现
//组合数容易造成溢出,故不推荐。
卡特兰数的具体应用
如果在luogu上搜索卡特兰数,从橙到黑都有。
其中还包括经典水紫:
这说明,卡特兰数在数学上的应用还是非常广泛的,迄今为止,已发现与卡特兰数相关的数学模型超 50 种。
- 有 2n 个人排成一队顺序购票。入场费 k 元。其中只有 n 个人有一张 k 元纸币,另外 n 人只有 2k 元纸币,剧院无其它纸币,问有多少种方法使得只要有 2k 元的人买票,售票处就有 k 元的钞票找零?
其实稍微思考一下,会发现这个问题和出栈序列本质是一样的,把 k 元想象成入栈, 2k 元想象成出栈就能理解。 - 定义空串为括号匹配序列,若 S 为括号匹配序列,则 (S) 也是括号匹配序列。若 A,B 都为括号匹配序列,则 AB 也为括号匹配序列。求由 n 个左括号和 n 个右括号共能组成多少个括号匹配序列。
这个问题和出栈问题也本质相同,把左括号当成进栈,右括号当成出栈就能理解。 - n 个结点可构造多少个不同的二叉树。
其实可以使用前序遍历,再把前序遍历中的左节点理解成左括号,右节点理解成右括号,就能化为括号匹配问题。 - [TJOI2015]为了提高智商,ZJY 开始学习概率论。有一天,她想到了这样一个问题:对于一棵随机生成的 n 个结点的有根二叉树(所有互相不同构的形态等概率出现),它的叶子节点数的期望是多少呢?
还是使用括号序列理解,先将树转为括号序列,在一个长度为 2(n+1) 的括号序列中,有 n 个位置添加括号(小学一年级奥数植树问题),转化为树后刚好为叶节点。
我们再考虑叶节点的总和,显然为 nH_{n} 。
在套用期望的公式,可以得到期望为 \dfrac{nH_{n}}{H_{n+1}}\\=\dfrac{n(n+1)}{2(2n-1)}
即可AC。