【道路拆除】
题目描述
A 国有 n 座城市,从 1∼n 编号。 1 号城市是 A 国的首都。城市间由 m 条双向道路连通,通过每一条道路所花费的时间均为 1 单位时间。
现在 A 国打算拆除一些不实用的道路以减小维护的开支,但 A 国也需要保证主要线路不受影响。因此 A 国希望道路拆除完毕后,利用剩余未被拆除的道路,从 A 国首都出发,能到达 s_1 号与 s_2 号城市,且所要花费的最短时间分别不超过 t_1 与 t_2 (注意这是两个独立的条件,互相之间没有关联,即不需要先到 s_1 再到 s_2 )。
A 国想请你帮他们算算,在满足上述条件的情况下,他们最多能拆除多少条道路。 若上述条件永远无法满足,则输出 −1 。
输入格式
第一行两个正整数 n,m ,表示城市数与道路数。
接下来 m 行,每行两个正整数 x,y ,表示一条连接 x 号点与 y 号点的道路。数据保证没有重边和自环。
最后一行四个整数,分别为 s_1,t_1,s_2,t_2 。
输出格式
仅一行一个整数,表示答案。
样例 #1
样例输入 #1
5 6
1 2
2 3
1 3
3 4
4 5
3 5
5 3 4 3
样例输出 #1
3
样例 #2
样例输入 #2
3 2
1 2
2 3
2 2 3 1
样例输出 #2
-1
提示
【数据范围】
对于 30\% 的数据, n,m≤15 ;
另有 20\% 的数据, n≤100,m=n−1 ;
另有 30\% 的数据, s_1=s_2 ;
对于 100\% 的数据, 2≤n,m≤3000,1≤x,y≤n,2≤s_1,s_2≤n,0≤t_1,t_2≤n 。
【样例 1 解释】
拆除 (1,2),(2,3),(3,4) 三条边。
注意:不需要令首都与除了 s_1,s_2 外的点在拆除之后依然连通。
【样例 2 解释】
即使一条边都不拆除,首都到 3 号点的最短时间也都达到了 2 单位时间。
对于这道题,我们需要一个通用的图,用来表示所有情况。
那么这个图是什么呢?
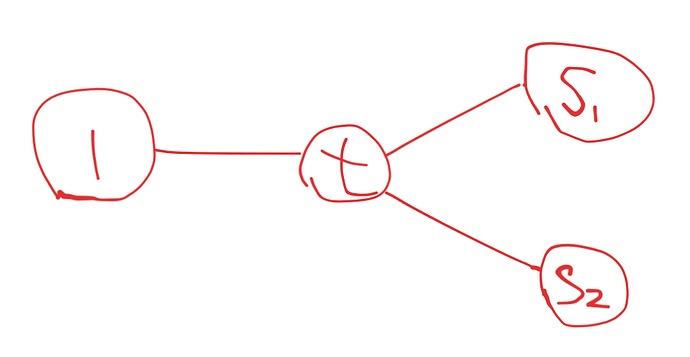
我们知道, A 国首都到达 s_1,s_2 的时候,一定会经过一个共同的点 t ,这样,图不就出来了?
就像这样:
(画的有点丑陋,凑合着看吧)
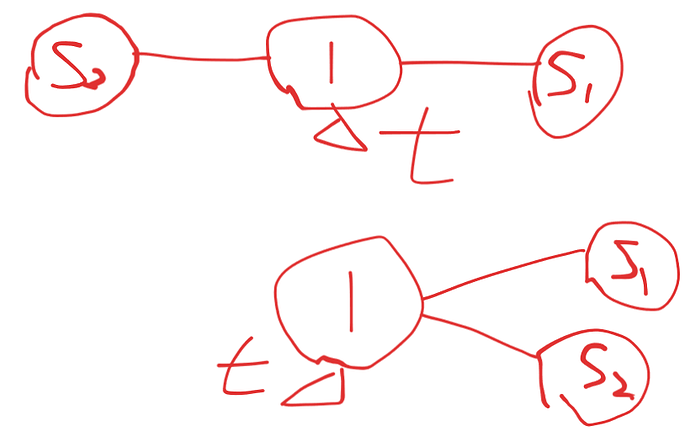
如果是以下的情况,那么 t 就是首都:
现在就好办了,我们只需要使用三次 bfs ,分别为:
bfs(1,0);
bfs(s1,1);
bfs(s2,2);
bfs 后,我们再求出最大值就行了。
for(int i=1~n)
if(dist[i][0]+dist[i][1]<=t1 && dist[i][0]+dist[i][2]<=t2)
ans=max(ans,m-dist[i][0]-dist[i][1]-dist[i][2]);