加油赶工!
道路拆除
题目描述
A 国有 n 座城市,从 1 \sim n 编号。$1$ 号城市是 A 国的首都。城市间由 m 条双向道路连通,通过每一条道路所花费的时间均为 1 单位时间。
现在 A 国打算拆除一些不实用的道路以减小维护的开支,但 A 国也需要保证主要线路不受影响。因此 A 国希望道路拆除完毕后,利用剩余未被拆除的道路,从 A 国首都出发,能到达 s_1 号与 s_2 号城市,且所要花费的最短时间分别不超过 t_1 与 $t_2$(注意这是两个独立的条件,互相之间没有关联,即不需要先到 s_1 再到 $s_2$)。
A 国想请你帮他们算算,在满足上述条件的情况下,他们最多能拆除多少条道路。 若上述条件永远无法满足,则输出 $-1$。
输入格式
第一行两个正整数 $n,m$,表示城市数与道路数。
接下来 m 行,每行两个正整数 $x,y$,表示一条连接 x 号点与 y 号点的道路。
最后一行四个整数,分别为 $s_1,t_1,s_2,t_2$。
输出格式
仅一行一个整数,表示答案。
样例 #1
样例输入 #1
5 6
1 2
2 3
1 3
3 4
4 5
3 5
5 3 4 3
样例输出 #1
3
样例 #2
样例输入 #2
3 2
1 2
2 3
2 2 3 1
样例输出 #2
-1
提示
【数据范围】
对于 30%的数据,n,m <=15;
另有 20\% 的数据,n <= 100$,m <= n-1;
另有 30\% 的数据,s1 = s2;
对于 100\% 的数据,2 <= n,m <= 3000,1<= x,y <= n,2 <= s1,s2 <= n,0 <= t1,t2 <= n。
【样例 1 解释】
拆除 (1,2),(2,3),(3,4) 三条边。
注意:不需要令首都与除了 s_1,s_2 外的点在拆除之后依然连通。
【样例 2解释】
即使一条边都不拆除,首都到 3 号点的最短时间也都达到了 2单位时间。
看完题后,蒟蒻的第一反应是----最短路径,那可太简单了!
刷刷的写完了代码,过了样例。
可定睛一看—好家伙,这题可不能光求最短路径啊!
那么,我们有没有更好的办法呢?
当然有!我们可以设一个节点t,边权为一的最短路径就可以用bfs来解决。
如图:
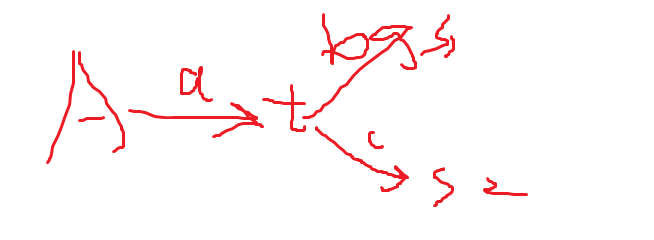
(画的有点丑)
当 a+b<=t1&&a+c<=t2 的时候
答案可以表示为–max{m-(a+b+c))}(对了,别忘了剪枝!)
得到这点后 这题就挺简单了!
(感觉有点没写清楚)
- 1.清楚吧
- 2.清楚
- 3.不清楚
- 不用选(感谢大家的建议,我会继续改进的)