某天,我看见洛谷由新增了几道题目。
啊?GESP的题什么时候这么水了?
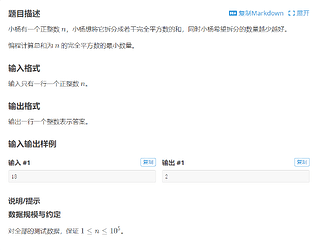
于是,我点开了第一题。
这不就背包模版?
我随手敲了一遍背包:
for(int i=1;i*i<=n;i++){
for(int j=a[i];j<=n;j++){
dp[j]=min(dp[j],dp[j-a[i]]+1);
}
}
轻松 \color{green}{AC} 。
我点开最优解:
看见了某人的“AC”代码,我把它复制下来,准备研究一下。
没想到……
竟然过不了样例
我只好自己想了,于是发了这样一篇帖子。
有位大佬为我细心解答。
于是就有了你看到的这篇帖子。
我先打了个表:
(表太长,略)
似乎没有什么规律,但是我们可以发现:所有的数均不超过 4。
Why?
Because……
四平方和定理 (英语:Lagrange’s four-square theorem) 说明每个正整数均可表示为4个整数的平方和。它是费马多边形数定理和华林问题的特例。——百度百科
所以只需研究在哪些情况下输出分别等于 1,2,3,4 。
于是我又打了四个表:
输出=1
(表太长,略)
不难发现,它们都是完全平方数。
输出=2
(表太长,略)
看起来没有什么规律,先手推一下。
假设 n=a^2+b^2 ,我们在两边同时乘上 c^2 ,可得:
c^2n=(ca)^2+(cb)^2
所以,当 n 拥有平方因子,且能分解成两个平方数之和时,用 n 除去最大的平方因子后,仍能分解成两个平方数之和。(我们将它称为结论 1 )
但我们除去最大的平方因子后,这个数就不再拥有平方因子了。
我们不难发现, (a^2+b^2)(c^2+d^2)\\=a^2c^2+a^2d^2+b^2c^2+b^2d^2\\=(ac)^2+(ad)^2+(bc)^2+(bd)^2\\=((ac)^2+(bd)^2+2abcd)+((ad)^2+(bc)^2-2abcd)\\=(ac+bd)^2+(ad-bc)^2
也就是说,两个二平方和的积依然能分解成二平方和。
所以当某个数的质因数都可以分解为二平方和时,这个数可表示为二平方之和。(我们将它称为结论 2 )
根据结论 2 ,我们可以考虑分解质因数。
例: 99994=2\times 17^2\times 173
根据结论 1 ,去掉所有指数为偶数的,再去掉所有指数。
留下 2 和 173 。
而高斯已经证明,只有模 4 余 3 的质数不能表示为二平方之和。
而 2\,mod\,4=2 ,
173\,mod\,4=1
结果均不为 3 。
所以 99997 能表示为二平方和, 99997=171^2+266^2 。
输出=3
(打表太长,略)
不难证明,形如 8n+7 的数都不能表示为三平方数之和。
证明如下:
假设存在 a,b,c 满足 a^2+b^2+c^2=8n+7
则 a,b,c 必为一奇两偶或三奇。
先讨论一奇两偶的情况:
令 a=2d+1,b=2e,c=2f ,
代入原式得 4d^2+4e^2+4f^2+4d+1=8n+7
等式左边除4余1,右边除4余3,矛盾。
先讨论三奇的情况:
令 a=2d+1,b=2e+1,c=2f+1 ,
代入原式得 4d^2+4e^2+4f^2+4d+4e+4f+3=8n+7
4d^2+4e^2+4f^2+4d+4e+4f=8n+4
d^2+e^2+f^2+d+e+f=2n+1
等式左边为偶数,右边为奇数,矛盾。
而对于形如 4^m(8n+7) 的数也可以用同样的方法证明,大家可以自己推推。
其余情况都可以表示为三平方和。
于是,就有了开头那位大佬的话: