直接贴上链接。
我们可以列一个表。
1/16\\
1/8\,\,1/16\\
1/4\,\,1/8\,\,1/16\\
1/2\,\,1/4\,\,1/8\,\,1/16\\
\,\,\,\,\,\,1\,\,1/2\,\,1/4\,\,1/8\,\,1/16
我们会发现:
- 棋子所在位置的和是不变的。
- 我们如果把这个表中所有数的和都算出来的话。那么我们就会发现,它是个定值。
因为我们先把每列的和算出来,会得到它们,它们分别是:
2\,\,1\,\,1/2\,\,1/4\,\,1/8...
再把它们的和求出来,得到整张表的和为4。
(懒得打dfrac)
然后我们不难发现:
当 n≥4 时,阶梯的和大于 1+\dfrac{1}{2}\times 2+\dfrac{1}{4}\times 3+\dfrac{1}{8}\times 4=\dfrac{13}{4}
空白处的和小于 4-\dfrac{13}{4}=\dfrac{3}{4}
可以发现:
阶梯的和已经大于空白处的和了。
而题中已经给出我们 n=1,2 的解法,而 n≥4 时就可以直接输出 -1 。
所以我们如果用这种方法,最多只会WA这一个点。
在考场实在做不出来的话这样就够了。
接着我们用这种方法敲一遍,竟然AC了。
那为什么 n=3 时无解呢?
手动模拟一遍就知道了。
1.
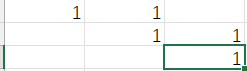
2.
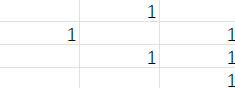
3.
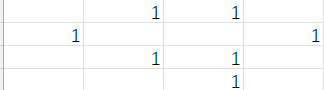
4.
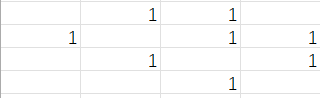
可以发现:
右上方出现了相同的子结构,说明可以无限延伸下去。左下角的三个棋子永远无法挪动。