HH的项链题解
题目描述
HH 有一串由各种漂亮的贝壳组成的项链。HH 相信不同的贝壳会带来好运,所以每次散步完后,他都会随意取出一段贝壳,思考它们所表达的含义。HH 不断地收集新的贝壳,因此,他的项链变得越来越长。
有一天,他突然提出了一个问题:某一段贝壳中,包含了多少种不同的贝壳?这个问题很难回答…… 因为项链实在是太长了。于是,他只好求助睿智的你,来解决这个问题。
【数据范围】
对于 20\% 的数据, 1\le n,m\leq 5000 ;
对于 40\% 的数据, 1\le n,m\leq 10^5 ;
对于 60\% 的数据, 1\le n,m\leq 5\times 10^5 ;
对于 100\% 的数据, 1\le n,m,a_i \leq 10^6 , 1\le l \le r \le n 。
本题可能需要较快的读入方式,最大数据点读入数据约 20MB
思路分析
莫队
这一题题意还是很清晰的,给定一组数,求一段区间里有多少不同的数字。
当然解法很多,可以用离线+树状数组,莫队来做,我们先说一下莫队的思路:
我们定义 cnt[i] 为数字 i 在一段区间里存在的个数,我们定义一个双指针 L,R , R 指针每扫过一个便使 cnt[a[i]]++ ,如果此时 cnt==1 ,说明这个数是第一次出现的, ans++ ,这样就能得到 [1,r] 区间每个数字出现的个数了 ,这时我们再让 L 从头开始扫,每扫到一个数便使 cnt[a[i]]-- ,如果此时 cnt==0 说明此时我们扫过的区间这个数已经不存在了, ans-- ,这样我们就能得到 [l,r] 这出现了多少数字。
这是一种暴力而且好想的思路,时间复杂度是 O(nm) ,显然过不去的,于是我们便要对这个算法进行改进。
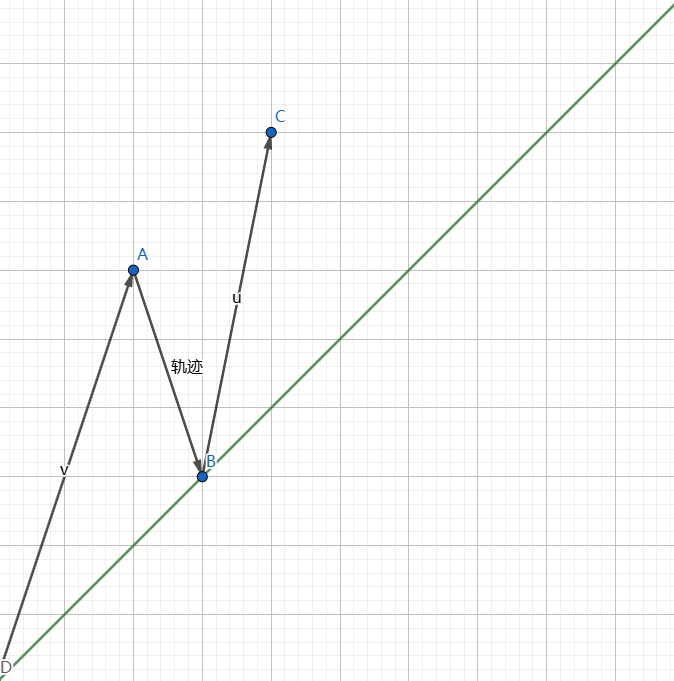
我们不妨把一个区间 [l,r] 看成平面上的一个点 (x,y) ,此时我们暴力法的移动,便可以看成平面上坐标点的移动了,计算量就是两点之间的曼哈顿距离, m 次查询,相当与从原点出发,用一条直线连接这 m 个点,形成一条 Hamilton 路径,路径的长度就是计算量。如果能找到一条最短路径,计算量就更少。
但很遗憾$Hamilton$ 最短路问题没有多项式复杂度的解法,就算使用了状态压缩,复杂度也会达到 O(n^22^n) 这是一个天文数字。那么有没有一种算法能达到较好的结果呢?
暴力法的思路是按照坐标点 (x,y) 的 x 值来排序,它并不是一种好方法,在 y 值变化大时路径也会变得很长,如图:
这样我们显然是不能接受的,因而莫队算法提出了一个较好的排序方法。
莫队算法的思路:离线+分块+暴力
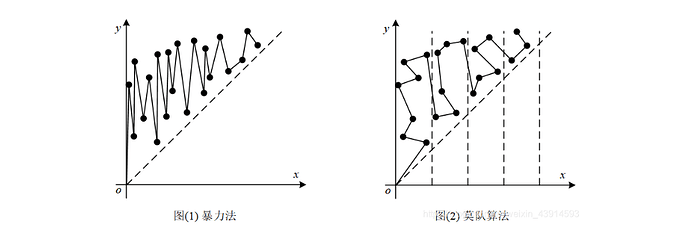
简单来说,就是把数组分块,然后把查询的区间按左端点所在的块的序号排序,如果块相同,再按右边端点排序。放图解释下(图是书上的,我不想画了)
我们发现莫队算法把暴力法 O(n) 的震动幅度降到了 O(\sqrt{n}) ,形成了一条较短的路径,从而降低了时间复杂度。具体说明参考 oiwiki
总时间复杂度 O(n\sqrt{n}) 。
代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+7;
inline int read(){
int f=1,x=0;char s=getchar();
while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();};
while(s<='9'&&s>='0'){x=x*10+s-'0';s=getchar();}
return x*f;
}
struct node{
int l,r,k;
}q[N];
int cnt[N],a[N],Ans[N],n,m,block,pos[N],ans;
inline bool cmp2(node a,node b){
return pos[a.l]^pos[b.l]?pos[a.l]<pos[b.l]:(pos[a.l]&1)?a.r<b.r:a.r>b.r;
}
void add(int x){
cnt[a[x]]++;
if(cnt[a[x]]==1) ans++;
}
void del(int x){
cnt[a[x]]--;
if(cnt[a[x]]==0) ans--;
}
int main(){
n=read();
block=sqrt(n);
for(register int i=1;i<=n;i++) {
a[i]=read();
pos[i]=(i-1)/block+1;//所属块的位置
}
m=read();
for(register int i=1;i<=m;i++) {
q[i].l=read(),q[i].r=read();
q[i].k=i;
}
sort(q+1,q+m+1,cmp2);int L=1,R=0;
for(register int i=1;i<=m;++i){
while(L<q[i].l) del(L++);
while(R>q[i].r) del(R--);
while(L>q[i].l) add(--L);
while(R<q[i].r) add(++R);
Ans[q[i].k]=ans;
}
for(register int i=1;i<=m;i++){
printf("%d\n",Ans[i]);
}
return 0;
}
顺带一提
如果把这份代码交上去,就会发现被TLE40了,没错这题特意加强了数据,即使加了一些玄学卡常也只能拿个 TLE92 ,如果有卡常大佬也可以尝试把上面代码卡过去。
这题的正解是离线+树状数组或线段树或者扫描线,都可以让时间复杂度达到 O(nlogn) 。
但不难发现,这些解法都是离线,作为一道蓝题他也不可能要求强制在线,但如果我们上点强度,强制在线,比如要求每次答案异或上次答案,那此时还没有一种在线算法可以在通过这题呢?
嘿!还真有,接下来出场的便是:
可持续化权值线段树(主席树)
主席树
浅谈一下
我们知道有很多离线算法的时间复杂度相当优秀,但如果强制在线时间复杂度就并不是那么优异。为了解决这种问题,持续化思想则给了另一种想法,即记录每个时间轴的变动,保留每个历史版本,这样我们就能维护历史版本了。
简单来说,相较于普通的数据结构,可持续化数据结构便是可以走“回头路”的。
具体实现
这题的思路是倒序建立 n 棵线段树。每棵线段树有 n 个叶子节点,第 i 个叶子节点记录第 i 个元素是否出现过。
倒序建立线段树时,每个元素都要建立一棵线段树,用 a_n 建立第一颗线段树,此时第 n 个叶子节点权值为 1 ,再用 a_{n-1} 建立第二棵线段树 ,与上一棵树连接,此时第 n-1 个叶子节点权值为 1 ,…这样第 i 棵线段树就可以表示 [n-i+1,n] 中的元素是否出现过。那如果遇到出现过的元素怎么办?我们可以通过在线段树中剔除这个重复的元素,只在最新一次出现时记录权值。
具体实现我们可以定义一个 mp[] , mp[a[i]]=i 表示 a[i] 在第 n-i+1 棵线段树中第 i 个位置出现过,当我们用 a[k] 建立线段树时,如果此时 mp[a[k]]>0 说明这个元素曾经出现过,先把第 mp[a[k]] 个叶子节点更新为 0 ,然后再把第 k 个叶子节点更新为 1 ,注意第二次更新可以直接把第一次更新的线段树覆盖就行了,并不需要重新再建立一棵线段树。(由于这题1e6的毒瘤数据加上线段树本身的大常数,所以要用 unordered\_map ,但事后发现直接开大数组好像就行了)
查询区间 [l,r] 时,由于 n-l+1 棵线段树只记录了 a_l 到 a_n 的不同数字情况,所以只需要在这棵线段树上查询 [1,r] 区间和就行了 (查询 [l,r] 也行的,但奈何常数太大只能查询 [1,r] 了,玄学优化两者相差了0.2秒)


总复杂度为 O(nlogn) ,而且是在线的。但因为线段树本身自带的大常数,在离线情况下并不如树状数组的。当然主席树还有另外一种做法,详见
//没想到吧,主席树只需要60行,码量算很小了
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+3;
int cnt,n,m,a[N],b[N],root[N];
unordered_map<int,int> mp;
inline int read(){
int f=1,x=0;char s=getchar();
while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();};
while(s<='9'&&s>='0'){x=x*10+(s-'0');s=getchar();}
return x*f;
}
inline void write(int x){
if(x<0)putchar('-'),x=-x;
if(x>9)write(x/10);
putchar(x%10+'0');
return;
}
struct tree{
int l,r,val;
}pst[N<<5];
int update(int pre,int pl,int pr,int x,int val){
int rt=++cnt;
pst[rt].l=pst[pre].l;
pst[rt].r=pst[pre].r;
pst[rt].val=pst[pre].val+val;
int mid=(pl+pr)>>1;
if(pl<pr){
if(x<=mid) pst[rt].l=update(pst[pre].l,pl,mid,x,val);
else pst[rt].r=update(pst[pre].r,mid+1,pr,x,val);
}
return rt;
}
int query(int node,int pl,int pr,int l,int r){
if(l<=pl&&pr<=r) return pst[node].val;
int res=0,mid=(pl+pr)>>1;
if(l<=mid) res+=query(pst[node].l,pl,mid,l,r);
if(mid+1<=r) res+=query(pst[node].r,mid+1,pr,l,r);
return res;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++) a[i]=read();
for(int i=n;i>=1;i--){
if(mp[a[i]]){//编号从大到小来也是可以的
root[i]=update(root[i+1],1,n,mp[a[i]],-1);//-1就是把那个节点更新为0
root[i]=update(root[i],1,n,i,1); //直接覆盖上一棵线段树就行了
}
else root[i]=update(root[i+1],1,n,i,1);
mp[a[i]]=i;
}
cin>>m;
while(m--){
int l,r;
l=read();r=read();
write(query(root[l],1,n,l,r));
putchar('\n');
}
return 0;
}