\LARGE{零:前言}
1.在本文中,“1个/所有/这个多项式”被称为f
2.如有问题或看不懂,请指出!
\LARGE{一:前置知识}
\large{1.根(零点)}
在f中,如果x=a时,f的值是0,那么把a成为f的根
做过“二分求函数的零点”的都知道,函数有零点(即此时值为0),f的根就相当于函数的零点
(根的另一种定义见“前置知识3(因式分解)
\large{2.()次方式}
a的b次方(也可以写成a^b)都见过吧?
如果把a替换成变量x这是什么?x的b次方(在f中,如果有一项是没有x的,即0次方,我们叫常数项)
在f中,可能有不同次的x,一般为了方便观察,我们把x按次数从高到低排序(像题目这样)
那么f算几次方呢?很简单,找到x的最大次数
例子:
\mathbf{x^3+3x^2+3x+1}
是一个三次方式,因为最大次数是3
\large{3.因式分解}
f这么长,怎么研究它的特点呢?——分解成小部分!这就是“因式分解”
那么我们希望分解几次式呢?——越小越好,要分解成一次式(当然,在可以分解的情况下)
最后分解结果是什么?
f=(x-a)(x-b)(x-c)… (当然,重复项要合并)
此时,”根“有了新解释:(x-a)(x-b)(x-c)中的a,b,c均为根(显然x=a/b/c时f是0)
\mathbf{这就是因式定理:}
- \mathbf{如果(x-a)是f的因子,则x为a时f为0}
- \mathbf{如果x为a时f为0,则(x-a)是f的因子)}
\large{4.如何找到可能的根}
好了,现在如果我给你一个数,你可以判断它是不是根
那可能是根的数有哪些呢?
看这个例子:x^3+2x^2-5x-6=(x-2)(x+1)(x+3),根是2,-1,-3
再看这个例子:x^3+3x^2+3x+1=(x+1)^3,根是-1,-1,-1(因为有三个)
看到规律了?
\mathbf{根(可以是负的)都是f中的常数项(最后一项)的因子}
\mathbf{证明一下:}
有乘法分配律得,拆括号时,括号内每一项都会与外面相乘,f拆括号时,常数没有x,显然是由每个括号中的常数相乘得,即每个分解出的常数必然为f常数项的因子,且这些根的积是f的常数项
\large{5.大除法}
如果你已经找到了一个正确的根,怎么将这个因式提出来呢?除法!
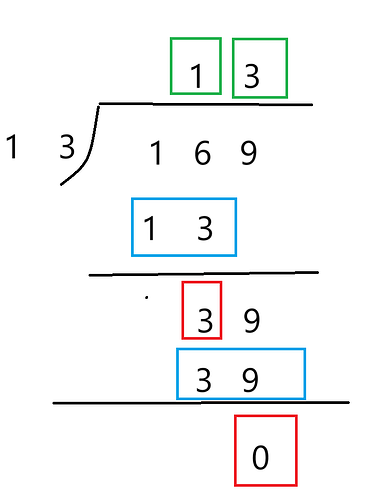
普通的除法是这样的:
分3步骤:1.试商 2.商*除数 3.求差
f的除法也是这样:
也是一样的步骤
但是,大除法
\mathbf{ 没有 满十进一!!!没有 借位!!!}
\mathbf{所有数(比如34,-2,999)都是可以的!!!}
\LARGE{二:代码实现}
看伪代码吧
不想写了
#include <bits/stdc++.h>
using namespace std;
string s;
int a[25],ans[25],n,n1,num,m,add,find_yin;//n:最大次 num:当前系数 m:当前次数 add:当前符号
bool end_ans;//find_yin:找到因子数 a:系数 ans:因子系数 end_ans:输出是否完成 n1:n的替身
void in_s(){
if(s[1]!='^'){//最高次是一次
//直接输出 记得带括号:)
end_ans=1;
return;
}
int i=2;//第3个字符开始为最高次
while(s[i]是数字){
n=n*10+(s[i]-'0');//刷新最高
i++;//下一个
}
//此时 x^n完成
n次的系数为1;
while(i<s.size()){//后面还有
if(s[i]=='+')add=1; //正负
else if(s[i]=='-')add=0;
i++;
num=0;//此时输入的系数
while(s[i]...){//找数字,同上
num=...;
i++;
}
if(add==0)num=-1*num;//正/负系数
if(i==s.size()){//无x,是常数,结束
a[0]=num;
break;
}
i++;
if(s[i]=='^'){//判断是高次 如"2x^2"
m=0;//清零
i++;
while(s[i]...){//还是找数字
m=...;
i++;
}
a[m]=num;
}
else{//是一次,如"2x"
a[1]=num;
}
}
}
void chu(int k){
for(int i=n1;i>=1;i--){
a[i-1]-=a[i]*k;//(1)a[i]:商 (2)a[i]*k:商*除数 (3) a[i-1]-=a[i]*k相减
}
for(int i=1;i<=n1;i++){
a[i-1]=a[i];//数组下标是n1-1,改为(n1-1)-0
}
n1--;//变短
}
bool check(int k){
int ss=0;
for(int i=n1;i>=0;i--){//是n1不是n!f每除一次长度缩短!
ss+=k的i次方*系数(a[i]);
}
if(...){//是根
return ...
}
else return ...;//不是
}
void find_ans(int x){//x:常数
n1=n;//n1:f此时长度
for(int i=1;i<=x;i++){
if(find_yin==n)break;//找到n个因子了
if(i是因子){
while(check(i)){//check:是不是根
ans[find_yin++]=-1*i;//相反数! a为根时因式是x-a!
chu(-1*i);//chu:大除法
}
while(check(-1*i)){ //考虑负数
ans[find_yin++]=i;
chu(i);
}
}
}
}
void out_ans(){
sort();//因式要排序 第一个ans下标是几?
int j=0,sum=0;
while(j<n){
if(ans[j]!=ans[j+1]){//与前一个不同,要输出了
if(sum==0){//没有重复的
if(ans[j]>0){//正数要加+
cout<<"(x+"<<ans[j]<<")";
}
else{//负数自带-
cout<<"(x"<<ans[j]<<")";
}
}
else{//有重复,共sum+1个相同因式(为啥是sum+1?
if(正){
...
}
else{
...
}
sum清零
}
}
else{//是重复的
...
}
找下一个,j++
}
}
int main(){
文件读写
输入字符串
处理输入:in_s()
if(一次)结束;
else{
找根:find_ans(abs(a[0]));
输出:out_ans();
}
}