10.23更新版
0.前言
各位xyd的同学们,大家好!我叫蛋小黄,对于该系列介绍见 介绍帖。
从 10.14 日起,我将更新知识点内容。
0.1 知识点分类
知识点分以下几类:
- 基础语法
- 基础算法
- 数论
- dalao专属
- 综合运用
0.2 更新顺序
每次更新指的是更新非基础语法的知识。但是,若更新基础语法,标题会变,而最上方的字不会变。
综合运用一般指的是多种知识点运用,该类一般指模拟、考试真题等。
0.3 更新内容
所有更新内容将在此处以 【Update: ??.??.??(时间) 内容】 的形式展现。
【Update:2024.10.14 发帖】
【Update:2024.10.15 增加新篇章“数论篇”以及“大佬专属篇”,将更新顺序做出改变】
【Update:2024.10.16 “排序”写了一半】
【Update:2024.10.18 数论添加第一部分“最大公因数与最小公倍数”写了一半】
【Update:2024.10.20 综合运用篇增加题目】
【Update:2024.10.23 更新基础语法一篇、基础算法一点】
1.基础语法篇
介绍:基础语法的内容将在此篇展示。
1. 头文件
C++里的头文件非常多,如:
#include <iostream>
#include <cstring>
#include <cmath>
#include <stack>
#include <queue>
#include <algorithm>
#include <map>
#include <iterator>
#include <list>
#include <cstdlib>
#include <set>
#include <ctime>
这些都是常见的头文件。
如果不想打这么多的字符,建议使用#include <bits/stdc++.h>,也就是我们常说的“万能头”,包含了C++中绝大多数头文件。
但是,在一些比赛中,是不允许使用万能头文件的,所以大家在感受万能头的方便时,也需要背一些常见头文件。
2. 数据类型
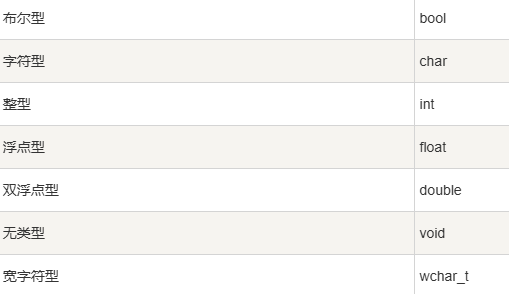
C++中,有很多不同的数据类型。常见的有整型、浮点型、字符型、字符串型、布尔型。
以下的表格,左边为数据类型,右边为关键字。
2.基础算法篇
介绍:基础算法的所有内容将在此篇展示,这是一个漫长的篇章…
2.1 算法开篇—排序
我们不在此篇介绍过多排序,只介绍一些简单、实用的排序。
排序算法 (英语:Sorting algorithm)是一种将一组特定的数据按某种顺序进行排列的算法。排序算法多种多样,性质也大多不同。
2.1.0 排序算法的稳定性
排序算法的稳定性 是指相等的元素经过排序之后相对顺序是否发生了改变。
拥有稳定性这一特性的算法会让原本有相等键值的纪录维持相对次序,即如果一个排序算法是稳定的,当有两个相等键值的纪录 R 和 S ,且在原本的列表中 R 出现在 S 之前,在排序过的列表中 R 也将会是在 S 之前。
2.1.1 桶排序
桶排序按下列步骤进行:
- 设置一个定量的数组当作空桶;
- 遍历序列,并将元素一个个放到对应的桶中;
- 对每个不是空的桶进行排序;
- 从不是空的桶里把元素再放回原来的序列中。
而桶排序一般适用于待排序序列分布较均匀的情况。
对于桶排序,没学过 STL 模版库的兄弟们就只能用数组了(缺点:容量太小啦!),不过学过的人都知道,我们可以使用 map 来记录。
map/set的分享,可看。
2.2 贪心算法
引入
现在我们考虑买东西付 37块钱,现在你有 1元钞票,5元钞票,10元钞票与 20元钞票,都有无限个,请问要付最少的钞票你要付多少张钞票?
很明显,这道题的策略就是尽量选大钞票,37=201+101+51+12。
所以,这就是你的贪心策略。
2.2.1 贪心算法定义
贪心算法(英语:greedy algorithm),是用计算机来模拟一个「贪心」的人做出决策的过程。这个人十分贪婪,每一步行动总是按某种指标选取最优的操作。而且他目光短浅,总是只看眼前,并不考虑以后可能造成的影响。
可想而知,并不是所有的时候贪心法都能获得最优解,所以一般使用贪心法的时候,都要确保自己能证明其正确性。
2.2.1 如何解决贪心问题
首先,我们需要定一个“贪心策略”,随后我们证明其贪心策略正确。
如何证明?
一般来说,我们可以大胆猜测,举几个例子,如果都可以,就大胆去写。如果有反例,再重新想。
3.数论篇
介绍:本篇为数学相关知识,我们称为数论。
3.1 最小公因数与最大公倍数
在小学时,我们就知道有这样两个表两数或多数关系的东东,名最小公因数与最大公倍数。
不过,我深刻记得当时学这玩意是为了约分与通分。
3.1 0 定义
最大公因数(英语:greatest common divisor,gcd)。是数学词汇,指能够整除多个整数的最大正整数。而多个整数不能都为零。
最小公倍数(英语: Least Common Multiple,lcm)。是数学词汇,指多个整数能够整除的最小正整数。而多个整数不能为零。
3.3.1 求最大公因数
如果我们已知两个数 a 和 b ,且 a>b ,如何求出二者的最大公约数呢?
我们发现如果 b 是 a 的约数,那么 b 就是二者的最大公约数。 下面讨论不能整除的情况,即 $a=b*q+r$,其中 r<b 。
我们可以得到 gcd(a,b)=gcd(b,a mod b) ,如下。

也就是 gcd(a,b)=gcd(b,r)。
这就是求最大公因数的递归方式。
4.大佬专属篇~~
介绍:大佬总是爱提意见,随他们愿
4.0 本篇致辞
由于我有些也不会,所以OI-WiKi 非常重要!!!!!
4.1 LCT
dalao为:@陶荣杰1
嗯…
LCT是what? 这事得问陶xx
LCT,全称 Link/Cut Tree ,是一种数据结构,我们用它来解决 动态树问题 。
你说什么?啥是动态树问题?这事得问陶xx
4.1.0 动态树问题
维护一个 森林,支持删除某条边,加入某条边,并保证加边,删边之后仍是森林。我们要维护这个森林的一些信息。
一般的操作有两点连通性,两点路径权值和,连接两点和切断某条边、修改信息等。
4.1.1 引入
维护一棵树,支持如下操作:
- 修改两点间路径权值。
- 查询两点间路径权值和。
- 修改某点子树权值。
- 查询某点子树权值和。
- 断开并连接一些边,保证仍是一棵树。
本题目如果不存在最后一条件,那也是非常的简单(对于提高组),不过存在其条件,所以我们需要使用 LCT。(这题得问陶xx)
4.1.2 LCT
我们可以简单的把 LCT 理解成用一些 Splay 来维护动态的树链剖分,以期实现动态树上的区间操作。对于每条实链,我们建一个 Splay 来维护整个链区间的信息。
4.1.3 构建辅助树
你可以认为一些 Splay 构成了一个辅助树,每棵辅助树维护的是一棵树,一些辅助树构成了 LCT,其维护的是整个森林。
- 辅助树由多棵 Splay 组成,每棵 Splay 维护原树中的一条路径,且中序遍历这棵 Splay 得到的点序列,从前到后对应原树「从上到下」的一条路径。
- 原树每个节点与辅助树的 Splay 节点一一对应。
- 辅助树的各棵 Splay 之间并不是独立的。每棵 Splay 的根节点的父亲节点本应是空,但在 LCT 中每棵 Splay 的根节点的父亲节点指向原树中 这条链 的父亲节点(即链最顶端的点的父亲节点)。这类父亲链接与通常 Splay 的父亲链接区别在于儿子认父亲,而父亲不认儿子,对应原树的一条 虚边。因此,每个连通块恰好有一个点的父亲节点为空。
- 由于辅助树的以上性质,我们维护任何操作都不需要维护原树,辅助树可以在任何情况下拿出一个唯一的原树,我们只需要维护辅助树即可。
4.1.4 时间复杂度
LCT 中的大部分操作都基于 Access,其余操作的时间复杂度都为常数,因此我们只需要分析 Access 操作的时间复杂度。
其中,Access 的时间复杂度主要来自于多次 splay 操作和对路径中虚边的访问,接下来分别分析这两部分的时间复杂度。
—————————————————————————————————————————————
P3203 [HNOI2010] 弹飞绵羊 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
int main(){
register char ch;
R n,m,j,k;
in(n);
for(j=1;j<=n;++j){
s[j]=1;
in(k);
if(j+k<=n)f[j]=j+k;//如果弹飞了就不连边
}
in(m);
while(m--){
gc;
if(ch&1){
in(j);++j;
access(j);splay(j);//直接查询
printf("%d\n",s[j]);
}
else{
in(j);in(k);++j;
access(j);splay(j);
c[j][0]=f[c[j][0]]=0;//直接断边
if(j+k<=n)f[j]=j+k;//直接连边
pushup(j);
}
}
return 0;
}
虽然我知道大佬们故意为难我,但我就要讲
5.综合运用篇
介绍:本篇具体分为:大模拟、CSP/NOIP真题、其余真题。
5.1 NOIP 篇(普及组)
5.1.1 NOIP1997
洛谷在NOIP1997只有一题,就讲你啦!
P1548 [NOIP1997 普及组] 棋盘问题
学过小学奥数的都知道系列
我们都知道,小学奥数有教过,一个长方形,以递归的方式,每次都加他的长*宽,每次都让他们俩减1,知道有一个数为 0。
以函数形式是这么写的:
int f(int x,int y,int sum){ //x=长,y=宽,sum=之前全部的总和
if(x==0||y==0){
return sum;
}
sum+=x*y;
return f(x-1,y-1,sum);
}
随后是长方形,依旧是学过小学奥数都知道,长方形的个数为 ((m+1)*(n+1)*m*n)/4。其中 m,n 分别为长宽。
于是,结果就出来了。水过一期
材料引用(感谢致辞):
OI wiki(官网)
