(闲的没事干)
[求大佬指正!感谢!]
目录:
1.树
2.栈
3.队列
4.串
5.数组
6.图
7.哈希表
8.链表
(进入正文)
树(tree)
1.树的概念
树由根、节点组成,与生活中的树长得非常像。与现实不同的是,这家伙是倒过来的。
A
/ \
B C
/ \
D E
/ \
F G
2.树的存储结构
树的存储结构有两种,分别是数组储存和链表储存,数组储存时孩子节点和父亲节点的下标之间存在一定关系,可以相互表示;链表实现就是使用指针指孩子节点了。
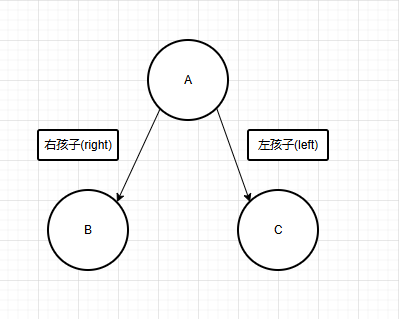
a.双亲表示法(仅能二叉树使用)
左指针指向的就是左孩子,右指针指向的就是右孩子,当然孩子可能有多个,定义对应数量的节点指针即可。
typdef struct node{
struct node* left;
struct node* right;
int value;
}node;
b. 孩子兄弟表示法
每个节点的指针指向孩子的和兄弟。
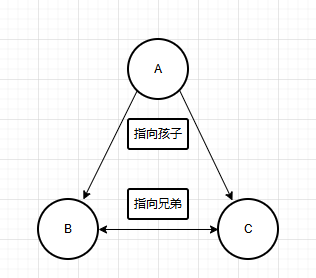
typdef struct node{
struct node* child;
struct node* brother;
int value;
}node;
3.二叉树
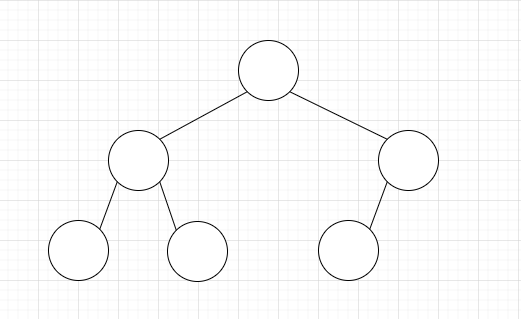
a.完全二叉树
除了最后一层可能不满其他层都满。
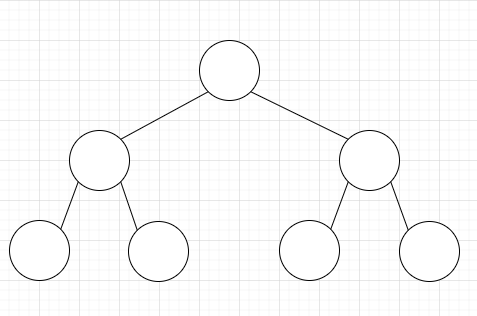
b.满二叉树
满层都满。
c.二叉树之代码
node make(node* r,int value){//创造节点
if(r==nullptr)return new node(value);
if(value < r->value)r->left=make(r->left,value);
else r->right=make(r->right,value);
}
d.二叉树之遍历
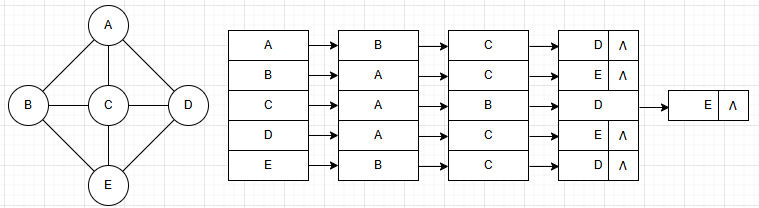
(1).前序遍历
一句话:“先根后孩子”。
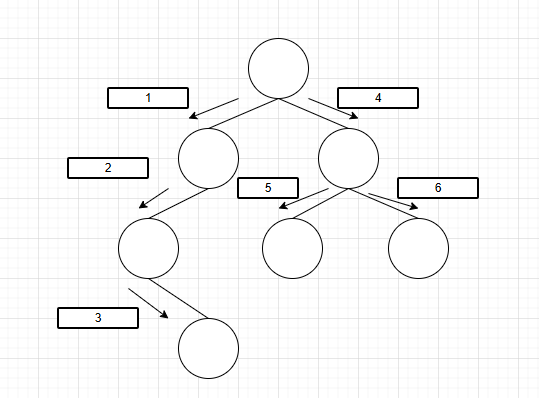
如图所示
void pre(node* r){
if (r==nullptr)return;
cout<< r->value<<endl;
pre(r->left);
pre(r->right);
}
(2).中序遍历
“左孩子-根-右孩子”
void pre(node* r){
if (r==nullptr)return;
pre(r->left);
cout<< r->value<<endl;
pre(r->right);
}
(3).后序遍历
“后根,先孩子”
void pre(node* r){
if (r==nullptr)return;
pre(r->left);
pre(r->right);
cout<< r->value<<endl;
}
栈(stack)
1.栈的概念
我们可以把栈看作是一个容器,只允许:1.把东西放进栈顶;2.把东西从栈顶取出
元素↑↓
| |
| |
| |
| |
|______|
2.栈的操作
特别好记,就几种:
a.压入(push)
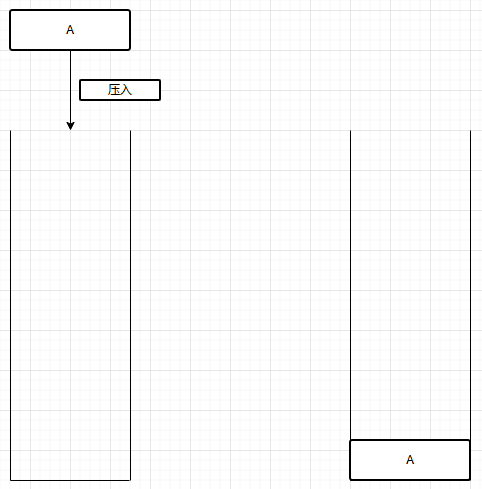
b.弹出(pop)
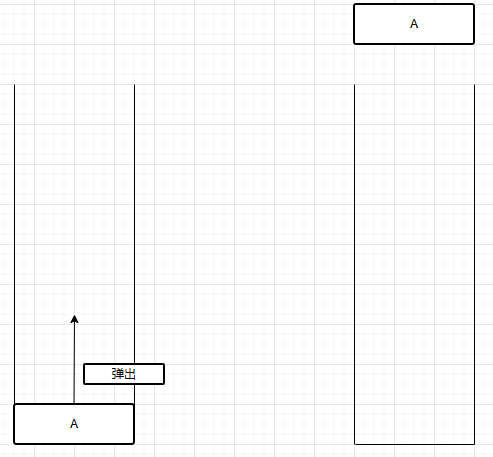
c.看栈顶元素(peek)
d.判断是否为空(empty?)
e.栈的大小(size)
3.栈的基本操作(STL)
stack<int> s;//声明栈
s.push(1);//压入1
s.pop();//弹出栈顶元素
s.top();//栈顶元素
s.size();//栈的内部元素个数
s.empty();//判断是否为空
队列(queue)
1.队列基本概念
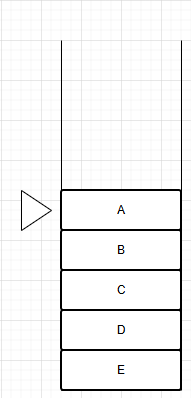
队列就像个筒一样,只能从顶端压入东西,从底部取出东西。
元素↓ (尾部)
| |
| |
| |
| |
元素↓ (头部)
2.队列的操作
a.入队(push)
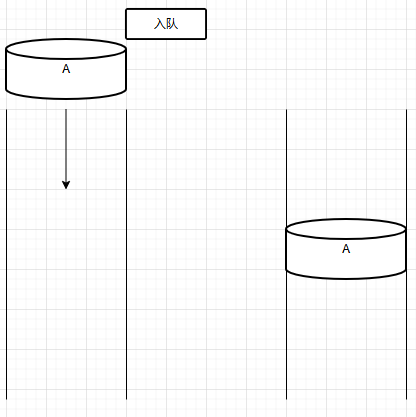
b.出队(pop)
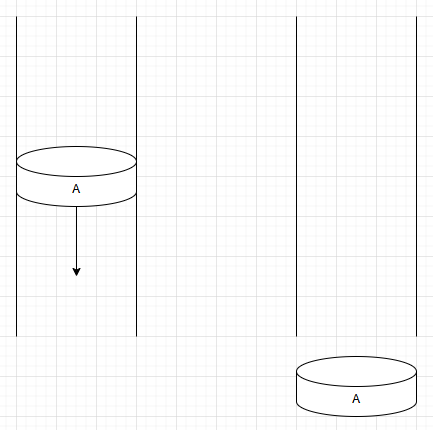
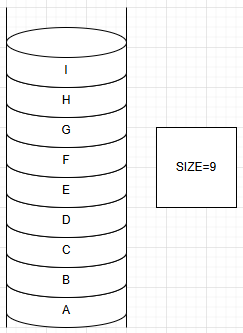
c.队列中元素个数(size)
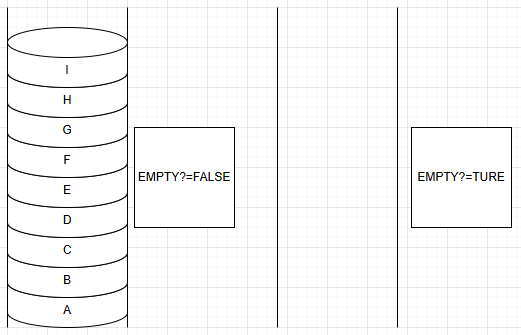
d.判断数列是否为空(empty?)
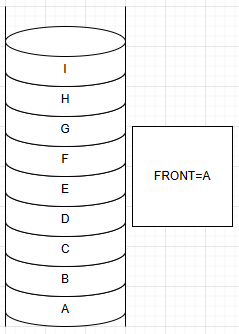
e.返回队首元素(front)
3.队列之实现(STL)
queue<int> q;//声明一个队列
q.push(10);//添加元素
cout<<q.front()<<endl;//输出队首元素
cout<<q.empty()<<endl;//判断队列是否为空
cout<<q.size()<<endl;//输出队列中元素个数
q.pop();//出队
串(string)
1.串的概念
是一种特殊的线性表,是由零个或多个字符组成的有限序列,强调了只能由字符组成,可以是字母、数组、符号等组成。
A&%***BCCCXY(^@!@***#
2.串的基本操作
a.赋值(assign)
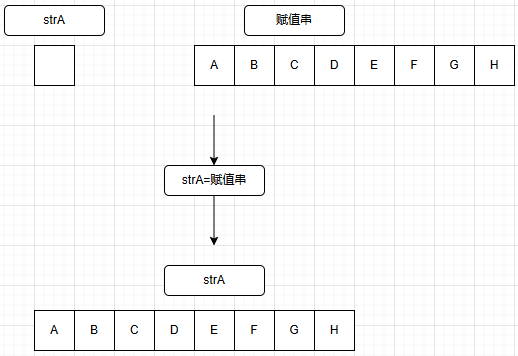
b.复制(copy)
c. 判空操作(empty?)

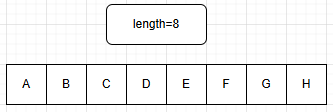
d. 求串长操作(length)
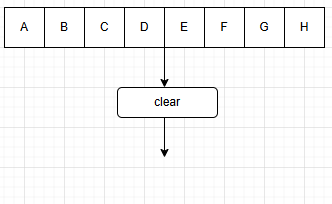
e.清空操作(clear)
f. 销毁操作(destroy)
g. 串联接操作(concat)
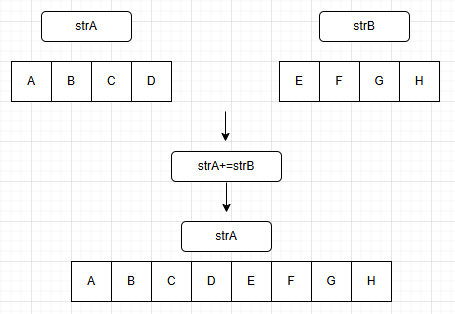
h. 求子串操作(substring)
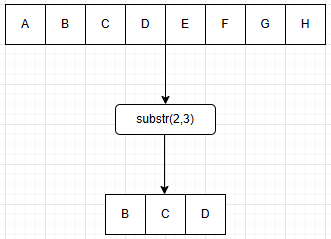
i. 定位操作(index)
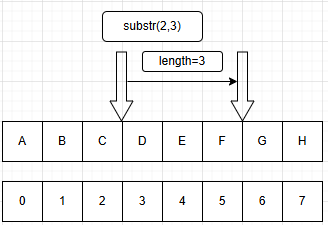
j. 比较操作(compre)
3.串的实现
string s,a,b;//字符串
s+=a;//连接
s="fasdgfasdfasfasfasdfasfdafsdfd";//赋值
cout<<s.length==0<<endl;//判断是否为空
cout<<s.size()<<endl;//长度
str1.replace(6, 5, "C++");//替换
if (str1.find("fas") != std::string::npos) {//查找
std::cout << "Found fas in the string!" << std::endl;
}
cout<< a > b <<endl;//比较
数组(array)
1.数组基本概念
存储一个固定大小的相同类型元素的顺序集合。数组中的元素可以通过索引访问,索引通常从0开始。
元素 1 8 6 4 9 2 7
索引 1 2 3 4 5 6 7
2.数组的基本操作
a.访问
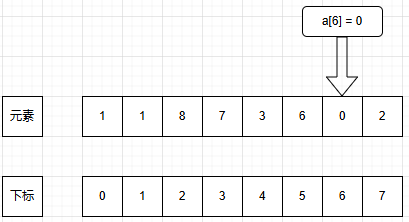
b.赋值

这些就是最基本的数组的操作了。
2.数组实现
int a[10];//声明
a[0]=1;//赋值
a[1]=3;
for(int i=0;i<10;i++){//访问并输出
cout<<a[i]<<endl;
}
图
1.图的概念
图是由顶点集合及顶点间的关系组成的一种数据结构 ,通常表示为[G = (V, E)],其中[V]是顶点集合,是顶点间关系的有穷集合,也叫做边的集合。
A
/|\
/ | \
B--C--D
\ | /
\|/
E
2.图的存储方式
a.邻接表
可以存储每个节点的相同的节点
#include <iostream>
#include <list>
#include <vector>
using namespace std;
typedef struct Edge {
int dest;
int weight;
};
class Graph {
int V;
list<Edge> *adj;
public:
Graph(int V) {
this->V = V;
adj = new list<Edge>[V];
}
void addEdge(int src, int dest, int weight) {
Edge edge = {dest, weight};
adj[src].push_back(edge);
}
void printAdjList() {
for (int i = 0; i < V; ++i) {
cout << "Vertex " << i << " -> ";
list<Edge>::iterator itr;
for (itr = adj[i].begin(); itr != adj[i].end(); ++itr) {
cout << "[" << itr->dest << ", " << itr->weight << "] -> ";
}
cout << "NULL" << endl;
}
}
};
int main() {
Graph g(5);
g.addEdge(0, 1, 10);
g.addEdge(0, 4, 30);
g.addEdge(1, 2, 10);
g.addEdge(1, 3, 20);
g.addEdge(1, 4, 40);
g.printAdjList();
return 0;
}
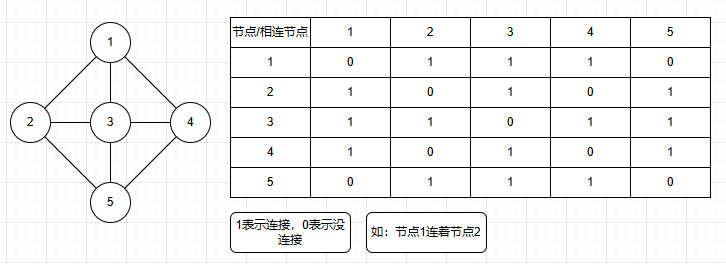
b.邻接矩阵
邻接表的变异版本(可以这么说吧),a[n][m]表示n节点下,用m表示,1为m是n的相连节点,0不是。
#include <iostream>
#include <vector>
using namespace std;
class Graph {
int V; // 顶点数
vector<vector<int>> adj; // 邻接矩阵
public:
Graph(int V) {
this->V = V;
adj.resize(V, vector<int>(V, 0)); // 初始化邻接矩阵
}
void addEdge(int v, int w) {
adj[v][w] = 1; // 无向图需要设置两次
adj[w][v] = 1;
}
void display() {
for (int i = 0; i < V; ++i) {
for (int j = 0; j < V; ++j)
cout << adj[i][j] << " ";
cout << endl;
}
}
};
int main() {
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
cout << "邻接矩阵为:" << endl;
g.display();
return 0;
}
3.图的类型
a.有向图
边又向。(有向边)
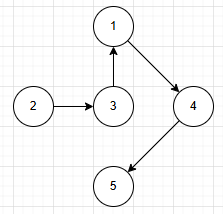
b.无向图
边无向。(无向边)
c.简单图
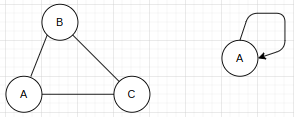
既不含平行边也不含环的图称为简单图。
![]()
d.完全图
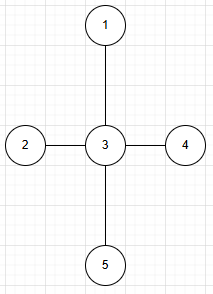
在无向图中,若任意两个点都有一条边,则该图称为无向完全图。
e. 稀疏图
有很少边或弧的图称为稀疏图。
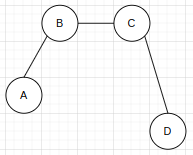
f.稠密图
与稀疏图的特点相反。
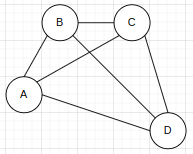
g.网
带权的图称为网。
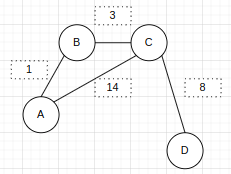
4.其他概念
a.度
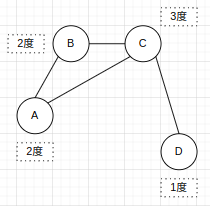
b.子图
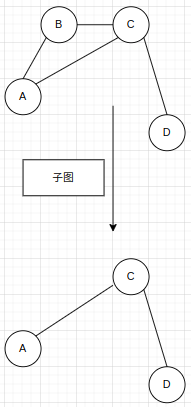
c. 连通图和连通分量
连通图:在无向图中,如果顶点vi到vj有路径,则称vi和vj是连通的。如果图中任何两个顶点都是连通的,则称G为连通图。
连通分量:无向图G的极大连通子图称为G的连通分量。极大连通子图意思是:该子图是G的连通子图,如果再加入一个顶点,该子图不连通。
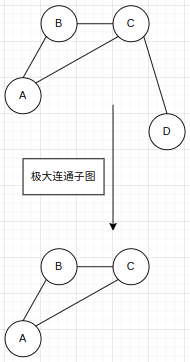
d. 强连通图和强连通分量
强连通图:在有向图中,如果图中任何两个顶点vi到vj有路径,且vj到vi也有路径,则称G为强连通图。
强连通分量:有向图G的极大强连通子图称为G的强连通分量。极大强连通子图意思是:该子图是G的强连通子图,如果再加入一个顶点,该子图不再是强连通的。
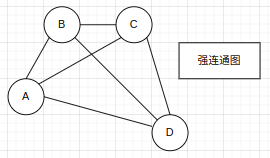
哈希表
1.哈希表的概念
哈希表(Hash table,也叫散列表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以此来加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫散列表。
哈希表有多种不同的实现方式,但是在C++中最常用的是用开放地址法来处理冲突。开放地址法中有一种方法是线性探测,这种方法的基本思路是:当关键字key的散列地址发生冲突时,按照某种规则(比如线性规则)求得下一个散列地址,如果仍然冲突,继续求得下一个散列地址,直到找到一个不冲突的散列地址为止。
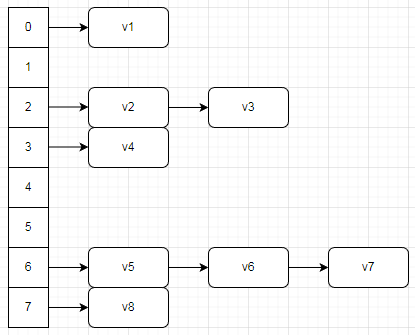
2.哈希表基本操作及代码实现
#include <iostream>
#include <functional> // std::hash
#include <unordered_map> // std::unordered_map
int main() {
// 创建一个unordered_map实例
std::unordered_map<int, std::string> myMap;
// 插入元素
myMap[1] = "one";
myMap[2] = "two";
myMap[3] = "three";
// 查找并访问元素
if (myMap.find(2) != myMap.end()) {
std::cout << "Found: " << myMap[2] << std::endl;
}
// 迭代访问元素
for (const auto& pair : myMap) {
std::cout << pair.first << ": " << pair.second << std::endl;
}
// 删除元素
myMap.erase(2);
// 计算键的哈希值
std::size_t hashValue = std::hash<int>()(1);
std::cout << "Hash value of key 1: " << hashValue << std::endl;
return 0;
}
链表
1.链表概念
链表是一种在物理存储单元上非连续、非顺序的数据结构,由一系列节点组成。每个节点包含两个部分:数据域和指针域数据域用于存储数据元素,指针域用于指向下一个节点。链表的逻辑顺序通过节点的指针链接次序实现。
2.链表的类型
a.单链表
![]()
b.双链表
c.循环链表

3.链表的实现
#include <iostream>
// 定义链表节点
class Node {
public:
int data;
Node* next;
Node(int val) : data(val), next(nullptr) {}
};
// 定义链表类
class LinkedList {
private:
Node* head;
public:
LinkedList() : head(nullptr) {}
// 向链表添加元素
void append(int value) {
if (!head) {
head = new Node(value);
} else {
Node* current = head;
while (current->next) {
current = current->next;
}
current->next = new Node(value);
}
}
// 显示链表所有元素
void display() {
Node* current = head;
while (current) {
std::cout << current->data << " -> ";
current = current->next;
}
std::cout << "null" << std::endl;
}
// 删除链表
~LinkedList() {
while (head) {
Node* next = head->next;
delete head;
head = next;
}
}
};
int main() {
LinkedList list;
// 添加元素
list.append(1);
list.append(2);
list.append(3);
// 显示链表
list.display(); // 输出: 1 -> 2 -> 3 -> null
return 0;
}
-------------------------------------------------------------- -----------------------------------------------------------------
-----------------------------------------------------------------