姓名: 吴苏韬
赛道: 提高组
类型: 算法技能
Splay
关键词: Splay,平衡树
Splay 树
定义
Splay 树是一个二叉平衡搜索树,它可以通过 Splay 操作 将一个结点旋转至根结点或者一个给定的结点的下一层,使得整棵树仍然满足二叉搜索树的性质。
Splay 树可以在均摊 O(\log n) 的时间内完成查找、插入、查询、删除等操作。
二叉搜索树的定义:
- 空树是一个二叉搜索树;
- 根结点左子树中的结点权值均小于根结点的权值;
- 根结点右子树中的结点权值均大于根结点的权值;
- 根结点的左右子树均为二叉搜索树。
结构
在 Splay 中,一共需要维护如下信息:
root:树的根结点编号。tot:当前总共开了点的个数(Splay 树显然使用动态开点)。fa[i]:结点 i 的父亲结点。son[i][0/1]:结点 i 的左右儿子编号,左儿子为son[i][0],右儿子为son[i][1]。val[i]:结点 i 的权值。cnt[i]:权值为val[i]的数字的出现个数。siz[i]:结点 i 及其子树的大小。
基本操作
辅助函数
pushup(x):合并左右儿子的信息(即大小),更新至当前结点。get(x):返回 0 表示 x 是父结点的左儿子,返回 1 表示 x 是父结点的右儿子。clear(x):销毁结点 x ,即将一切信息清零。
void pushup(int x) { // 合并 x 的左儿子与右儿子,得到 x 的大小
siz[x] = siz[son[x][0]] + siz[son[x][1]] + cnt[x];
}
bool get(int x) { // get(x)=1 说明 x 是右儿子,反之是左儿子
return x == son[fa[x]][1];
}
void clear(int x) { // 销毁结点 x
son[x][0] = son[x][1] = fa[x] = val[x] = siz[x] = cnt[x] = 0;
}
旋转
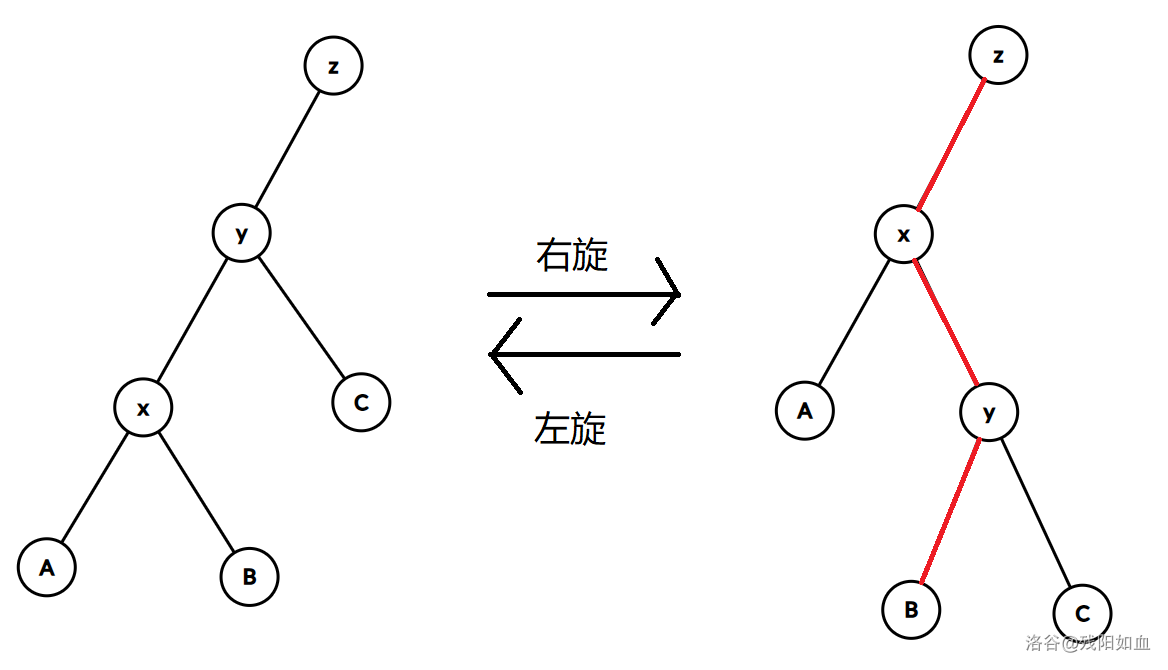
左旋是右旋的逆操作,所以下面只讨论右旋。
旋转操作如上图。
可以发现,右旋是把 x 提到 z 的下面然后把 y 压下去,此时由于 x 有有儿子了,所以如图可以想象成 B 不动,此时就接到了 y 的下面(胡思乱想中)。
实际把图片记住就行了,上面扯一大通 P 用没有
在右旋中,我们需要知道 x 的父亲结点和爷爷结点,所以
int y = fa[x], z = fa[y];
然后我们还需要知道 x 是 y 的左儿子还是右儿子,如果 x 是左儿子就右旋,反之左旋。
int id = get(x); // 判断 x 是 y 的左儿子还是右儿子
容易发现,在右旋中,改变的边的关系只有 x-z , x-y , y-B ,所以我们分别考虑。
修改为 x-z
由于 x 替换掉的是 y 的位置,所以需要先知道 y 是 z 的哪个儿子,故先 get(y)。
当 z 点不存在时(即 z=0 ),那么更新 son[z] 会发生错误,因为访问的时候一般是用是否为 0 判断点是否存在。若 z 为根结点,那么就会遍历下去导致错误的答案。
而 x 必然存在,无需判断。
if (z) son[z][get(y)] = x;
fa[x] = z;
修改为 x-y
由于右旋保证了 y 是存在的,所以两种情况都无需判断。
son[x][id ^ 1] = y, fa[y] = x;
修改为 y-B
B 是 x 的右儿子,而 x 是 y 的左儿子,所以发现 B 就是 son[x][id ^ 1]。
同理此时 B 不一定存在,所以也需要判断。
son[y][id] = son[x][id ^ 1];
if (son[x][id ^ 1]) fa[son[x][id ^ 1]] = y;
完整代码
void rotate(int x) {
int y = fa[x], z = fa[y];
int id = get(x); // 判断 x 是 y 的左儿子还是右儿子
if (z) son[z][get(y)] = x;
fa[x] = z;
son[y][id] = son[x][id ^ 1];
if (son[x][id ^ 1]) fa[son[x][id ^ 1]] = y;
son[x][id ^ 1] = y, fa[y] = x;
pushup(y), pushup(x);
}
Splay 操作
Splay 操作规定:每操作(包括但不限于插入、删除,详见代码)一个结点 x 后,都要将这个节点 x 旋转为结点 k 的儿子,若 k=0 则将其旋转至根结点。
根据定义,当 fa[x] != k 时,需要一直向上旋转,故写一个 while 循环。
特殊型
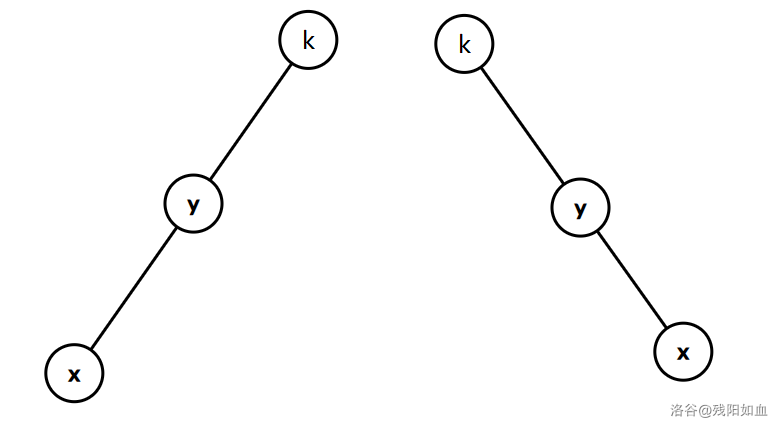
如图, k 是 x 的爷爷结点,此情况称为特殊型。
对于这两种情况,我们只需要将 x 点分别左旋、右旋,就可以让 x 顶替掉 y 的位置,成为 k 的儿子。
同构型
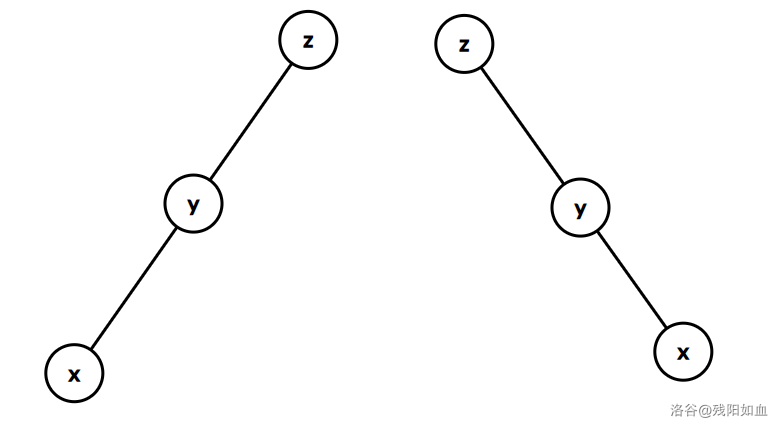
如图,当 x 的爷爷节点非 k ,且 x,y,k 三点共线时,此情况称为同构型。
此时我们的目标是让 x 顶替掉 $z$ ,成为这一条链中深度最浅的链头。
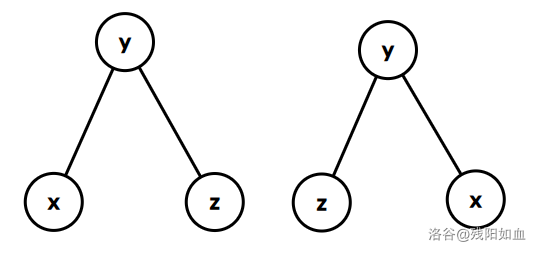
首先,我们将 y 点旋转,此时 y 成为深度最浅的结点,同时 x,z 是 y 的两个儿子。
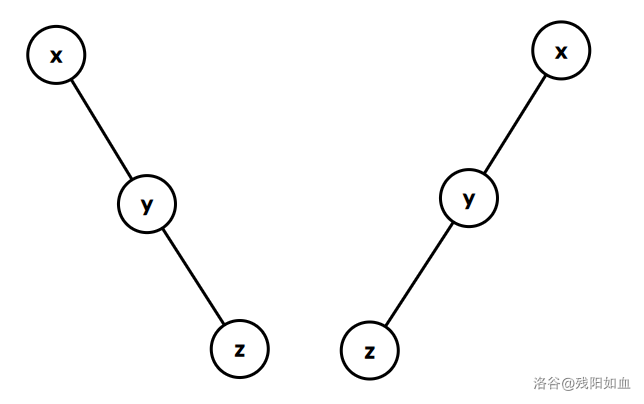
然后我们将 x 点旋转,让 x 成为 y 的父亲,此时 x 就成为了深度最浅的点,操作完成。
总结:对于同构型,先旋转 y ,再旋转 x 。
异构型
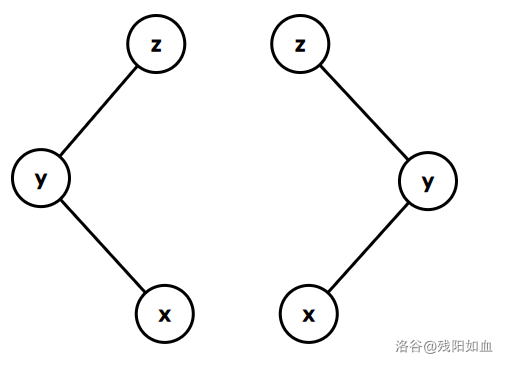
如图,当 x 的爷爷结点非 k ,且 $x,y,z$ 三点构成折线时,此情况称为异构型。
此时我们的目标同样是让 x 顶替掉 z , 成为这一条链中深度最浅的链头。
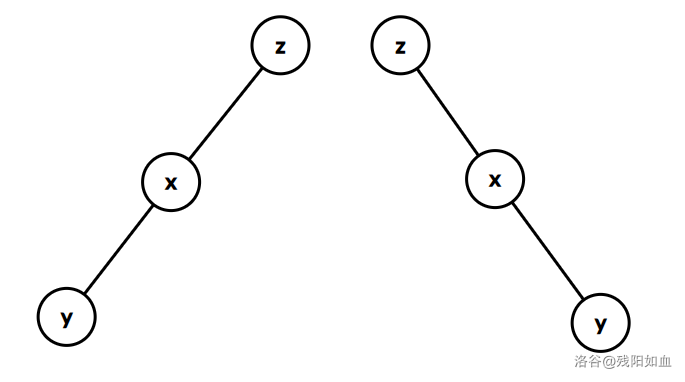
首先,我们将 x 点旋转,此时 x 称为 z 的儿子,三点共线。
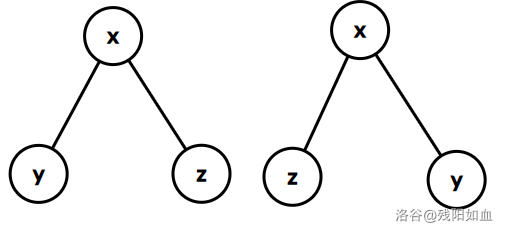
然后我们再次将 x 点旋转, z 称为 x 的儿子,此时 $x$ 就成为了深度最浅的点,操作完成。
总结:对于异构型,先旋转 x ,再旋转 $x$ 。
代码实现
发现无论对于哪种情况,最后都会旋转一次 x ,所以可以将这一次操作提取出来。
如何判断三点是同构还是异构呢?可以用 $\text{get}(x)\oplus\text{get}(y)$ 获得。
具体实现详见代码。
判断同构、异构的解释
同构
此时 x 是 y 的左(右)儿子,y 是 z 的左(右)儿子,儿子左右情况相同,那么 \text{get}(x)=\text{get}(y),异或值为 0 。
异构
此时 x 是 y 的左(右)儿子,y 是 z 的右(左)儿子,儿子左右情况不同,那么 \text{get}(x)\not=\text{get}(y),且一个为 0 一个为 1,故异或值为 1。
void splay(int x, int k) { // 将 x 转到 k 的下面
while (fa[x] != k) {
int y = fa[x], z = fa[y];
if (z != k) {
if (get(x) ^ get(y)) rotate(x); // 异构
else rotate(y); // 同构
}
rotate(x);
}
if (!k) root = x;// 若旋转为根结点,那么将根结点 root 设为 x
}
时间复杂度分析
本部分来自 OI-wiki。
考虑对 Splay 操作中的三种情况分析复杂度。采用势能分析,定义一个 n 个节点的 Splay 树进行了 m 次 Splay 操作。
可记 w(x)=\left\lfloor\log\text{size}_x\right\rfloor ,定义势能函数为 \varphi=\sum w(x) ,其中 \varphi(0)\le n\log n 。
在第 i 次操作后势能为 \varphi(i) ,则我们只需求出初始势能和每次的势能变化量的和即可。
-
特殊型:势能变化量为
\begin{aligned} &1+w'(x)+w'(y)-w(x)-w(y)\\ \le\,&1+w'(y)-w(x)\\ \le\,&1+w'(x)-w(x) \end{aligned} -
同构型:势能变化量为
\begin{aligned} &1+w'(x)+w'(y)+w'(z)-w(x)-w(y)-w(z)\\ \le\,& 1+w'(y)+w'(z)-w(x)-w(y)\\ \le\,& 1+w'(x)+w'(z)-2w(x)\\ \le\,& 3\big(w'(x)-w(x)\big) \end{aligned} -
异构型:势能变化量为
\begin{aligned} &1+w'(x)+w'(y)+w'(z)-w(x)-w(y)-w(z)\\ \le\,& 1+w'(y)+w'(z)-w(x)-w(y)\\ \le\,& 1+w'(z)+w'(y)-2w(x)\\ \le\,& 2w'(x)-w'(z)-w'(y)+w'(z)-w(x)-w(y)\\ \le\,& 2\big(w'(x)-w(x)\big) \end{aligned}
由此可见,三种操作的势能全部可以缩放为 \le 3\big(w'(x)-w(x)\big) 。
令 w^{(n)}(x)=w'^{(n-1)(x)} , w^{(0)}(x)=w(x) ,Splay 操作一次依次访问了 x_1,x_2,\cdots,x_n ,最终 x_1 成为深度最浅的结点,那么可得:
继而可得:
因此,对于 n 个结点的 Splay 树,做一次 Splay 操作的均摊复杂度为 O(\log n) 。
因此基于 Splay 的操作的时间复杂度也是均摊 O(\log n) 的。
应用 1:维护一个集合
例题:#104. 普通平衡树 - 题目 - LibreOJ (loj.ac)
插入
由于二叉搜索是递归定义的,所以可以用递归的思想考虑(假设插入值为 k ):
- 如果当前结点为空,那么就新建一个结点存储当前值。
- 如果当前结点的权值等于 k,那么更新当前结点的计数器并且更新当前结点与父亲的大小。
- 若 k 小于权值就进入左子树,大于权值就进入右子树。
注意,最后更新/新建结点之后,必须执行 Splay 操作,否则时间复杂度不正确!
void insert(int k) {
if (!root) { // 树为空,新建节点
val[++tot] = k;
++cnt[tot];
root = tot;
pushup(root); // 更新大小
return ;
}
int x = root, y = 0;
while (true) {
if (val[x] == k) { // 找到目标
++cnt[x]; // 更新计数器
pushup(x), pushup(y);
splay(x, 0); // 旋转至根结点
break;
}
y = x, x = son[x][val[x] < k]; // 进入子树
if (!x) { // 到了空结点,插入新结点
val[++tot] = k;
++cnt[tot];
fa[tot] = y;
son[y][val[y] < k] = tot; // 根据二叉搜索树的性质插入
pushup(tot);
pushup(y);
splay(tot, 0);
break;
}
}
根据权值查询排名
假设当前给定的权值为 k,要查找 $k$ 的排名。
维护一个 \text{res} 统计当前已经计算了权值小于 k 的结点个数。
-
当前结点为空,返回 \text{res}+1 。
-
k 小于当前结点的权值,那么进入当前结点的左子树查找,无需更新 \text{res} 。
-
$k$ 大于等于当前结点的权值
那么当前结点的左子树中的结点都小于 k,
res += siz[son[x][0]],加上左子树的大小。如果 k 等于当前结点的权值,那么将其旋转至根结点,返回 \text{res}+1 。
如果 k 大于当前结点的权值,那么当前结点的权值也小于 k 了,
res += cnt[x],同时进入右子树。
int get_rank(int k) { // 查询 k 的排名
int res = 0, x = root;
while (true) {
if (k < val[x]) x = son[x][0]; // k 落在 x 的左子树
else {
res += siz[son[x][0]]; // 加上左子树的大小
if (!x) return res + 1; // 当前结点为空
if (val[x] == k) return splay(x, 0), res + 1; // 当前结点权值等于 k
res += cnt[x], x = son[x][1]; // 进入右子树
}
}
return -1;
}
根据排名查询权值
假设当前要查询排名为 $k$ 的数,但是在下面,k 是实时维护的。
-
如果
k <= siz[son[x][0]],那么排名为 k 的数就在左子树中,进入左子树即可。 -
否则让
k -= cnt[x] + siz[son[x][0]],相当于减去根结点的数量和左子树大小。-
如果此时 k\le 0 ,那么说明
siz[son[x][0]] < k <= cnt[x],即排名为 k 的数就是当前结点。将其旋转至跟节点后返回即可。 -
否则进入右子树。
-
int get_kth(int k) { // 查询排名为 k 的数
int x = root;
while (true) {
if (son[x][0] && k <= siz[son[x][0]]) x = son[x][0]; // 进入左子树
else {
k -= cnt[x] + siz[son[x][0]]; // 减去根结点的数量和左子树大小
if (k <= 0) return splay(x, 0), val[x]; // 说明 siz[son[x][0]] < k <= cnt[x]
x = son[x][1]; // 进入右子树
}
}
return -1; // 找不到,即树的大小 < k
}
查询根结点的前驱/后继
至于为什么要查询根结点的前驱/后继,将会在后面的操作中给出解释。
如果想要查找一个任意权值 k 的前驱/后继,只需先将 k 插入树中。
由于插入函数中执行了 splay,所以此时 $k$ 就位于根结点的位置,可以直接调用函数。
查询完之后删除 k 即可。
由于前驱是小于根结点权值的最大的数,所以只要先进入左子树,然后一直向右找即可。
后继同理。
注意,下面代码返回的是结点编号,所以在最后输出的时候要套一层 val[]。
int get_pre() { // 查询根节点的前驱
int x = son[root][0]; // 进入左子树
while (son[x][1]) x = son[x][1]; // 一直往右找
splay(x, 0); // 旋转至根结点
return x;
}
int get_nxt() { // 查询根节点的后继
int x = son[root][1]; // 进入右子树
while (son[x][0]) x = son[x][0]; // 一直往左找
splay(x, 0); // 旋转至根结点
return x;
}
合并两颗 Splay 树
设两棵树的根结点分别为 x,y ,那么要求 x 树中的最大值小于 y 树中的最小值。
- 若 x=\varnothing 或 y=\varnothing ,那么返回非空的树或者空树。
- 否则将 x 树中最大值 splay 至根结点,然后将其右子树设为 y 。这样就保证了二叉搜索树的性质。
这只是一个辅助删除结点的思想,并不需要具体实现为一个函数。
删除一个结点
假设要删除一个权值为 k 的数。
如果要将权值为 k 的数,那么直接将计数器置为 0 即可。
首先将 x 旋转到根结点。
- 若
cnt[x] > 1,那么--cnt[x]并返回。 - 否则删除根结点,并合并左右子树。
思路听起来很简单,但是实现起来有一定的理解难度。
void erase(int k) { // 删除一个权值为 k 的数
get_rank(k); // 因为只知道权值为 k,那么可以用查找 k 的排名函数找到权值为 k 的结点并将其旋转至根结点
if (cnt[root] > 1) { // 直接删除一个数
--cnt[root];
pushup(root); // 更新大小
return ;
}
if (!son[root][0] && !son[root][1]) { // 树中只有一个根结点
clear(root); // 清空根结点
root = 0; // 根结点置为 0
return ;
}
if (!son[root][0]) { // 左子树为空
int cur = root;
root = son[root][1]; // 将根结点设为右子树的根结点
fa[root] = 0; // 将父亲设为空
clear(cur); // 清除原来的根结点
return ;
}
if (!son[root][1]) { // 右子树为空
int cur = root; // 将根结点设为左子树的根结点
fa[root = son[root][0]] = 0;
clear(cur);
return ;
}
/*
由于原树分裂成了左右子树,而左子树的最大值必然小于右子树的最小值,那么左子树为 x,右子树为 y。
x = get_pre() 得到了 x 中的最大值,并同时通过 splay 操作将其旋转至整棵树的根结点。
此时将原树的右儿子的父亲设为当前根结点,并且更新儿子关系。
最后清除原根节点,并且更新根结点大小。
*/
int cur = root, x = get_pre();
fa[son[cur][1]] = x;
son[x][1] = son[cur][1];
clear(cur);
pushup(root);
}
完整代码
其中 N 为最大的总共开的点的数量,如果不确定可以用 std::vector 代替。
struct Splay {
int root, tot, val[N], siz[N], cnt[N], fa[N], son[N][2];
void pushup(int x) { // 合并 x 的左儿子与右儿子,得到 x 的大小
siz[x] = siz[son[x][0]] + siz[son[x][1]] + cnt[x];
}
bool get(int x) { // get(x)=1 说明 x 是右儿子,反之是左儿子
return x == son[fa[x]][1];
}
void clear(int x) { // 销毁结点 x
son[x][0] = son[x][1] = fa[x] = val[x] = siz[x] = cnt[x] = 0;
}
void rotate(int x) {
int y = fa[x], z = fa[y];
int id = get(x); // 判断 x 是 y 的左儿子还是右儿子
if (z) son[z][get(y)] = x;
fa[x] = z;
son[y][id] = son[x][id ^ 1];
if (son[x][id ^ 1]) fa[son[x][id ^ 1]] = y;
son[x][id ^ 1] = y, fa[y] = x;
pushup(y), pushup(x);
}
void splay(int x, int k) { // 将 x 转到 k 的下面
while (fa[x] != k) {
int y = fa[x], z = fa[y];
if (z != k) {
if (get(x) ^ get(y)) rotate(x);
else rotate(y);
}
rotate(x);
}
if (!k) root = x;
}
void insert(int k) {
if (!root) { // 树为空
val[++tot] = k;
++cnt[tot];
root = tot;
pushup(root);
return ;
}
int x = root, y = 0;
while (true) {
if (val[x] == k) { // 找到目标
++cnt[x];
pushup(x), pushup(y);
splay(x, 0);
break;
}
y = x, x = son[x][val[x] < k];
if (!x) { // 插入新结点
val[++tot] = k;
++cnt[tot];
fa[tot] = y;
son[y][val[y] < k] = tot;
pushup(tot);
pushup(y);
splay(tot, 0);
break;
}
}
}
int get_rank(int k) { // 查询 k 的排名
int res = 0, x = root;
while (true) {
if (k < val[x]) x = son[x][0]; // k 落在 x 的左子树
else {
res += siz[son[x][0]];
if (!x) return res + 1;
if (val[x] == k) return splay(x, 0), res + 1;
res += cnt[x], x = son[x][1];
}
}
return -1;
}
int get_kth(int k) { // 查询排名为 k 的数
int x = root;
while (true) {
if (son[x][0] && k <= siz[son[x][0]]) x = son[x][0];
else {
k -= cnt[x] + siz[son[x][0]];
if (k <= 0) return splay(x, 0), val[x];
x = son[x][1];
}
}
return -1;
}
int get_pre() { // 查询根节点的前驱
int x = son[root][0];
while (son[x][1]) x = son[x][1];
splay(x, 0);
return x;
}
int get_nxt() { // 查询根节点的后继
int x = son[root][1];
while (son[x][0]) x = son[x][0];
splay(x, 0);
return x;
}
void erase(int k) { // 删除一个权值为 k 的数
get_rank(k);
if (cnt[root] > 1) {
--cnt[root];
pushup(root);
return ;
}
if (!son[root][0] && !son[root][1]) { // 树中只有一个根结点
clear(root);
root = 0;
return ;
}
if (!son[root][0]) { // 左子树为空
int cur = root;
root = son[root][1];
fa[root] = 0;
clear(cur);
return ;
}
if (!son[root][1]) { // 右子树为空
int cur = root;
fa[root = son[root][0]] = 0;
clear(cur);
return ;
}
int cur = root, x = get_pre();
fa[son[cur][1]] = x;
son[x][1] = son[cur][1];
clear(cur);
pushup(root);
}
} tree;