姓名: 施泽家
赛道: 基础组
类型: 算法及能
【算法一锅炖~~酸甜苦辣自己的选择】
**关键词:**基础算法、 排序、搜索、数和图
uint 1:
1 结构体
在C++中,你可以使用struct关键字来定义一个结构体。结构
体是一种用户自定义的数据类型,它可以包含不同类型的数据。
结构体的定义框架
struct 变量名
{
定义的数据类型(像int,double,float等等) 变量名;
...(其他内容省略)
};
定义结构体变量
变量名 变量(数组);
uint 2:
2 排序
排序有好多种:选择排序、冒泡排序、插入排序,桶排序,快速排序,归并排序,堆排序
但在此之前我们要先了解时间复杂度
时间复杂度通常是通过大O符号来表示的,它描述了算法执行时间随着输入大小增长的增长率。常见
的时间复杂度有O(1)(常数时间)、O(log n)(对数时间)、O(n)(线性时间)、O(n log n)(线性对
数时间)、O(n^2)(平方时间)、O(n^3)(立方时间)、O(2^n)(指数时间)、O(n!)(阶乘时间)等。
1.冒泡排序
思想:
冒泡排序是一种简单的排序算法,它重复地遍历要排序的数列,一次比较两个元素,如果它们的
顺序错误就把它们交换过来。重复进行直到没有再需要交换的元素,这意味着数列已经排序完成。
核心代码
// 输入
// 冒泡排序(从小到大)
for (int i = 1; i < n; i++)
{ // 一共有n-1轮(每一轮安排好一个数字)
for (int j = 0; j < n - i; j++)
{ // 循环数组的下标
if (a[j] > a[j + 1])
{
swap(a[j], a[j + 1]);
}
}
}
// 输出
2.选择排序
思想:
选择排序是一种简单直观的排序算法,其基本思路是在未排序的序
列中找到极端元素(最大或最小),然后将其存放到序列的起始位置
核心代码
// 输入
// 选择排序(从小到大)
for (int i = 0; i < n - 1; i++)
{ // 在位置i放一个最小值
int x = i;
// 找最小值的位置x
for(int j = x + 1; j < n; j++)
{
if (a[x]> a[j])
{
x = j;
}
}
swap(a[i], a[x]);
}
// 输出
3.插入排序
思想:
插入排序是一种简单直观的排序算法,其工作原理是通过构建有序序列,
对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
核心代码
// 输入
// 插入排序
for (int i = 1; i < n; i++)
{ // 要把a[i]插入到正确的位置
int x = a[i];
int j = i - 1;
for ( ; j >= 0; j--)
{ // 从后往前判断
if (a[j] > x)
{
a[j + 1] = a[j]; // 把数组往后挪
}
else
{
break;
}
}
// 把x放到当前的位置
a[j + 1] = x;
}
// 输出
4.桶排序
思路:
桶排序=是一种排序算法,工作原理是将数组分 into 几个桶,每个桶再分别排序,当所有桶都排好序后,再将所有桶中的数据按顺序输出。它是一种稳定的排序算法,适用于一些特殊的场合,如数据分布在一定范围内。
核心代码
//输出
for (int i = 0; i < n; i++) {
cin >> x;
a[x]++;
}
// 输出
5.快速排序
思路:
快速排序是一种高效的排序算法,它使用分治策略来对一个数组进行排序。
核心代码
int part(int* r, int low, int hight) //划分函数
{
int i = low, j = hight, pivot = r[low]; //基准元素
while (i < j)
{
while (i<j && r[j]>pivot) //从右向左开始找一个 小于等于 pivot的数值
{
j--;
}
if (i < j)
{
swap(r[i++], r[j]); //r[i]和r[j]交换后 i 向右移动一位
}
while (i < j && r[i] <= pivot) //从左向右开始找一个 大于 pivot的数值
{
i++;
}
if (i < j)
{
swap(r[i], r[j--]); //r[i]和r[j]交换后 i 向左移动一位
}
}
return i; //返回最终划分完成后基准元素所在的位置
}
6.归并排序
思路:
归并排序是一种稳定的排序算法,适用于对大规模数据的排序。
核心代码
void Merge(int a[], int left, int mid, int right){
int temp[right - left + 1]; //临时数组用于存储排序时的数
int i = left; //分成两块 i指向左边的数字 j指向右边的数字
int j = mid + 1;
int k = 0; //k用于存储数字到临时数组
while( i <= mid && j <= right ){
if(a[i] < a[j]) //永远都是 i 和 j 指向的数进行比较
temp[k++] = a[i++]; //谁小,谁就先放到临时数组中
else
temp[k++] = a[j++];
}
while( i <= mid ) //如果左边还有数没放上去,就依次放上去
temp[k++] = a[i++];
while( j <= right ) //如果是右边还有同上
temp[k++] = a[j++];
for(int m = left, n = 0; m <= right; m++, n++)//读取临时数组中的数
a[m] = temp[n];
}
void Merge_Sort(int a[], int left, int right){
if( left == right )
return;
int mid = (left + right)/2;
//递归拆分成较小规模子序列排序
Merge_Sort(a, left, mid);
Merge_Sort(a, mid + 1, right);
Merge(a, left, mid, right); //合并较小规模问题解
}
void Show(int a[], int n){
for(int i = 0; i < n; i++)
cout<<a[i]<<" ";
cout<<endl;
}
或者直接写 stable_sort();
7.堆排序
思路:
一个视频
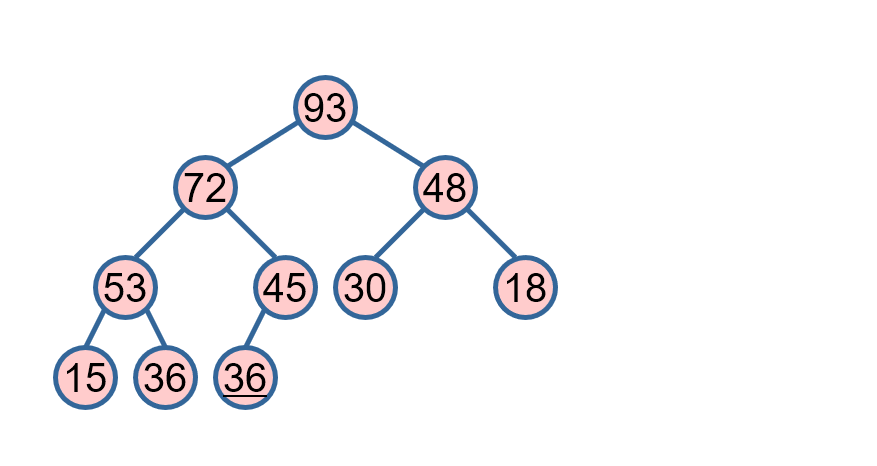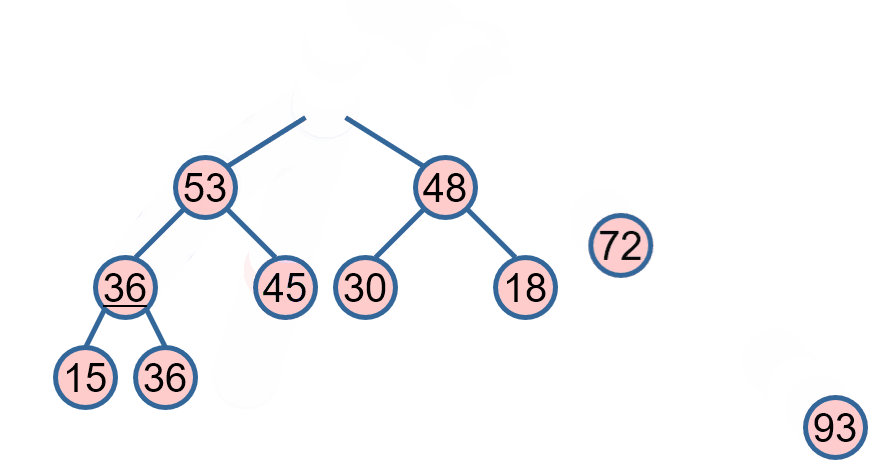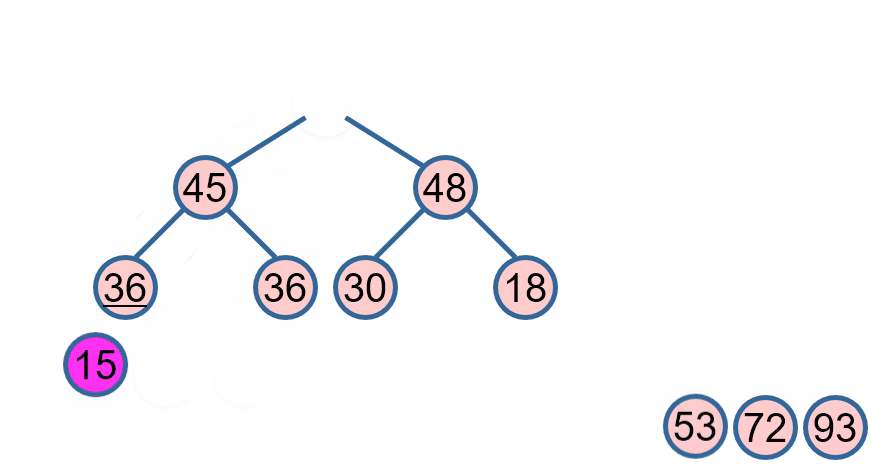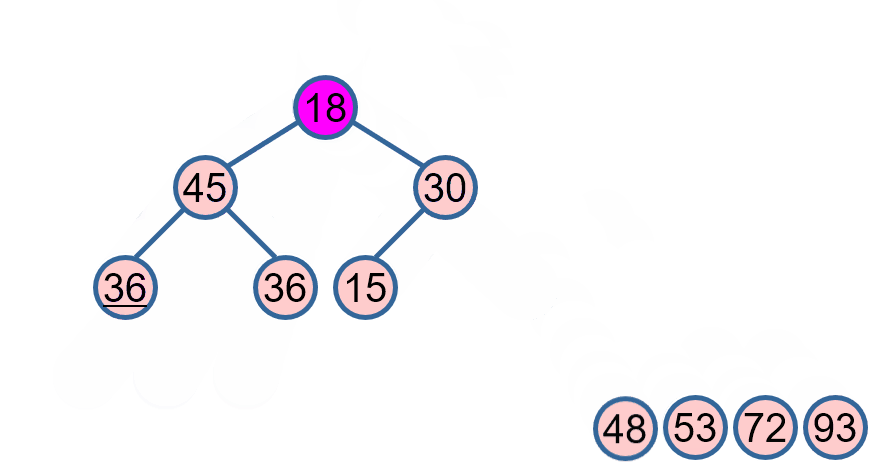
堆排序是一种基于比较的排序算法,它利用了二叉堆(一种特殊的完全二叉树)的性质来进行排序。在最大堆中,每个节点的值都不小于其子节点的值;在最小堆中,每个节点的值都不大于其子节点的值。
核心代码
void heapify(vector<int>& arr, int n, int i) {
int largest = i; // 初始化最大值为根节点
int left = 2 * i + 1; // 左子节点
int right = 2 * i + 2; // 右子节点
// 如果左子节点大于根节点
if (left < n && arr[left] > arr[largest])
largest = left;
// 如果右子节点大于目前的最大值
if (right < n && arr[right] > arr[largest])
largest = right;
// 如果最大值不是根节点
if (largest != i) {
swap(arr[i], arr[largest]); // 交换根节点和最大值节点
// 递归地对受影响的子树进行堆化
heapify(arr, n, largest);
}
}
// 堆排序的主函数
void heapSort(vector<int>& arr) {
int n = arr.size();
// 构建堆(重新排列数组)
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
// 逐个提取元素
for (int i = n - 1; i > 0; i--) {
// 将当前根节点移到末尾
swap(arr[0], arr[i]);
// 调用heapify在减少的堆上
heapify(arr, i, 0);
}
}
uint 3:
3 搜索
1.dfs
思路:
深度优先搜索(DFS)在C++中的实现主要依赖于递归和回溯的思想。
深度优先搜索(DFS)是一种用于遍历或搜索树或图的算法。这种算法会尽可能深地搜索树的分支。当节点v的边都已被探寻过,搜索将回溯到发现节点v的那条边的起始节点,这个过程一直进行到已发现从源节点可达的所有节点为止。如果在搜索过程中存在未被发现的节点,则选择其中一个作为新的源节点并重复以上过程,直到所有节点都被访问为止1。
在C++中实现DFS,通常涉及以下几个步骤:
- 选择起始节点:从图的某个节点开始,这个节点被称为源节点。
- 递归探索:从源节点开始,沿着一条路径尽可能深入图的分支。当到达一个终点或无法继续前进时,回溯到上一个节点,继续探索其他路径。
- 标记访问状态:使用一个数据结构(如数组或集合)来跟踪已经访问过的节点,以避免重复访问。
- 回溯:当当前节点的所有未访问的邻居节点都被探索过后,回溯到上一个节点,继续探索其他路径。
在C++中,DFS的实现可以通过递归函数来完成。递归函数会检查当前节点的所有未访问的邻居节点,并对每个未访问的邻居节点递归调用DFS函数。当所有可达的节点都被访问后,递归调用栈会自然回溯,从而实现深度优先搜索12。
此外,DFS的实现还需要考虑如何处理边界条件,例如当所有可达节点都被访问后如何停止搜索,以及如何处理无法到达的死胡同情况。
例题
1. 抽奖
题目描述:
在一个不透明的盒子里放入编号为 1~n 的 n 个球,每次只能摸一个球,然后把这个球放回盒子里摇匀后再摸,现在你可以抽取 n 次,请输出所有可能出现的结果。
数据格式:
输入一个整数(范围1到9),表示 n 个小球,抽取 n 次。
按字典序从小到大的顺序输出若干行可能出现的结果。
样例输入:
2
样例输出:
1 1
1 2
2 1
2 2
这道题就是求2的排列,一一遍历即可。
#include<bits/stdc++.h>
using namespace std;
int n;
int a[1005];
bool b[1005];
void dfs(int s)
{
if(s>n)
{
for(i,1,n)
{
//输出a[i]+空格
}
//换行
//返回
}
else
{
for(i,1,n)
{
//标记b[i]
//赋值a[s]为i
//释放b[i]
dfs(s+1);
}
}
}
int main()
{
//输入
dfs(1);
return 0;
}
接下来加亿点点难度 ![]()
2. 迷宫最小步数-弱化版
题目描述
给定一个大小为n * m的迷宫,求出从起点到终点的最小步数 ,只能上下左右四个方向走(若起点无法到达终点则输出-1)【*代表通道、#代表墙壁】
输入格式
第一行,两个整数n,m
第2~n+1行,每行输入一个长度为m的字符串(由*和#组成)
第n+2行,4个整数a,b,c,d 代表起点(a,b),终点(c,d)
输出格式
一个整数,代表从起点到终点的最小步数。
样例
Input 1
5 6
*****#
*##*##
*#**##
*#*#*#
******
1 1 5 3
Output 1
6
数据范围
0<n,m<50
cin>> ;//输入n和m;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>> ;//创建地图
}
}
cin>> ; //输入起始坐标和终点坐标
因为题目让我们输出最小值,所以我们的ans就要为最大值,而int中的最大值就是 0x3f3f3f,INT_MAX的意思是把一个数组中的数值初始化成正无穷大,这时就需要用INT_MAX代替,避免溢出。 如果dfs结束时ans还为INT_MAX,那么说明dfs中没有找到这个数,那么我们就要输出**-1**,否则就说明找到了,那么我们就要输出ans。
int ans= ;/*将ans定位int的最大值*/
if(/*如果ans不变*/)
{
cout<<-1;
}
else ;//输出最小值
接下来就轮到了重中之重,dfs了
首先我们得了解dfs的基础是递归,而递归必定有结束条件,不然就会进入死循环(结束条件的描述有很多种,可以单独判断,有时也可以和循环的循环条件融为一体),所以,我们首要知道这个dfs的结束条件是什么。
如果当前步数超过了上一次的步数,就说明它不是最短路径,就直接return掉
或者是到达了终点,那也直接renturn掉
因此我们就可以写出结束条件了
if(/*如果当前步数超过了上一次的步数*/) return ;
if(/*到达了终点(当前x坐标等于终点的x坐标,当前的y坐标等于终点的y坐标)*/)
{
//将现在的ans与cnt比较,得出较小值
return ;
}
然后,我们通过题面所说的只能上下左右四个方向走一话,我们就可以模拟出所有的情况
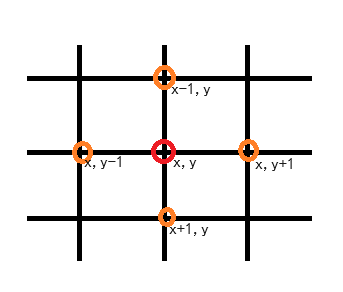
现在我们已经找到了4种情况我们就可以把这几种情况列出来
int dx[]={-1,0,1,0};
int dy[]={0,1,0,-1};
当4种情况都列出来后,我们就可以逐个遍历,当然是用for循环了
因为是4种情况,而且我们的数组定义的也是从零开始的,所以
for(int i=0 ;i<4;i++)
{
}
然后我们思考,for循环中写什么呢?
因为每一次我们的x和y都是在运动着的,所以我们可以设两个下一步的x(ex)和y(ey)。
这时,我们就可以计算,这时的新x和y,就等于原本的x和y加上现在走的一步的方向,这样我们就可以递归了。
int ex=x+dx[i];
int ey=y+dy[i];
这时我们就要考虑最开始时很多问题了。
1 怎么处理边界
我们可以判断此时的x(ex)和y(ey)是否处于边界之内
2 是否是障碍物
3 是否走过
if(ex<1||ex>n||ey<1||ey>m||mp[ex][ey]=='#'||vis[ex][ey]==1)
如果满足其一,就continue
否则就说明当前位置可以走,那么就把当前位置设为1,然后dfs调用,因为题目中是有多种走到终点的可能性,所以我们要回溯,将vis设为0
else
{
//把当前位置设为走过
dfs(ex,ey,cnt+1);
//回溯
}
是不是特别简单
2.bfs
十四、bfs
广度(宽度)优先算法的核心思想是:使用队列(queue)从初始节点开始,应用算符生成第一层节点,检查目标节点是否在这些后继节点中,若没有,再用产生式规则将所有第一层的节点逐一扩展,得到第二层节点,并逐一检查第二层节点中是否包含目标节点。
例题
- 好马不吃回头草
题目描述
“好马不吃回头草!”。有道理!!!,虽然鱼大大也不知道道理在哪里,但是他就是觉得这句话很有道理。于是乎,他便养成了一个习惯,下象棋时,他的马从来都是毫无撤退可言!
现给出一张巨大的棋盘,问象棋中的马(走日字型,由鱼大大操控),从棋盘上一个点吃掉另一个点的“帅”最少需要几步。(起点记作0步,帅不动) 注: 鱼大大在黑色方,即上方,每次只能往下方走。
输入格式
第一行输入一个整数n,表示棋盘的大小为 n*n,棋盘两个维度的坐标都是从 1 到 n。
接下来两行每行两个整数分别表示马出发点的坐标与帅终点的坐标。(第一个为行,第二个为列)
输出格式
输出一个整数,表示最小步数,若无法到达输出 -1。
样例输入
50 1 1 30 50
样例输出
26
数据范围
3 ≤ n ≤ 500;
这道题的关键 要看清楚题目,只往下走,不往上走,所以dx和dy只有四项
核心代码
void bfs(int x,int y)
{
queue<Node> qu;
qu.push({x,y,0});
b[x][y]=1;
while(!qu.empty())
{
Node now=qu.front();
qu.pop();
if(now.x==enx&&now.y==eny)
{
//输出now.cnt
//回溯
}
for(int i=0;i<4;i++)
{
int nx=now.x+dx[i];
int ny=now.y+dy[i];
int ncnt=now.cnt+1;
if(nx<1||ny<1||nx>n||ny>n||b[nx][ny]==1) continue;
b[nx][ny]=1;
qu.push({nx,ny,ncnt});
}
}
//输出-1
}
接着来讲最后一个知识点 ~数和图~
结点的度:结点拥有的子树个数或者分支的个数。如A结点有三棵子树、所以A结点的度为3
树的度:树中各结点度的最大值。如图中结点度最大为3(A、D结点),所以树的度为3。
树的深度(或高度):树中结点的最大层次。
树的宽度:整棵树中某一层中最多的结点数称为树的宽度。
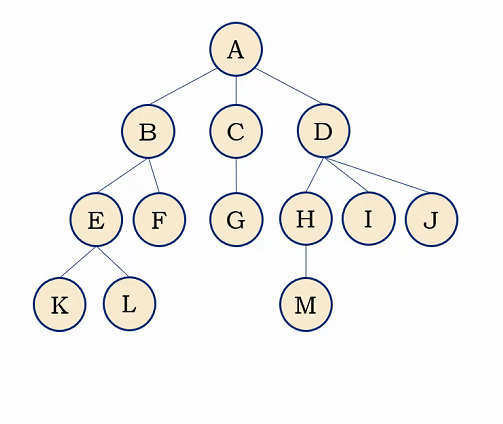
根结点:一棵树至少有一个结点,这个结点就是根结点
叶子结点:又叫做终端结点,指度为0的结点。
非终端结点:又叫分支结点,指度不为0的结点,都是非终端结点。除了根结点之外的非终端结点,也叫做内部结点。
父结点/双亲结点:称上端结点为下端结点的父结点。
孩子结点:称下端结点为上端结点的子结点。
兄弟结点:称同一个父结点的多个子结点为兄弟结点。
祖先节点:又称从根节点到某个子结点所经过的所有结点称为这个结点的祖先。
子孙结点:称以某个结点为根的子树的任一结点都是该节点的子孙
当然我们还是要会写代码的
树的宽度
void dfs(int x,int deep){
mm[deep]++;
max_deep=max(max_deep,mm[deep]);
for(int i=1;i<=n;i++){
if(a[x][i]=='1'&&vis[i]==0){
vis[i]=1;
dfs(i,deep+1);
}
}
}
树的深度
void dfs(int x,int deep){
max_deep=max(max_deep,deep);
for(int i=1;i<=n;i++){
if(a[x][i]=='1'&&vis[i]==0){
vis[i]=1;
dfs(i,deep+1);
}
}
}
剩余的就非常简单了~
点个赞吧

