姓名: 俞天行
赛道: 普及组
类型: 算法技能
二进制与二叉树:一场数学与编程的交响乐
关键词: 二进制、二叉树、数据结构
一、引言
一场数学与编程的交响乐
上篇:二叉树
- 树根立高天,无数支划分开。
层层递进枝叶茂,深度四时满树栽。
一层节点数倍增,
双子相承相辅随。
零至十五节点共,
归根结底数理知。
中篇:二进制
- 数码间千变万化,
四位引得十进制。
零一之间道真谛,
内蕴逻辑无尽魅。
四位足以数一切,
最上极限十与二。
从零到十五任意取,
简明扼要尽自然。
下篇:比较共鸣
- 树形与数均相映,
信息承载各自奇。
一构复杂生巧妙,
一显简易藏深思。
编程之奥求真理,
数学之美诉情怀。
二叉数与二进制,
彼此辉映共成长。
尾声
- 探寻数的无穷境,
逻辑与结构相拥辉。
在这知识的殿堂里,
任思维如风自由飞。
二进制
- 二进制是计算技术中广泛采用的一种数制 。二进制数据是用0和1两个数码来表示的数。它的基数为2,进位规则是逢二进一 。
二叉树
- 二叉树是一种一对多的树型结构 ,除空二叉树外,有一个唯一的根接点,左、右子树都是二叉树。
在编程与数据结构的领域中,它们虽然名字里都有二,但各自占据着重要的位置。在概念上似乎没有很多交集,那如果他们碰撞在一起又会擦出怎样的火花——
二、基本介绍
在对比他们之前,我们先简单了解一下关于他们的知识 (此部分干货过多,请谨慎观看)
二进制
1.关于进制
在学习进制之前,我们要弄清一点,何为进制?
进制:
是一种计数的方法,是用一组固定的符号和统一的规则来表示数值的方法。包括数位、基数和位权三个要素。
-
数位:指数字符号在一个数中所处的位置。
拿int类型最大数字2147483647举例:
2 1 4 7 4 8 3 6 4 7 十亿 亿位 千万 百万 十万 万位 千位 百位 十位 个位 -
基数:指在某种进位计数制中数位上所能使用的数字符号的个数。例如十进制的基数为10
-
位权:数制中某一位上的1所表示数值的大小(所处位置的价值)。例如十进制的230,1的位权是100,2的位权是10,3的位权是1
那么除了十进制,计算机还有哪些常用的进制,怎么表示呢?
天空一声巨响,进制家族闪亮登场 ![]()
\color{blue}{二进制} :
- 逢二进一,每位数字 \in 0,1
\color{blue}{八进制} :
- 逢八进一,每位数字 \in 0,1,2,3,4,5,6,7
\color{blue}{十六进制} :
- 逢十六进一,每位数字——没有比9大的怎么办???
凉拌,用大写字母A~F表示,
所以每位数字 \in 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F ,
-
PS:如果你想自己创造进制
那么,如果进制为 n ,
那么 n 进制的数字(下文用x表示)每一位应该 0 ≤ x ≤ n - 1
但是除了一些显著的特征之外(如16进制可能有A~F),我们如何区分一个数字是几进制呢?
1011
上面这个数只有0与1组成,那么到底是几进制的?
1)在数字后加上该数值的英文字母
| 进制 | 表示字母 |
|---|---|
| 二进制 | B(binary) |
| 八进制 | O(octal) |
| 十进制 | D(decimal) |
| 十六进制 | H(hexadecimal) |
2)数值+进制
前面这两种是数学的表示方式,既然我们是学计算机的,那自然有第三种表示方法
3)属于我们计算机界的独特方法
数字:36 (我的学号)
| 进制 | 表示方法 |
|---|---|
| 二进制 | 0b 100100 或 0B 100100 |
| 八进制 | 0 44 |
| 十进制 | 36 |
| 十六进制 | 0x 24 或 0X 24 |
2.进制转换
既然弄明白了进制,那不同进制之间怎么转换呢?
- n进制转十进制
还记得位权吗?






那好,举个栗子
| 数 : | 5 | 4 | 7 | 3 | 8 | . | 2 | 8 | 3 | 7 |
|---|---|---|---|---|---|---|---|---|---|---|
| 位权 : | 10000 | 1000 | 100 | 10 | 1 | . | 0.1 | 0.01 | 0.001 | 0.0001 |
| 10^4 | 10^3 | 10^2 | 10^1 | 10^0 | . | 10^- ^1 | 10^- ^2 | 10^- ^3 | 10^- ^4 |
懂?
- 懂啦(^▽^)
- 废啦o((⊙﹏⊙))o

那么到底如何转换呢?
- 0b1011.11 → 十进制
0b1011.11
= b_4(1) \times 2^3 + b_{3}(0) \times 2^{3} + b_2(1) \times 2^1 + b_1(1) \times 2^0 + b_{-1}(1)
\times 2^{-1} + b_{-2}(1) \times 2^{-2}
=10.75
\color{red}{SO} You will be like them. Will you?
我们可以得出结论(进制为 k ,每位为 n ~ 1)
b = b_n \times 2^{k-1} + b_{n-1} \times 2^{k-2} + \ldots + b_2 \times 2^1 + b_1 \times 2^0
- 十进制转n进制(整数)
- 13D = ? B
要解决这个问题,首先,我们得知道一个好东东:短除法
我想你们都知道,不会请上百度自行学习
用法如下(拿13转二进制为例)
2 |_ 13__
2 |_ 6__ ……1 ↑ 从
2 |_ 3__ ……0 ↑ 下
2 |_ 1__ ……1 ↑ 往
2 |_ 0__ ……1 ↑ 上
一个数用短除法除以要转换的进制,一直除到结果为0,再把余数从下往上念
所以
- 13D = 1011B
简单吧?






对了,顺便说一句,如果要将 二进制 → 八进制 或 十六进制 ,那么你运气爆棚了,不需要先转换成十进制,因为3位二进制表示1位八进制(八进制最大的7用二进制表示为111),4位二进制表示1十六进制(十六进制最大的15用二进制表示为1111)。
- 十进制转n进制(小数)
是不是很简单?来看看下面这组数字:
0.56D = \color{red}{?B}
0.56 \times 2 = 1.12 ——取出整数部位1
0.12 \times 2 = 0.24 ——取出整数部位0
0.24 \times 2 = 0.48 ——取出整数部位0
0.48 \times 2 = 0.96 ——取出整数部位0
0.96 \times 2 = 1.92 ——取出整数部位1
0.92 \times 2 = 1.84 ——取出整数部位1
0.84 \times 2 = 1.78 ——取出整数部位1
0.78 \times 2 = 1.56 ——取出整数部位1
提取到这以后,突然发现:咦,怎么又回开头了?
其实这个数在二进制是个循环小数,惊喜吧? ![]()
3.计算机的编码方式
计算机中的数值编码方式主要包括原码、反码和补码。这三种编码方式十分重要,因为它们影响计算机如何表示和处理整数,尤其是有符号整数。
- 原码
定义:
原码是表示整数的一种方式,它使用最高位符号位来指示数的符号,0表示正数,1表示负数,其余位表示数值的大小。
表示方法:
- 正数的原码:符号位为0,后续位表示数值。例如,+5在8位二进制中表示为
00000101。 - 负数的原码:符号位为1,后续位表示数值的绝对值。例如,-5在8位二进制中表示为
10000101。
工作原理: 由于原码的表示方式,进行运算(如加法)时需要判断符号并进行相应的处理。在实际应用中,原码会导致一些运算问题,比如同一数值有两种形式(+0和-0)。
- 反码
定义: 反码是原码的一种变体,用于表示整数。它的符号位保持不变,数值部分通过对原码的每一位取反而得到。
表示方法:
- 正数的反码:与原码相同,例如,+5的反码是
00000101。 - 负数的反码:对正数的原码取反,符号位仍然是1。例如,-5的原码是
10000101,取反后变成11111010。
工作原理: 反码的加法运算需要处理进位的问题。对于负数,进行相加时加上一个进位表示0,结果为0(即11111111表示-0,与正0重复出现的问题)。
- 补码
定义: 补码是现代计算机中最常用的有符号整数表示方式。它通过对反码加1的方式来得到。
表示方法:
- 正数的补码:与原码和反码相同。例如,+5的补码是
00000101。 - 负数的补码:首先求其原码,然后取反再加1。例如,-5的原码是
10000101,其反码是11111010,加1后为11111011。
工作原理:
补码的优点在于:
- 加法和减法可以统一处理,无需分开考虑符号位。
- 仅有一种零的表示形式,减少计算中的异常情况。
- 直接使用现有的加法器电路就可以进行减法运算(减法可以转换为加上数的补码)。
总结
- 原码的表示方式简单,但由于存在两个零(+0和-0),处理运算时极易出错。
- 反码改善了原码的问题,但依然存在两个零的问题,使得其在实际应用中并不广泛。
- 补码克服了前两者的问题,成为现代计算机中主流的整数表示方式,效率高而且处理方便。
通过补码的使用,计算机能够简化有符号数字的运算,同时提高运算效率。
位运算
讲二进制,那肯定要讲位运算
位运算是计算机科学中一种直接对二进制数的各个比特位进行操作的运算。在许多底层编程和算法中,位运算可以提高效率和性能。位运算包括按位与(AND)、按位或(OR)、按位异或(XOR)、按位取反(NOT)和位移操作等。以下是每种位运算的详细说明以及它们的优先级。
- 按位与(AND)运算
运算符:& 或 ∧
定义: 按位与运算对两个数的每一位上的比特进行比较,只有在两个对应的比特都是1时,该位结果才为1;否则结果为0。
真值表:
| A | B | A ∧ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
数学示例:
1010 (十进制10)
& 1100 (十进制12)
--------
1000 (十进制8)
- 按位或(OR)运算
运算符:| 或 ∨
定义: 按位或运算对两个数的每一位上的比特进行比较,只要有一个比特为1,则该位结果为1;如果两个比特均为0,结果为0。
真值表:
| A | B | A ∨ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
数学示例:
1010 (十进制10)
| 1100 (十进制12)
--------
1110 (十进制14)
- 按位异或(XOR)运算
运算符:^ 或 ⊕
定义: 按位异或运算对两个数的每一位上的比特进行比较,当两个比特不相同时,该位结果为1;当两个比特相同时,结果为0。
真值表:
| A | B | A ⊕ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
数学示例:
1010 (十进制10)
^ 1100 (十进制12)
--------
0110 (十进制6)
- 按位取反(NOT)运算
运算符:~ 或 ¬
定义: 按位取反运算对一个数的每一位进行取反操作,即1变为0,0变为1。
数学示例:
~ 1010 (十进制10)
--------
0101 (十进制5,补码表示下为-11)
注意,取反后可能会由于补码表示的性质导致负数。
- 左移(Left Shift)运算
运算符:<<
定义: 左移运算符将一个数的所有比特向左移动指定的位数,右侧用0填充。左移相当于将数字乘以2的幂。
数学示例:
00000010 (十进制2)
<< 2
---------
00001000 (十进制8)
- 右移(Right Shift)运算
运算符:>>
定义: 右移运算符将一个数的所有比特向右移动指定的位数。对于无符号数,左侧用0填充;对于有符号数,某些编译器使用算术右移(保持符号位不变),另一些则执行逻辑右移(无论正负,都用0填充)。
数学示例:
00001000 (十进制8)
>> 2
---------
00000010 (十进制2)
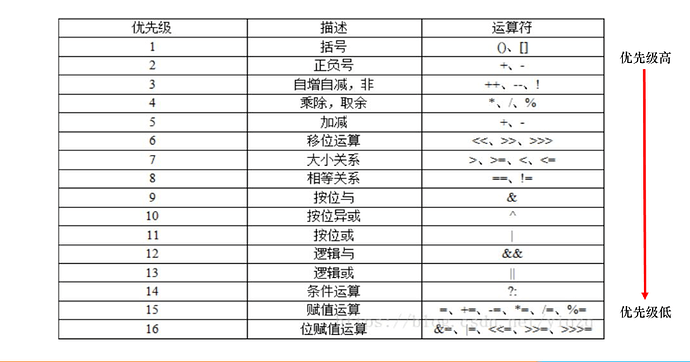
运算优先级
在C++中,位运算是有优先级的,不然就没有顺序了,优先级如下(从高到低):
在进行复杂的位运算时,推荐使用括号来明确运算顺序,避免优先级导致的错误。比如:
int sum = a & (b | c); // 可以明确先计算b | c,然后再与a进行AND运算
总结
位运算是计算机基础当中一项重要的技能,理解每种位运算的工作原理和相互之间的优先级对进行高效的编程至关重要。同时,位运算通常用于优化算法,特别是在需要处理大量数据或进行低层次操作(如图像处理、网络通信等)的场景中。
上面就是二进制的一点点介绍,记下来,后面要考的 
—————————————————————————————————————————————
二叉树
数据结构
数据结构是什么 @苍穹一粟
数据结构是计算机科学中的一个基本概念,是特定的存储格式,用于组织、管理和存取数据。常见的数据结构有数组、链表、栈、队列、树、图等。
二叉树介绍
二叉树是一种特殊的树形数据结构,每个节点最多可以有两个子节点,这是二叉树的主要特征。二叉树的特性使得它在计算机科学中的很多领域(如表达式树、搜索树、堆等)都有广泛的应用。
1. What is 二叉树
二叉树是一种数据结构,是每个节点最多只能有两个子节点的树形结构。
先了解一些东西
- \text{leaf}(T) :表示树 T 的叶子节点的集合。
- \text{size}(T) :表示树 T 中节点的总数。
- \text{balance}(T) :表示树 T 的平衡因子,通常定义为左子树高度减去右子树高度,表达为 balance(X) = height(X.L) - height(X.R) 。
二叉树的基本概念如下:
- 节点
节点是二叉树的基本组成单元,每个节点包含三个部分:
- 数据域:存储节点的数据(如数字、字符等)。
- 左子节点指针:指向该节点的左子节点(可以是空)。
- 右子节点指针:指向该节点的右子节点(可以是空)。
表示方法
- 节点:通常用字母 如 A, B, C, … 或其他符号表示。
- 子节点:对于节点 X,左子节点用 X.L 表示,右子节点用 X.R 表示。
- 父节点:用 P.X 表示节点 X 的父节点,表示为 X.P 或 X 的父节点。
- 特性
- 每个节点最多有两个子节点,称为左子节点和右子节点。
- 二叉树的高度是从根节点到最深叶子节点的最长路径的边数。
- 种类
- 满二叉树:每个节点都有0或2个子节点的二叉树。
- 完全二叉树:除了最后一层外,其余层的节点都满了,并且最后一层的节点都集中在最左边。
- 二叉搜索树(BST):对于每个节点,所有右子树节点的值都大于该节点,所有左子树节点的值都小于该节点。
- 平衡二叉树:任何节点的两个子树的高度差的绝对值不超过1。
- 遍历
二叉树的遍历是访问树中每个节点的过程。主要有三种遍历方式:
- 前序遍历(Pre-order):访问根节点,遍历左子树,遍历右子树。根 → 左 → 右,表示为 PLR。
- 中序遍历(In-order):遍历左子树,访问根节点,遍历右子树。左 → 根 → 右,表示为 LPR。
- 后序遍历(Post-order):遍历左子树,遍历右子树,访问根节点。左 → 右 → 根,表示为 LRP。
- 层序遍历(Level-order):逐层从上到下访问节点,通常不使用特定的符号表示,但可以用队列来实现。
- 应用
- 二叉树广泛应用于数据处理、计算机科学中的各种算法(如排序、查找)、表达式解析、代表家谱结构等领域。
- 例子
假设有一个简单的二叉树如下:
A
/ \
B C
/ \
D E
- 这个二叉树的根节点是A,A的左子节点是B,右子节点是C。
- B的左子节点是D,右子节点是E。
- 叶子节点是D、E和C(没有子节点的节点)。
前序遍历:
ABDEC
中序遍历:
DBEAC
后序遍历:
DEBCA
2. 二叉树的性质
我们将讨论的重要性质如下:
- 在二叉树的第k层上最多有 2^{(k-1)} 个节点 k ≥ 1
在二叉树中,假设从根节点开始,根节点是第1层。根据层的定义,第k层的节点数一般是上一层节点数的两倍。换句话说:
- 第1层:1个节点(根节点)
- 第2层:最多2个节点
- 第3层:最多4个节点
- 第k层:最多 2^{(k-1)} 个节点 这就是该性质的推导。
- 深度为k的二叉树至多有 2^k - 1 个节点 k ≥ 1
深度k的二叉树是指从根节点到最深的叶子节点的最长路径为k。如果树是完全的,那么在每个层都达到了其最大节点数。因此,总节点数为: 1 + 2 + 4 + … + 2^{(k-1)} = 2^k - 1 这是一个等比数列求和公式的应用。 ← (记住他,第三部分论证的开始) - 对任何一棵二叉树,如果其终端节点数为 n_0 ,度为2的节点数为 n_2 ,则 n_0 = n_2 + 1
这里的“终端节点”是指没有子节点的节点,“度为2的节点”则是指有两个子节点的节点。我们可以通过数学证明这一性质:
-
证明:
- 设二叉树有 n_0 个终端节点, n_1 个度为1的节点, n_2 个度为2的节点。
- 每个节点在二叉树中要么是终端节点,要么至少会影响一个终端节点(即通过它的子节点)。
- 树的总边数也可以用子节点的数量来计算,由于每个节点相连接的边数与其子节点数有关:
- \because 度为2的节点贡献了2条边,度为1的节点贡献了1条边,终端节点不贡献边。
- \therefore 我们可以得到: n_2 + n_1 = n_0 + 1 根据节点的度数,我们可以进一步得到: 2n_2 + n_1 = n_0 + 1 将前面的公式代入,即得: 2n_2 + n_0 - n_2 = n_0 + 1 整理后得到: n_0 = n_2 + 1
- 具有n个节点的完全二叉树的深度为 |\log_2(n) + 1|
完全二叉树的定义是每层节点都达到最大值,只有最后一层节点可能不满。对于一个完全二叉树:
- 如果完全二叉树的深度为d,那么它的节点总数最大为 2^d - 1 。由于完全二叉树的节点数包含最后一层的不完整,实际节点数 (n) 满足: 2^{d-1} \leq n < 2^d 因此,我们可以得到: d = \lfloor \log_2(n) \rfloor + 1 而此深度通过上述公式验证成立。
3.特殊类型的二叉树
- 满二叉树(Full Binary Tree)
定义
满二叉树是每个节点都有0或2个子节点的二叉树。在满二叉树中,所有的叶子节点都位于同一层。
特性
- 如果树的高度为 h ,则满二叉树的节点总数 n 被计算为: n = 2^{h+1} - 1
- 在满二叉树中,叶子节点的数量是 2^h (高度为 h 的层)。
- 满二叉树的每个非叶子节点都有左子节点和右子节点。
示例
A
/ \
B C
/ \ / \
D E F G
- 完全二叉树(Complete Binary Tree)
定义
完全二叉树是一种特特殊的二叉树,其特点是除了最底层外,其余每一层的节点数都达到最大,并且最底层的节点都集中在左侧。
特性
- 如果树的高度为 h 且有 n 个节点,完全二叉树的节点总数可以是不完全的,但从根到第 h - 1 层都是满的,而第 h 层的节点应该尽量靠左排列。
- 完全二叉树的高度大约为 \log_2(n) 。
- 每一个节点 (i) 的父节点的索引为 \lfloor \frac{i-1}{2} \rfloor ,左子节点的索引为 2i + 1 ,右子节点的索引为 2i + 2 (假设从0开始索引)。
示例
A
/ \
B C
/ \ /
D E F
- 二叉搜索树(Binary Search Tree, BST)
定义
二叉搜索树是一种特殊的二叉树,具有如下性质:
- 对于树中的任意节点,左子树中所有节点的值都小于该节点的值,而右子树中所有节点的值都大于该节点的值。
特性
- 在二叉搜索树中,查找、插入和删除的平均时间复杂度为 O(\log n) ,但在最坏情况下(如形成了链状结构),时间复杂度为 O(n) 。
- 每个节点的键值是唯一的,不能重复。
- 中序遍历一棵二叉搜索树将产生一个递增的有序序列。
示例
D
/ \
B F
/ \ / \
A C E G
- 总结
- 满二叉树和完全二叉树主要在于它们的结构特征,均要求每层节点的填充状态;
- 二叉搜索树则通过特定的节点排序规则来增强对数据的快速检索能力;
- 这些特殊类型的二叉树在数据存储、检索、排序以及很多算法设计中都起着重要的作用。掌握它们的特性对于理解数据结构和算法的基本概念至关重要。
总之,二叉树具有方便的结构,使得在多种场景中能够有效得以管理和存取数据。
三、二进制与二叉树的联系
1. 二进制表示
二叉树中的每个节点最多有两个子节点,这一性质与二进制数的每一位只可能为0或1不谋而合。在某些情况下,二进制数可以被用来表示二叉树的结构。例如,一个满二叉树的第 (i) 个节点(从1开始计数)可以通过其在二进制下的表示来定位。根据完整二叉树的性质,第 (i) 个节点的位置可以表示为:
p(i) = \lfloor i/2 \rfloor, \quad \text{(父节点索引)}
l(i) = 2i, \quad r(i) = 2i + 1 \quad \text{(左、右子节点索引)}
2. 信息存储
无论是二进制数还是二叉树,它们都被广泛用于信息的存储与处理。在二进制编码中,每一位的0或1代表不同的信息,而在二叉树中,每个节点及其子节点组合也承载着特定的结构或数据信息。对于二进制数 b ,其表示为:
但是, \color{green}{上面的都还不是最重要的} ,重点 来了↓
3. 结构与应用
二叉树是一种树形数据结构,广泛应用于搜索、排序、表达式解析等算法中;而二进制是一种数值系统,是计算机内部信息表示的基础。二叉树的结构复杂,可以是不平衡的,树的高度 (h) 与节点数 (n) 的关系如下:
2^h - 1 \leq n < 2^{h+1} - 1
\color{red}{for} \color{red}{example} ,
对于深度为 h = 4 的二叉树,
n_{\text{max}} = 2^4 - 1 = 15
这里最大节点数为15。而将其与二进制数联系起来,我们可以注意到二进制数15的表示为:
15_{10} = 1111_2
这种对应关系表明,深度为4的二叉树能最多容纳15个节点,且用4位二进制数完全可以表示这种情况。
那么如何证明深度为4的二叉树能最多容纳15个节点?
我们首先定义什么是二叉树的深度。二叉树的深度(或高度)是从根节点到最远叶子节点的最长路径上的边的数量。深度从0开始计数,即根节点的深度为0,根节点的子节点的深度为1,以此类推。
最多节点数的推导:
- 深度为0的二叉树(只有根节点):最多有 2^0 = 1 个节点。
- 深度为1的二叉树:最多有 2^1 = 2 个子节点,总节点数为 1 + 2 = 3 。
- 深度为2的二叉树:最多有 2^2 = 4 个子节点,总节点数为 1 + 2 + 4 = 7 。
- 深度为3的二叉树:最多有 2^3 = 8 个子节点,总节点数为 1 + 2 + 4 + 8 = 15 。
- 深度为4的二叉树:最多有 2^4 = 16 个子节点,总节点数为 1 + 2 + 4 + 8 + 16 = 31 。
更一般地,当一棵二叉树的深度为 (h) 时,能容纳的最大节点数 n_{\text{max}} 为:
n_{\text{max}} = 2^{h+1} - 1
因此,当 (h = 4) 时:
n_{\text{max}} = 2^{4+1} - 1 = 2^5 - 1 = 32 - 1 = 31 \quad \text{(全体节点)}
但是,深度为4的完全二叉树,可以在此深度下只考虑完全填满的节点量,即最多填满每一层的节点,这样仍能容纳最多15个节点,分别在深度0到3填满,只在深度4留出一个(undefined)节点。
具体情况:
\text{深度为4的满二叉树最多叶子节点数} = 2^2 = 4 \quad \text{(深度为3时)}
再加上完全树形成层:
\text{深度4的二叉树最大节点数} = 1 + 2 + 4 + 8 = 15
所以,深度为4的二叉树最多能容纳15个节点。
在二进制系统中,4位二进制数的取值范围为:
0000_2 \text{ 到 } 1111_2
这意味着,有 2^4 = 16 种不同的组合。因此,4位二进制数能够表示从0到15的整数,正好涵盖了0到15这16个值。
节点索引问题:
我们通常通过从1到最多节点数来对节点进行编号,例如,如果我们希望表示一棵最大可容纳15个节点的二叉树,最简单的方式是使用一位二进制数:
- 最大节点的索引为15(编号为1至15)。
- 二进制表示如下所示:
| 节点编号 | 二进制表示 |
|---|---|
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
| …… | …… |
因此,我们可以看到,所有节点的编号(从1到15)都可以用二进制数进行表示(即0001到1111),这正好利用了4位的二进制数的全部可能性。
如果你还是不信邪,非要自己亲自尝试的话,加油吧ヾ(◍°∇°◍)ノ゙。
试到2147483647你就相信了 ![]()
用4位二进制数完全可以表示这种情况!
结论:
综上所述,我们证明了深度为4的二叉树最多能容纳15个节点,并且所有这些节点可以通过4位二进制数进行表示。这样形成了二叉树节点的索引与二进制数之间的直接映射关系。
三、总结
二叉树与二进制,虽同根但不同枝,各自在数据结构与数值系统领域中发挥着独特的作用。通过深入探讨它们之间的异同,以及数学反推与反演技巧的应用,我们不仅能够更加深刻地理解这些概念,还能在实际编程与问题解决中,构建更加高效的数学模型,实现算法的优化与创新。
在计算机科学的交响乐中,这两种结构交织在一起,共同谱写出一曲曲优雅而高效的数据处理与计算的乐章。通过深入的数学分析与编程实现,我们将继续推动这一领域的创新与发展。