姓名: 俞皓天(蛋小黄)
赛道: 普及组
类型: 算法技能
搜索
关键词: 搜索
1. 什么是搜索?
搜索分深度优先搜索与广度优先搜索。
搜索是通过进行递归操作(dfs)或者通过队列(bfs)的特殊性质来进行的一种算法,在解决题目的过程中可以通过题目来选择不同的解法。
2.深度优先搜索
深度优先搜索是通过递归来实现的一种搜索,由于他是通过不断试错的方式找到答案,所以也称“不撞南墙不回头”。
就像是这样:
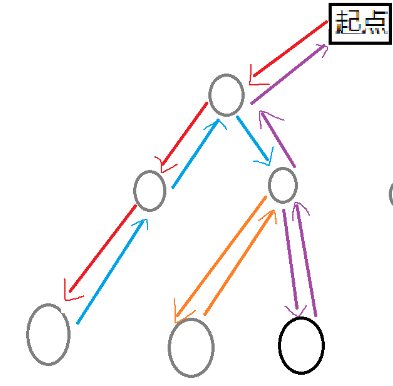
这是在深搜一个树。红色线路最先走,走到最底下以后再往回走(蓝色线路),往回走的这一步简称回溯。随后一直重复这种方式。
2.1 例题1
深搜经典例题“全排列”。
小圌的全排列
题目ID:7081
题目描述:
请你帮小圌编写一个程序,使用递归的方法,按从小到大的顺序输出 1~n 的全排列。
输入格式:
一行,一个数字 n (1≤n≤9) 。
输出格式:
按字典序从小到大的顺序输出 1~n 的全排列,每行一个排列,同一行之间数字用一个空格隔开。
输入样例:
3
输出样例:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
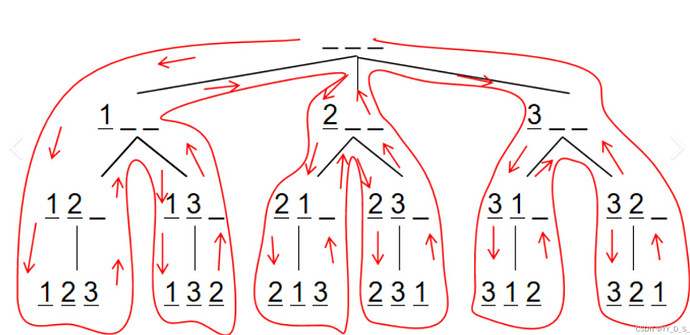
经典例题,我们来模拟一个树:
可以看到,回去的一步就是回溯
那怎么模拟这个树呢?
首先,最开始想的应该是循环,比如枚举三个数
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
n=3;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
for(int k=1;k<=n;k++){
if(i!=j&&j!=k&&i!=k){
cout<<i<<" "<<j<<" "<<k;
}
}
}
}
return 0;
}
答案:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
很明显,再枚举下去(9重?)是要超时的!
所以此时我们写深搜:
我们知道,x就是目前的位置
对于新手小白来说,先写一个输出是最好的选择:
if(x>n){
for(int i=1;i<=n;i++){
cout<<a[i]<<" ";
}
cout<<endl;
}
好家伙,输出有了,a[i]没有赋值啊!
那怎么办呢?????
此时,我们知道,需要一个分支else了,来赋值a数组。
接下来,else里写啥?
首先,要赋值,循环肯定得有:
for(int i=1;i<=n;i++){
}
里面写啥?
这时,我们发现,每个数不能重复!所以,我们需要一个vis数组!
也就是说,vis[i]=0代表没有这个数呢,vis[i]=1代表有这个数了!!
所以,我们在这里写的第一个东西:
for(int i=1;i<=n;i++){
if(vis[i]!=1){
}
}
那么,既然我们签约了这个数,那肯定要让vis数组知道,我用他了,所以我们加一句:
for(int i=1;i<=n;i++){
if(vis[i]!=1){
vis[i]=1;
}
}
那么,既然我们已经选了,所以该把a数组搞一下了!
for(int i=1;i<=n;i++){
if(vis[i]!=1){
vis[i]=1;
a[x]=i;//由于我们现在做到x这个地方了
}
}
万事俱备,只剩深搜!
那我们下一步要做目前位置的下一步,也就是x+1:
for(int i=1;i<=n;i++){
if(vis[i]!=1){
vis[i]=1;
a[x]=i;
dfs(x+1);
}
}
走完流程后,我们vis数组要派上作用,因为我们已经深搜完了,所以这个数也就没用过了(回溯),那么vis[i]=0
for(int i=1;i<=n;i++){
if(vis[i]!=1){
vis[i]=1;
a[x]=i;
dfs(x+1);
vis[i]=0;
}
}
两部分合并一下:
if(x>n){
for(int i=1;i<=n;i++){
cout<<a[i]<<" ";
}
cout<<endl;
return;
}else{
for(int i=1;i<=n;i++){
if(vis[i]!=1){
vis[i]=1;
a[x]=i;
dfs(x+1);
vis[i]=0;
}
}
}
这就是dfs了!
主函数怎么写?
我们知道,最开始从位置1开始,所以也就是:dfs(1)!
提交一下吧!
![]()
2.2 例题2
走迷宫
题目ID:1226
描述
给定一个迷宫。在迷宫中有一些障碍物无法通过,请计算出从左上角到右下角的移动方案总数。(一个位置不能经过两次,只能上下左右四个方向走)
输入格式
第一行包含两个整数n,m,表示迷宫的大小。1 <= N,M<= 6
接下来的n行,每行包含m个字符,代表迷宫。
#代表障碍
*代表你可以去的位置
左上角和右下角用“*”表示
输出格式
一个整数。
样本输入1
5 6 *****# #### #### #### ******
样本输出1
2
样本输入2
6 6 ****** ****** ****** ****** ****** ******
示例输出2
1262816
这是一道经典题目,根据上题的推导,这道题很容易想出,如果x,y代表现在的位置,那么只要x==n,y==m,就可以ans++。
如果不是位置一样,怎么写呢?
用for循环枚举四个方向,然后看那个位置有没有超出边界或是障碍物。随后,就可以用vis数组标记,dfs,最后回溯。
整个过程非常简单,而最开始的位置是dfs(1,1)。
dfs代码:
void dfs(int x,int y){
if(x==n&&y==m){
ans++;
return;
}
for(int i=0;i<4;i++){
int nx=x+dx[i];
int ny=y+dy[i];
if(nx<1||nx>n||ny<1||ny>m||mp[nx][ny]=='#'||vis[nx][ny]==1){
continue;
}
vis[nx][ny]=1;
dfs(nx,ny);
vis[nx][ny]=0;
}
}
3. 广度优先搜索
广度优先搜索是通过队列来实现的一种搜索。
就像这样:
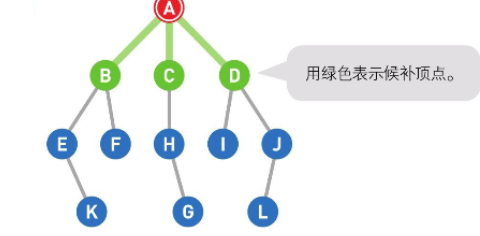
每一步都要找下一步能到哪里,进入队列,直到找到答案。
3.1 例题1
恐怖电梯
题目ID:9430
题目描述
很久很久以前,某国发生了一件怪事,很多人无缘无故失踪了,警察发现他们失踪前都乘坐过同一部电梯。
经调查,这部电梯到每一层楼都可以停,但奇怪的是,第 i 层楼 (1≤i≤N) 上有一个数字 K_i(0≤ K_i ≤N) ,电梯里只有两个按钮:“上”,“下”,上下的层数等于当前楼层上的那个数字。
当然,如果不能满足要求,相应的按钮就会失灵。例如:3, 3 ,1 ,2 ,5 代表了 K_i(K_1=3,K_2=3,…) 。在 1 楼,按“上”可以到 4 楼,按“下”是不起作用的,因为没有 −2 楼。
为了一查究竟,大胆的你决定亲自去乘坐,你想知道从 A 楼到 B 楼至少要按几次按钮呢?注意,如果不能到达,那么你可能会是下一个失踪人口。。。
输入格式:
第一行为 3 个用空格隔开的正整数,表示 N,A,B (1≤N≤200, 1≤A,B≤N) 。
第二行为 N 个用空格隔开的非负整数,表示 K_i 。
输出格式:
一个整数,即最少按键次数;若无法到达,则输出 −1。
样例输入:
5 1 5
3 3 1 2 5
样例输出:
3
这道题每一步都有两种下一步的可能,如果将当前位置的值定为 f ,那么下一步的位置有可能是 f-K_i 和 f+K_i 。
我们定义一个结构体,结构体里有这几个值 :目前的位置,已经走了几步。
那我们来广搜吧!
首先,我们之前说过,广搜是要用到队列的,所以肯定要将最开始位置入队。也就是q.push(node{s,0});(s是最开始楼层)
随后,我们要一直循环直到有答案为止。所以,我们用while循环,while(!q.empty())。
随后,根据我们前面推导过的,定义一个node f=q.front();,随后我们只要每一步都加进去下一步可能位置q.push(node{f.level+a[f.level],f.step+1});与q.push(node{f.level-a[f.level],f.step+1});
当然,vis数组肯定得有,不然卡循环了怎么办?
if(f.level<1||f.level>n||vis[f.level]) continue; vis[f.level];
最后,组装成完美的bfs代码:
queue<node> q;
int bfs(){
q.push(node{s,0});
while(!q.empty()){
node f=q.front();
q.pop();//注意,我们每次用完这个q.front后要把它扔掉
if(f.level==e) return f.step;
if(f.level<1||f.level>n||vis[f.level]) continue;
vis[f.level];
q.push(node{f.level+a[f.level],f.step+1});
q.push(node{f.level-a[f.level],f.step+1});
}
return -1;
}
3.2 例题2
相约KFC
题目ID:15703
题目描述
暑假即将到来,鱼大大和羊大大计划吃肯德基。他们在计划中在某一天选择了某一个肯德基吃午饭。
到了约定的日子,鱼大大和羊大大都是9点出发,向KFC前进,问他们两能否在中午12点之前到达约定的KFC?如果可以,那么他们最少花费多少分钟就能在KFC相约?
约定:
时间计算:起点到终点的距离为时间,即走1单位的距离,鱼大大和羊大大都要花费1分钟的时间。
‘@’ 是鱼大大的位置,‘#’ 是障碍,‘F’ 表示KFC,‘&’ 表示羊大大的位置。
‘.’,‘F’,‘@’ 和 ‘&’,这些位置都可以通过。
输入格式
第一行包含两个整数 n 和 m。
接下来的 n 行,每行输入 m 个字符来表示地图。(1 ≤ n ≤ m ≤ 200)
输出格式
如果能找到一条可行的路径并在在12点之前到达KFC,输出花费的最少时间,否则输出 “Meeting cancelled”(两人无法在12点之前相约在此KFC)。
样例
Input 1
4 4
@.#.
....
.#..
F..&
Output 1
3
这道题,一眼看去,是一道迷宫问题。
既然有迷宫,那我们先用深搜写一遍?
首先,由于深搜复杂度 $O(2^n)$,所以大概数据范围是 20~25。来看一眼…样例… 200的是包过不去的!!!
但是,秉承着TLE试错的原则,我们先来试一试(如果考试时真的不会写广搜了,深搜骗点分也是可以滴)
这里我太懒就不写了,来看一位同学的dfsTLE代码:
void dfs(int x,int y,int g1,int g2,int l,int v){
if(x==g1&&y==g2){
if(o[v]>l){
o[v]=l;
}
return;
}
for(int i=0;i<4;i++){
int s1=dx[i]+x,s2=dy[i]+y;
if(s1<n&&s1>=0&&s2<m&&s2>=0&&h[s1][s2]==false&&s[s1][s2]!='#'){
h[s1][s2]=true;
dfs(s1,s2,g1,g2,l+1,v);
h[s1][s2]=false;
}
}
}
所以,这时bfs就出来了!
其实道理是一模一样的,先将起点入队(@的位置),随后将起点标记(非常的简单),然后,与深搜相同,上代码先:
while(!q.empty()){
node f=q.front();
q.pop();
if(f.x==ex&&f.y==ey) return f.step;//如果到达KFC
for(int i=0;i<4;i++){
int dx=f.x+nx[i];
int dy=f.y+ny[i];//根据方向数组定下一步
if(dx<1||dx>n||dy<1||dy>m||vis[dx][dy]==1||c[dx][dy]=='#'){//如果下一个位置根本不存在
continue;
}
vis[dx][dy]=1;//否则标记+bfs,注意这里不用回溯
q.push({dx,dy,f.step+1});
}
}
4.<重点> 连通块问题
4.1 什么是连通块问题?
连通块问题是一种题目类别,不同于搜索、二分、贪心等的算法,它是基于搜索而创建的一种题目类别。
连通块问题具体是指在地图中,共有多少个连通的模块,比如:
#***
##**
*#
**##
这里有2个模块,分别是上面的那三个#和下面的那三个#。
来看一题例题:
4.2 例题
八连通
题目ID:1227
题目描述:
八向连通(八连通)区域指的是从区域内每一像素出发,可通过八个方向,即上、下、左、右、左上、右上、左下、右下这八个方向的移动的组合,在不越出区域的前提下,到达区域内的任意象素。
给你一个n*m的字符矩阵,一共有两种字符,求矩阵中有几个W的八连通。
输入格式:
输入一行,包含两个整数n,mn,m.
接下来nn行每行mm个字符。
输出格式:
输出一个整数。
样例输入:
10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.
样例输出:
3
约定:
1 <=n ,m<=100
这一题我们主要讲解DFS连通块问题的思路。
我们先看样例,那3个块都在哪里?
很明显,第一个块在上端,
W.....
.WWW..
....WW
第二个块在右面,
WW.
WWW
WW.
WW.
W..
W..
WW.
.W.
.W.
.W.
第三个在下部,
..W..
.W.W.
W.W.W
.W.W.
..W..
样例分析完毕,我们现在想思路。
很容易想到,我们可以从一个 'W’开始,随后向八方找,如果找到了那么标记,随后从那个点再往下走…,如果没路了再回溯。如果全都去不了了,回到最开始了,那么接着找没被标记的‘W’,以此类推。
dfs代码(方向数组):
int ax[]={1,-1,0,0,-1,1,-1,1};
int ay[]={0,0,-1,1,1,-1,-1,1};
void dfs(int x,int y){
for(int i=0;i<8;i++){
int dx=x+ax[i];
int dy=y+ay[i];//找下一个可能位置
if(dx<1||dy<1||dx>n||dy>m||mp[dx][dy]=='.'||vis[dx][dy]==1){//如果找到的地方并不是‘W’或出界或已标记
continue;
}
vis[dx][dy]=1;//标记
dfs(dx,dy);//继续
//为什么回溯不需要vis[dx][dy]=0?
//因为就算回溯了,但是标记的点依然可以走到,并不是标记的点回溯后走不到了,所以不用把标记清掉
}
}
当然,还有多种变形题,大家可以去尝试。
5.剪枝
5.1 可行性剪枝
我们目前最常使用的就是可行性剪枝,也就是对当前状态进行检查,如果当前条件不合法就不再继续,直接返回。
5.2 最优性剪枝
最优性剪枝是指从最优化的角度考虑剪枝:如果当前计算的答案已经没有之前的答案优,再计算下去一定不会更优,可以直接终止这次的搜索,考虑其他计算。
5.3 排除等效冗余
排除等效冗余人如其名,也就是说如果有一个东西,正着反着都一样,那你肯定选择一种,不会选两种,对吧? 排除等效冗余跟上面的例子就差不多。
比如,你使用两个数字1 2,来凑2,那么第一次你尝试1+2,是错误的,那2+1就肯定不对,不用再试了。
5.4 优化搜索顺序
有的时候,变换搜索的顺序可能会起到不一般的效果。
在一些题目中,可以通过对子问题分支进行分析,先解决相对简单的子问题从而使尚未解决的子问题得到简化,通过对搜索顺序的优化可以实现这一点。
例题
小木棍
题目ID:7997
题目描述:
乔治有一些同样长的小木棍,他把这些木棍随意砍成几段,直到每段的长都不超过 50 。现在,他想把小木棍拼接成原来的样子,但是却忘记了自己开始时有多少根木棍和它们的长度。给出每段小木棍的长度,编程帮他找出原始木棍的最小可能长度。
输入格式:
第一行为一个单独的整数 N 表示砍过以后的小木棍的总数。 第二行为 N 个用空格隔开的正整数,表示 N 根小木棍的长度。(1≤N≤65)
输出格式:
输出仅一行,表示要求的原始木棍的最小可能长度。
样例输入:
9 5 2 1 5 2 1 5 2 1
样例输出:
6
这道题就是一道经典的排除等效冗余。
我们发现,木棍4 5的拼接和木棍5 4的拼接都是一样的,我们就不需要重复计算了。这就是一种排除等效冗余(当然,还有很多种)
这是我们的思路:
1.枚举原始木棍长度
2.计算出原始木棍根数(分组组数)
3.dfs 判断是否可以组合出这么多根这么长的原始木棍
而且,我们可以发现,如果先用短木棍,那么需要很多根连续的短木棍接上一根长木棍才能拼成一根原来的长棍,那么短木棍都用了后,剩下了大量长木棍,拼起来就不如短木棍灵活,更难接出原始长度。
而先用长木棍,最后再用短木棍,这样就剩下了相对较短的木棍,能更加灵活地拼接出原始长度。
这样我们又多了一种思路~
我们还发现, 如果原始长度不能被所有木棍的长度之和整除的话 ,那么绝对不行,这种情况就continue了。
写出dfs代码:
void dfs(int tot,int last,int rest){
if(rest==0){ //当前原始木棍拼完
if(tot==duan){//有足够的原始木棍
//输出,结束程序
}
//找到下一没有使用的最长的木棍
dfs(tot+1,/*当前位置*/,chang-a[/*下一个*/])
}
//找第一个木棍长度小于等于rest 的位置
for(int i=/*第一个位置*/;i<=cnt;i++){
dfs(tot,i,rest-a[i]);
}
}
例题
质数肋骨
题目ID:8719
题目描述
农民约翰的母牛总是生产出最好的肋骨。你能通过农民约翰和美国农业部标记在每根肋骨上的数字认出它们。农民约翰确定他卖给买方的是真正的质数肋骨,是因为从右边开始切下肋骨,每次还剩下的肋骨上的数字都组成一个质数,举例来说: 7 3 3 1 全部肋骨上的数字 7331是质数;三根肋骨 733是质数;二根肋骨 73 是质数;当然,最后一根肋骨 7 也是质数。7331 被叫做长度 4 的特殊质数。
输入格式
写一个程序对给定的肋骨的数目 N(1≤N≤8), 求出所有的特殊质数。数字1不被看作一个质数。
输出格式
按顺序输出长度为 N 的特殊质数,每行一个。
样例
Input 1
4
Output 1
2333
2339
2393
2399
2939
3119
3137
3733
3739
3793
3797
5939
7193
7331
7333
7393
样例解释
无
首先,我们发现数据样例为 N小于等于 8,看着还行啊…
看题,要减掉尾部的数,且必须是质数。判断质数NlogN,再加上八位数,包超时的啊!
剪枝,也就是我们可以将尾数是0,2,4,5,6,8的数直接PASS掉,将第一位是0,4,6,8,9的直接PASS掉(因为最后只剩下首位了,必须是质数),最后就完事了!
代码:
int a[10]={2,3,5,7}; //首位的数
int b[10]={1,3,7,9}; //后面可能的数
void dfs(int x, int num){
if(x==n){
cout<<num<<endl;
return ;
}
for(int i=0;i<4;i++){
int t=num*10+b[i];
if(is_prime(t)){//判断质数
dfs(x+1,t); //回溯
}
}
}
6. 记忆化(搜索)
6.1 什么是记忆化搜索?
当算法需要计算某个子问题的结果时,它首先检查是否已经计算过该问题。如果已经计算过,则直接返回已经存储的结果。否则,计算该问题,并将结果存储下来备用。
6.2 引入例题
爬楼梯
题目ID:9243
题目描述
一段楼梯有n级台阶。你每次可以跨一个、两个或者三个台阶。
请问走上n级台阶有几种方案?答案对998244353取模。
输入格式
一行一个数n。
输出格式
一行一个数,表示方案数。
样例
Input 1
3
Output 1
4
样例解释
1 + 1 + 1 = 3
1 + 2 = 3
2 + 1 = 3
3 = 3
数据范围
n≤1000
对于这道题目,很多人可以想到递推, 递推算法是一种用若干步可重复运算来描述复杂问题的方法 。那我们可以给出递推公式:a[i]=(a[i-1]%mod+a[i-2]%mod+a[i-3]%mod)%mod;
递推确实可以得出正确答案,关键代码如下:
a[1]=1;
a[2]=2;
a[3]=4;
for(int i=4;i<=n;i++){
a[i]=(a[i-1]%mod+a[i-2]%mod+a[i-3]%mod)%mod;
}
当然,我们也可以写递归:
int f(int x){
if(x==1) return 1;
if(x==2) return 2;
if(x==3) return 4;
else return f(x-1)+f(x-2)+f(x-3);
}
这些和记忆化有什么关系呢?
我们发现,递推和递归其实都是需要记住答案才能往下推进,这为我们有了引入,来看例题:
6.3 例题
数塔问题
题目ID:3657
题目描述
数字三角形。如下所示为一个数字三角形。请编一个程序计算从顶到底的某处的一条路径,使该路径所经过的数字总和最大。只要求输出总和。
1、 一步可向下或右斜线向下走;
2、 三角形行数小于等于100;
3、 三角形中的数字为0,1,…,99;
测试数据通过键盘逐行输入,如上例数据应以如下所示格式输入:
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
在这个例子中,路径应该是7−>3−>8−>7−>5,总和是30
输入格式:
第一行输入一个整数N,表示数塔高度
接下去N行,第i行有i个整数
输出格式:
一个整数
样例输入:
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
样例输出:
30
这道题就是一道记忆化搜索的经典题目了。
我们发现,这道题很像贪心但不是贪心,如样例:
贪心:7->8->1->7->5为28
正确:7->3->8->7->5为30
很明显不对
记忆化搜索启动!
我们用f数组来记录已经走过的地方的结果,初始化为0。那这玩意到底咋写呢?
首先,我们提到过,记忆化如果记录过直接提出来用,所以:
int dfs(int i,int j){
if(f[i][j]!=0) return f[i][j];
}
如果不是?
我们先说明,我们要从下往上得出答案,所以如果i在最底层,也就是i=n,那答案是a[i][j]。
int dfs(int i,int j){
if(f[i][j]!=0) return f[i][j];
if(i==n){
f[i][j]=a[i][j];
}else{
???
}
}
如果不是怎么办?
经过推导可以得出公式:f[i][j]=a[i][j]+max(dfs(i+1,j),dfs(i+1,j+1));
而且最后答案肯定是 return f[i][j];直接给dfs:
int dfs(int i,int j){
if(f[i][j]!=0) return f[i][j];
if(i==n){
f[i][j]=a[i][j];
}else{
f[i][j]=a[i][j]+max(dfs(i+1,j),dfs(i+1,j+1));
}
return f[i][j];
}