姓名: 帅贤
赛道: 基础组
类型: 算法技能
基础算法知识概括
关键词: 基础算法&总结
(本文仅为作者看法,如有问题,倡议提出)
时光回转,流溯于基础算法间,悄然一个定格,停留在了结构体
结构体是个团结的类型,他可以把很多东西合并成一个整体进行调用,为了什么呢?比如:你需要在一个数组排序时把另一个数组也要按照原本对应情况进行跟随,如果自己去编写函数,那么不仅会很麻烦,而且还有着不稳定的风险,而使用结构体时只需要排序其中一个变量,整个结构体就会随之变化,结构体还有很多好处,很多东西都可以在输入时就完成预处理,而且跟着其中一个变量,整个结构体都会随之改变。另外补一句,有的东西有现成的就不要去自己编,不仅是繁琐的问题,有时还会严重影响到时间复杂度,形成TLE,别问为什么,问就是我干过了。
结构体格式
struct /*结构体名字,例如studebt*/{
//变量,例如age,height;
}//变量名,如x;
//cin>>x.age>>x.height;
//cout<<x.age<<" "<<x.height;
当然结构体中也是可以编写函数的。
本人就喜欢在结构体中完成输入输出。
缓缓转移视角,来到了排序
排序也是当时把我恶心的不要不要的一个东西,变化莫测,还是有点难度的。
排序的种类很多,算是个大家庭了,冒泡排序,快速排序,选择排序,插入排序,归并排序,计数排序,桶排序等等
冒泡排序
为啥加冒泡排序呢?因为他的工作原理和鱼儿吐泡泡一样,相邻的两个位置进行比较,较大的就往上浮,这样每次遍历,都能把剩下的序列中最大的数字浮上来,最后就会形成排好的序列了。
肯定会有人问,咋写?我只告诉你要两个for循环,一个if,然后你自己想。
代码思路,从第一个数开始比,比到n-(以排好序列的个数),如果浮上来的那个数比这个位置的数大,就交换,否则就不变。(交换可以使用swap函数)
快速排序
之所以叫快速排序,就是因为他的时间复杂度相对于其他排序较快,说普通点,快速排序就是sort排序,举个例子就ok了,假设你有一个无序数列a[1005],其中的1~n项被填入了数字,现在需要快速排序,那么就是这样
sort(a+1,a+n+1,cmp);
那么我写的cmp是什么呢
一个自定义的函数,从小到大就是
bool cmp(int x,int y){
return x<y;
}
从大到小就是把小于改成大于
切记,sort排序是一种不定排序,如果需要将她变成稳定排序需要加上stable_,在sort之前,向上面那个代码,像将它变成稳定排序就要这样
stable_sort(a+1,a+n+1,sort);
选择排序
就是从未排序列中找到最小的选出来,放到队首,然后是当前未排序列中最大的,移到最前面,这种排序方式就是选择排序。
选择排序是一种不定排序,并不是一种稳定排序,所以要谨慎使用。
插入排序
插入排序就是把一个记录过的数字插入到一个有序数列中,从而实现排序。
for(int i=2;i<=n;i++){
for(int j=i;j>=2;j--){
if(a[j]<a[j-1]){
swap(a[j],a[j-1]);
}
else break;
}
}
归并排序
桶排序
就是把利用数组创建很多的桶,遇到每个数字的时候就把那个数字放到对应的桶里,最后在按照所需要的顺序进行输出或者按照题目所需要的方法进行计算
计数排序
先便利这个无序的数列,让每一个整数按照值对号入座,对应数组下标的元素加1。
直接便利数组,输出数组元素的下标值,元素的值是几就输出多少次。
接下来就是贪心问题了
贪心是一种思想并不是一种有着固定格式的算法,贪心的思路就是把一个问题拆分成许多个子问题,然后得到子问题的最优解,最后将每个子问题的最优解进行合并,然后完成此题。那么什么时候需要用到贪心呢,一个很平常的问题,找钱。假设要找服务员76元钱,且要使我们给服务员的钱的张数尽量小,那我们就要先看100元,100元不能放,那就看50元,50元可以放1个,还剩26元,接下来是20元,20元可以放一个,还剩6元接下来是5元,可以放一个,还剩一元,最后是1元,可以放一个,找钱找完了,最优解是4张,这就是贪心。
随着时间的推移,接下来就是枚举了
枚举就是把本题所需要的结果的各种情况都列举出来,然后进行统一计算或者一系列操作。
枚举法很容易超时,所以只限于题目规模较小的题目
随着就是模拟
模拟是啥呢,就是按照题目的要求,实际情况来进行编写程序,顺着题目要求走,完成本题。
烦人的高精度又来了
难点充斥在了string类型的处理与进位退位的计算,不能让他只祸害我,也来祸害祸害你们。
然后就是递推了
递推说难也不难,说简单也不简单,名字很高级,放到数学中就是找规律,例如:
1 1 2 3 5 8 13……,按这个规律,输入一个n,求这个规律下去的第n位是几。
很简单,递推式就是f(n)=f(n-1)+f(n-2)
接下来,噩梦就要开始了,递归。
怎么形容递归呢,dfs是他的孩子。什么是递归?递归就是递归。什么是递归?递归就是递归……这句话看似是一句废话,实际上就相当于一个没有返回的递归。切入正题,递归其实是一种算法,什么样的算法呢,通过调用自身来解决问题,一直达到一个条件后 返回,不断不断的返回出来,有一个很好理解的例子:

那么这句话咋理解呢,先看最中间的,我的小鲤鱼,然后往外开放变成了抱着我的小鲤鱼的我,在不断的开放,其中我的小鲤鱼就是递归中的返回条件,而第一个抱着开始,就进入了递归,的我则是不断不断的一层一层的返回。最基础的递归懂了吗?
没看懂
再看一遍
看懂了
接下来,就讲讲他的儿子,dfs,深度优先搜索。
dfs分为迷宫类和棋盘类,好那么我们先讲来历。
由遍历引入:
int a[];
for(int i=1;i<=n;i++){
cout<<a[i];
}
数组是一种线性逻辑的数组结构
所以这是线性排列的遍历方法
特点:除了最后一个点以外,每一个点都以一个唯一的节点
那如果是树状的遍历呢?
我们就需要用到回溯
在之前的学习过程中,什么算法跟回溯息息相关?
递归
递归可以进入到下一层
他又可以从下一层返回
问题可以转换成规模更小的子问题
完完全全,彻彻底底,真真切切就是递归(分治)算法
来了来了,因为迷宫类我说在前面,所以我先讲棋盘类
这类题目往往都是关于棋盘的,而关于棋盘就能让人很头疼,别的其不说,就专说中国象棋好了,兵有过河不过河,马在棋盘上正常情况有八个走法,还有象,炮,俥等子的走法,有时棋盘还来个不规则(破损的棋盘),真是能让人头疼。
迷宫类
迷宫类通常是在一张或多张地图中进行提问与解答,在地图中,我们需要考虑诸多问题,例如:如何写深搜,怎么处理边界,怎么计算不该走回头路时不回头,怎么避开障碍物等等。
还有就是分治思想了,分治思想是个什么东西呢,就是把题目拆成若干子问题,找到每个问题的关系进行递归,从而合并得到结果。
时光从缝隙间流逝,二分查找来到你身边
为啥要这个二分查找,直接遍历他不香吗?不香,直接遍历而超时的栗子都吃过吧所以,二分他就来了。
这个二分咋实现呢?
很简单,首先需要一个中间值,为了最最最快速,所以中间值我采用了左端点加左端点减右端点的差除以二的方式,这个方式比左端点加右端点除以二要快一丢丢,但有事样例就卡的是这一丢丢,所以要谨慎处理。
紧紧跟着的,就是咋们的栈和队列了
这俩家伙算是同一个兄弟吧,只不过顺序不同,栈是蛮不讲理的,你先进去反而要后出来,而队列就是先来后到讲规矩的,先进的就先出来。
这俩家伙有着各式各样的函数,还有各式各样的练习题,也不是一个好惹的家伙。
小广搜也来了(bfs)
在找最短路径时,dfs就会大大增加时间复杂度,举个例子:假如终点就在起点旁边,他也会把整个地图的所有可能性全部列举出来,这样就不利于找最短路径,因此我们就需要广度优先搜索,那么广搜是个什么鬼呢?
广搜是一种图形搜索演算法。简单的说,BFS是从根节点开始,沿着树的宽度遍历树的节点,如果发现目标,则演算终止。
所谓广度优先算法,就是算法自始至终一直通过已找到和未找到顶点之间的边界向外扩展,就是说,算法首先搜索和x距离为k的所有顶点,然后再去搜索和X距离为k+l的其他顶点。
所谓广度,就是一层一层的,向下遍历,层层堵截,我们如果要是广度优先遍历的话,我们的结果是V1 V2 V3 V4 V5 V6 V7 V8。
广搜bfs适合做一些找最短路径的题
树和图也紧随其后
树就难在一些概念
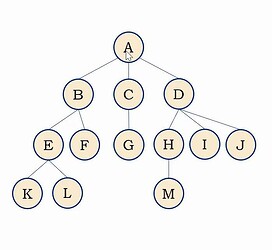
结点的度: 结点拥有的子树或者分支的个数。如A结点有三棵子树、所以A结点的度为3。
树的度: 树中各结点度的最大值。如图中结点度最大为3(A、D结点),所以树的度为3.
树的深度:(或高度):树中结点的最大层次。
树的宽度: 整棵树中某一层中最多的结点数称为树的宽度
父结点/双亲结点: 称上端结点为下端结点的父结点。
孩子结点: 称下端结点为上端结点的子节点。
兄弟结点: 称同一个父结点的多个子结点为兄弟结点
祖先结点: 又称从根结点到某个子结点所经过的所有结点称为这个结点的祖先
子孙结点: 称以某个结点为根的子树中的任意结点都是该结点的子孙
根结点: 一棵树至少有一个结点,这个结点就是根结点。
叶子结点: 又叫终端结点,指度为0的结点
非终端结点: 又叫分支结点,指度不为0的结点。都是非终端结点。除了根结点之外的非终端结点,也叫做内部结点
图也是一些概念
有向图即每条边都有方向,在有向图中,通常将边称作弧,含箭头的一端称为弧头,另一端称为弧尾,记作<Vi,Vj>,表示从顶端Vi到顶点Vj有一条边
无向图即每条边没有方向,在无向图中,通常将边称作弧,但不分弧头和弧尾,记作(Vi,Vi)表示Vi与Vj有一条边让他们相连接
在树中有一块非常重要的东西,先序遍历,中序遍历,后序遍历,恶心不在这,难在给你两个序,让你求出第三个序,并画出这棵树。
然后就是动态规划,背包问题了
动态规划是运筹学的一个分支,是求解决策过程最优化的数学方法。原理:把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解。
动态规划主要运用于背包问题中。
动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值的解。动态规划算法与分治思想(把题目拆成若干子问题,找到每个问题的关系进行递归,从而合并并得到结果。)类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样,但它们具有相同的填表格式。
基础算法到此结束,谢幕 ![]()
![]()
![]() 撒花!!!
撒花!!!