姓名: 石润禾
赛道: 提高组
类型: 算法技能
【最小生成树(MST)】
关键词: 图论、最小生成树、MST
前置知识:并查集,贪心
定义:
生成树:无向图中,一个连通图的最小连通子图称作该图的生成树(不能带环,保持连通,但边要尽可能少). 有 n 个顶点的图的生成树有 n-1 条边.
最小生成树:权值之和最小的生成树。
1.Kruskal 算法
步骤:一开始所有的点都自成一个连通分量,每次选出权值最小的边,如果这条边的两个顶点不在一个连通分量中,就把这条边加入最小生成树中,直到所有的点都在连通分量中为止。
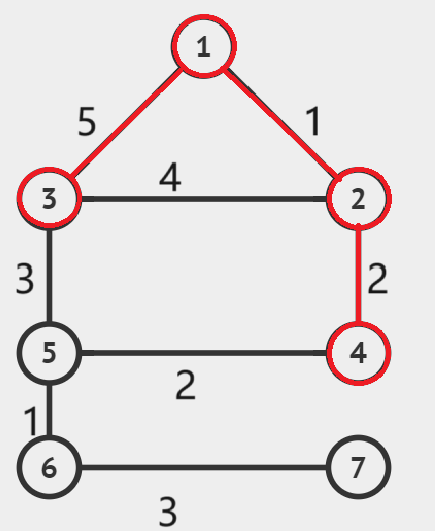
图示:
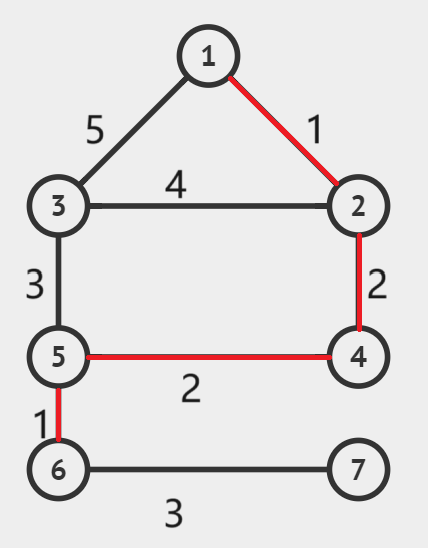
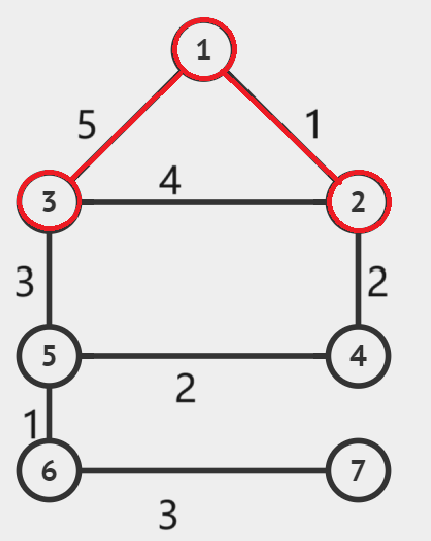
开始:
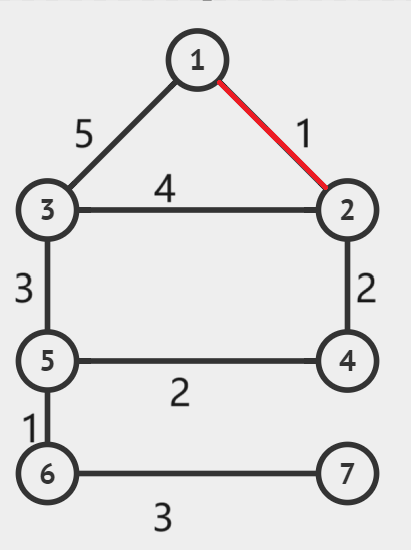
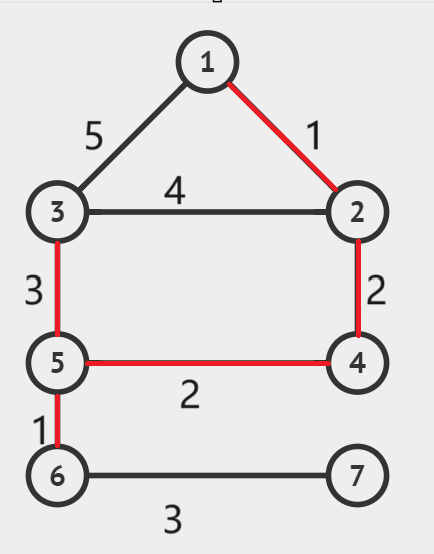
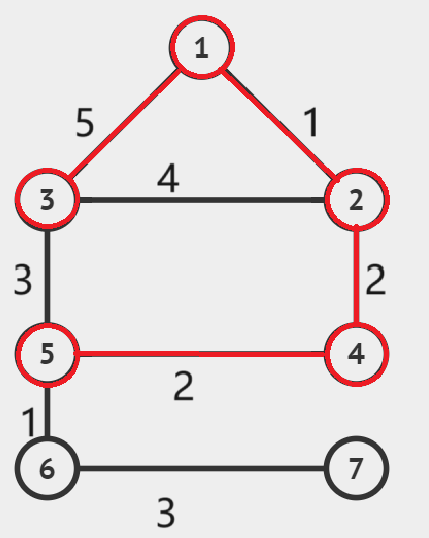
选出边权最小的边(1,2不在同一个连通分量中,将这条边加入生成树):
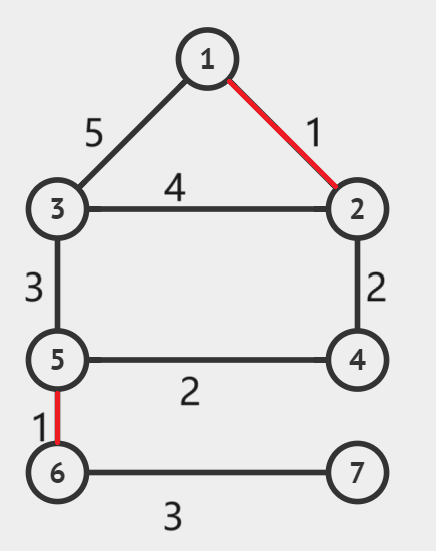
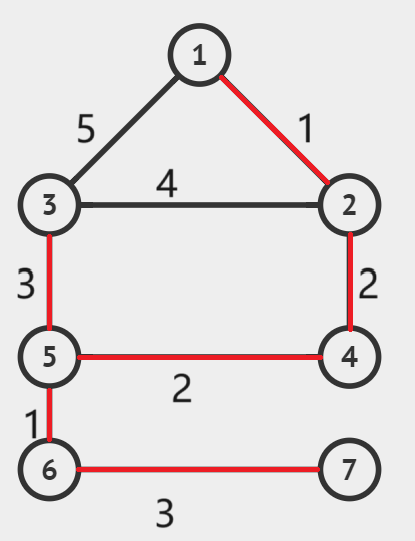
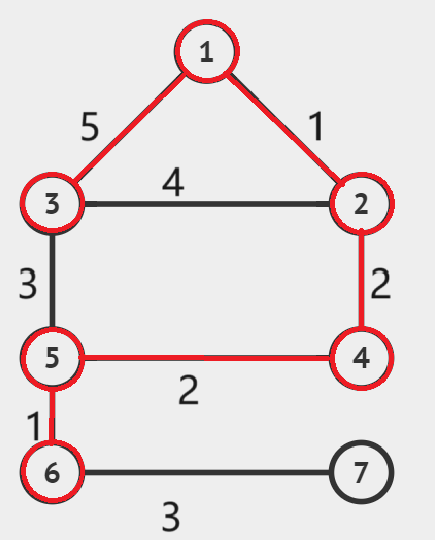
同上
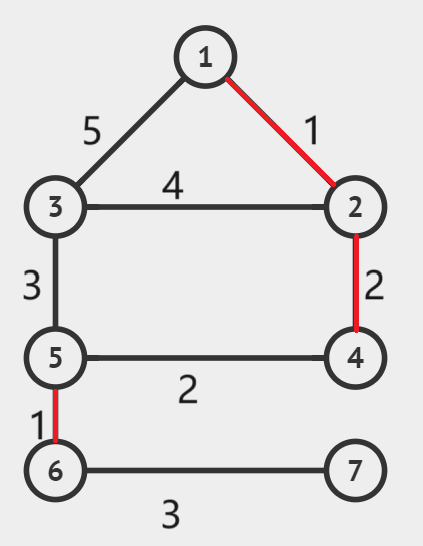
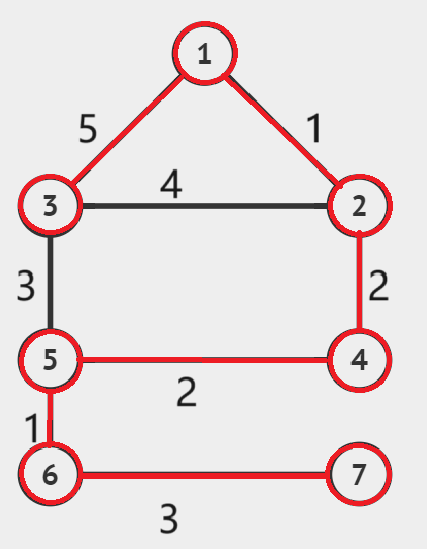
这时候我们发现所有的点都在同一个连通分量中了,所以停止操作。
核心代码:
int fa(int x)//并查集找父亲
{
if(x==f[x]) return x;
return fa(f[x]);
}
void kruskal()
{
for(int i=0;i<m;i++)//枚举每条边(已按边权排好序)
{
int a=e[i].a,b=e[i].b,w=e[i].w;
a=find(a),b=find(b);
if(a!=b)//如果这条边的两个节点不在同一个连通分量中
{
p[a]=b;//合并这两个节点
res+=w;//边权之和
cnt++;//边数量+1
}
}
}
2.Prim 算法
步骤:从图中任意一个点开始,选择与这个点相邻的边权最小的边,并将此边所连接的点加入到生成树的集合中。然后再从新加入的点出发,重复以上操作直到所有的节点都被加入到生成树中。
图示:
开始:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| 0 | inf | inf | inf | inf | inf | inf |
用1去更新2,3
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| 0 | 1 | 5 | inf | inf | inf | inf |
用2去更新4
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| 0 | 1 | 5 | 3 | inf | inf | inf |
用4去更新5
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| 0 | 1 | 5 | 3 | 5 | inf | inf |
用5去更新6
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| 0 | 1 | 5 | 3 | 5 | 6 | inf |
用6去更新7
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| 0 | 1 | 5 | 3 | 5 | 6 | 9 |
现在所有点都在生成树中,结束操作。
核心代码:
int prim(int s)
{
memset(dis,0x3f,sizeof(dis));//所有边一开始都未选,距离先设为无穷大
dis[s]=0;//起点到自己的距离为0
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> pq;
pq.push(make_pair(0,s));//起点入队
int ans=0;//权值和
while(!pq.empty())
{
int u=pq.top().second;
pq.pop();
if(vis[u]) continue;//访问过则跳过
vis[u]=1;//标记为已访问
for(int i=0;i<g[u].size();i++)
{
int v=g[u][i].first;
int w=g[u][i].second;
if(!vis[v]&&w<dis[v])
{
dis[v]=w;//更新邻接点距离
pq.push(make_pair(dis[v], v));//将邻接点入队
}
}
ans+=dis[u];//更新权值总和
}
return ans;
}
制作不易,不喜勿喷,本人蒟蒻,若有不足请多多指教哦! ![]() \; 点个赞呗~
\; 点个赞呗~![]()