姓名: 陶荣杰
赛道: 省选组
类型: 算法技能
树链剖分
关键词:重链剖分,LCA,DFS序,线段树
前置知识
线段树,DFS序,LCA
树链剖分简介
~~~~ 树链剖分是将树剖分成若干条链的形式,使它组成线性结构,以更好的维护树上路径的信息。
~~~~~ 树链剖分有多种形式,有长链剖分,重链剖分和实链剖分。而重链剖分的特征是吧“最大的”儿子称为重儿子,以此把树剖分成若干条重链。因为重链剖分应用较多,所以一般来说,「树链剖分」都指「重链剖分」。
~~~ 重链剖分是提高树上搜索效率的一个巧妙的方法。它按一定规则把树“剖分”成一条条从根节点到叶子节点的不相交的链,把对树的操作转换成对链的操作。而重链剖分可以让从根节点到任意一条链只需要经过 O(log_2n) 条链,从而使操作的复杂度为 O(log_2n) 。
~~~~ 重链剖分的特别之处就是每条链上的DFS序都是有序的,所以往往结合线段树来高效处理树上查询和修改问题。
重链剖分与LCA
~~~~ 我们来通过求最近公共祖(LCA)先来更好的介绍重链剖分的思想。
~~~~~ 求LCA的各种算法其主要原理都是快速“跳”到祖先节点,回顾一下求 LCA的两种方法:
1 . 倍增法:用二进制递增直接往祖先“跳“。
2 . Tarjan算法:用并查集合并子树,子树内的节点指向子树的根,查询LCA时可以直接从节点跳到子树的根,从而实现快速”跳“。
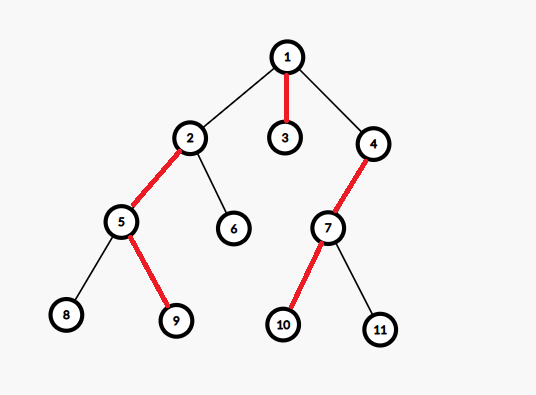
~~~~~ 重链剖分求LCA也是”跳“到祖先节点,但”跳“法比较巧妙。它把树”剖分“成从根节点到叶子节点的一条条链路,每个点都只属于一条链,链路不相交,而链上任意两个相邻的节点都为父子关系,如下图(随便剖的)。
~~~~~ 这样图中就有3条链,可以发现,相同链上两点的LCA便是深度较浅的那个点,比如LCA(4,10)=4,LCA(2,9)=2。那不在同一条链呢?那就跳到同一个链上,比如LCA(9,11),如果我们把9和11跳到同一条链上,那么就跟前面一样了。
~ ~~~ 所以如果我们让跳的链更少,也就是让链尽量少且尽量长,也就能让“剖分“更高效。
~~~~~~ 那到底要怎样”剖分“呢?注意每个节点都只能属于一条链。很自然就能想到观察树上的节点分布情况,每次选择那些有更多子节点的分支建链。链会更长一些,从而使链的数量更少。
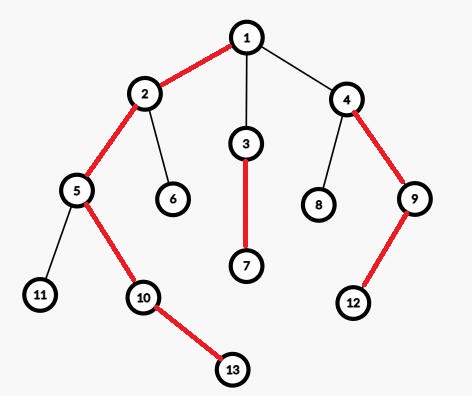
~~~~ 如下图,从1开始,每次选择些有更多子节点的分支建链,最终得到了3条链。从叶子节点到根节点1也最多经过1条链。
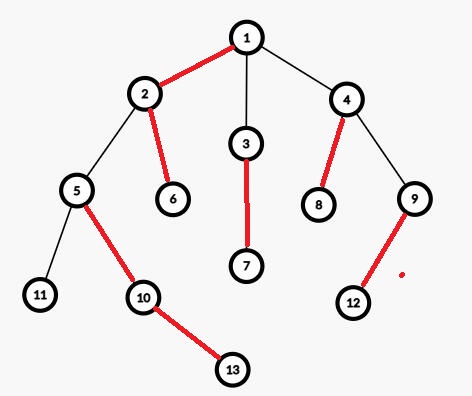
~~~~~ 例如下图,从1开始,随意建链,最终得到了5条链,而且从叶子节点到根节点1最多经过2条链,显然比上图更劣势。
~~~~~ 以上就是重链剖分的核心思想了,但在具体实现之前你还要记住以下概念:
1 . 重儿子:对于一个非叶子节点,其所有儿子中子树节点数最多(包括这个儿子)的节点。例如对于1,它的三个儿子2,3,4。子树节点数分别是6,2,4,显然2是1的重儿子。如果多个儿子中子树节点数一样,随便取其中一个就行了。
2 . 轻儿子:除了重儿子外的儿子,例如3,4就是轻儿子。
3 . 重边:父亲节点连接重儿子的边。例如(1,2),(4,9)就是重边。
4 . 重链:连续的重边而形成的链(或者说是连续的重儿子组成的链)。重链上任意两个相邻的节点都是父子关系。1,2,5,10,13就形成了一条重链。每条重链都是以轻儿子或根节点作为起点。可以把单独的一个叶子节点也看成一条重链,如11。
5 . 轻边:除了重边以外的边,任意两条重链都是用一条轻边所连接的。如(1,4)。
6 . 链头:一条重链上深度最浅的点。链头必定是个轻儿子或根节点。如果把一条重链看成一个集合,链头就是这个集合的集。与并查集类比,链头就是并查集的集。树链剖分就是通过用链头的快速跳跃实现高效操作的。1,3和4都是链头。
另外你还需知道以下的基本定义
| 变量 | 含义 |
|---|---|
| fa(x) | 表示节点 x 在树上的父亲 |
| dep(x) | 表示节点 x 在树上的深度 |
| size(x) | 表示节点 x 的子树节点个数 |
| son(x) | 表示节点 x 的重儿子 |
| top(x) | 表示节点 x 所在重链的链头 |
| id(x) | 表示节点 x 的DFS序 |
具体实现
~~~~~ 首先跑第一遍DFS求出 fa,dep,size,son 这些基本信息 。
void dfs(int u,int fa){
p[u].fa=fa;
p[u].size=1;
p[u].dep=p[fa].dep+1;
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
if(v==fa) continue;//不能是父亲
dfs(v,u);
p[u].size+=p[v].size;
if(p[u].son==0|p[v].size>p[p[u].son].size){
p[u].son=v;//重儿子
}
}
}
~~~~~ 知道这些信息还不够,所以得进行第二遍DFS来建链。
~~~~ 特别注意:需要先对重儿子进行遍历,使一条重链上的DFS序连续,这样就可以使用线段树进行链上的维护,进而可以维护一整棵树。
void dfs2(int u,int t){
p[u].id=++dfn;
p[u].top=t;
if(!p[u].son) return;//叶子节点就直接返回
dfs2(p[u].son,t);//先遍历重儿子
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
if(v==p[u].fa|v==p[u].son) continue;//不能遍历重儿子和父亲,因为已经遍历过了
dfs2(v,v);
}
}
~~~~~~ 然后再让初值按DFS序排好,便于用线段树维护。
for(int i=1;i<=n;i++){
w[p[i].id]=a[i];//对号入座
}
~~~~~ 接下来就是经典常谈(线段树)了(难崩
int ls(int p){return p<<1;}
int rs(int p){return (p<<1)+1;}
void pushup(int p){
tree[p]=tree[ls(p)]+tree[rs(p)];
}
void build(int p,int pl,int pr){
if(pl==pr){tree[p]=w[pl]%mod;return;}
int mid=(pl+pr)>>1;
build(ls(p),pl,mid);
build(rs(p),mid+1,pr);
pushup(p);
}
void add(int p,int pl,int pr,int k){
lazy[p]+=k);
tree[p]+=(pr-pl+1)*k);
}
void pushdown(int p,int pl,int pr){
if(lazy[p]){
int mid=(pl+pr)>>1;
add(ls(p),pl,mid,lazy[p]);
add(rs(p),mid+1,pr,lazy[p]);
lazy[p]=0;
}
}
void update(int p,int pl,int pr,int l,int r,int k){
if(l<=pl&&pr<=r){
add(p,pl,pr,k);
return;
}
pushdown(p,pl,pr);
int mid=(pl+pr)>>1;
if(l<=mid) update(ls(p),pl,mid,l,r,k);
if(mid<r) update(rs(p),mid+1,pr,l,r,k);
pushup(p);
}
int query(int p,int pl,int pr,int l,int r){
if(l<=pl&&pr<=r){return tree[p];}
int res=0,mid=(pl+pr)>>1;
pushdown(p,pl,pr);
if(l<=mid) res=res+query(ls(p),pl,mid,l,r);
if(mid<r) res=res+query(rs(p),mid+1,pr,l,r);
return res;
}
~~~~~ 树链剖分最经典的应用莫过于树上的最短路径修改,我们知道树上两点 的的最短路径一定经过他们的LCA,所以也是一个查找LCA的过程。我们来说下具体实现。
如果我们要求 x 与 y 的LCA。
-
x 与 y 在同一条重链上。不用说,重链上的节点都是祖先和后代的关系,设 y 的深度比 x 浅 ,那么 LCA(x, y)=y 。
-
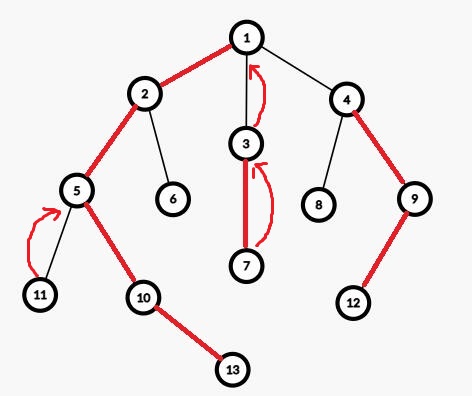
x 与 y 不在同一条重链上,设 y 所在重链链头深度比 x 所在重链链头深度浅,让 x 先跳到先跳到重链链头,然后穿过轻边到另一条重链上,重复此流程直到 x 与 y 在同一条重链上。重链的定义可以保证最后能跳到同一条重链上。例如我们要求 LCA(11,7) 。
~~~~ 11所在重链链头比较深,所以让11穿过轻边到达5。此时7所在重链链头更深,让7跳到链头再穿过轻边到达1。此时5和1在同一条重连上,LCA就为深度较浅的1了。
int lca(int x,int y){
while(p[x].top!=p[y].top){//跳到同一条链上
if(p[p[x].top].dep<p[p[y].top].dep){swap(x,y);}
x=p[p[x].top].fa;
}
if(p[x].dep<p[y].dep){swap(x,y);}
return y;
}
~~~~~ 欸,这时候聪明的人就发现了,这跳的过程不就是在走树上两点的最短路吗,那么要做树上最短路修改时可不可以边跳边修改呢,而且一条重链上的DFS序是连续的也很好修改啊。(实锤这话是作者说的
~~~~ 嘿,这树上最短路径修改还真是这样的。所以路径修改就跟求LCA差不多。这也是重链剖分一个巧妙之处。
void upd_c(int x,int y,int k){
while(p[x].top!=p[y].top){//不在同一条重链上
if(p[p[x].top].dep<p[p[y].top].dep){swap(x,y);}
update(1,1,n,p[p[x].top].id,p[x].id,k);//跳的过程中进行区间修改
x=p[p[x].top].fa;
}
if(p[x].dep<p[y].dep){swap(x,y);}
update(1,1,n,p[y].id,p[x].id,k);
}
~~~~~~ amazing!很好的修改,是我的代码旋转。
~~~~~ 查询也是大同小异,把区间修改改成区间查询就行了。
~~~~~~ 这时有些偷看了模板题的人问了,不是还有子树修改吗,你这要怎么办?(还是作者说的
~~~~~ 欸,这时候又有一个聪明的人发现,这子树中的DFS序也是连续的欸,直接做 [id[x],id[x]+size[x]-1] 的区间修改不就行了。
~~~~~ 这与其说是树链剖分的妙处,不如说是DFS序的妙处。不清楚DFS序的妙用就好好补课去吧

~~~~~~ 摘自:OI-wiki(DFS(图论) - OI Wiki (oi-wiki.org))
void upd_r(int x,int k){
update(1,1,n,p[x].id,p[x].id+p[x].size-1,k);
}
~~~~~ 子树查询就是把update换成query了,不用多说了。
锵锵!最终代码
~~~~~~ 模板题目链接:题目
#include<bits/stdc++.h>
#define int long long
const int N=114514;
using namespace std;
int head[N],cnt;
int dfn;
int n,m,rt,mod,a[N],w[N],tree[N*4],lazy[N*4];
int ls(int p){return p<<1;}
int rs(int p){return (p<<1)+1;}
struct edge{
int next,to;
}e[N*2];
void add_edge(int u,int v){
e[++cnt].to=v;
e[cnt].next=head[u];
head[u]=cnt;
}
struct node{
int size,top,son,dep,fa,id,rk;
node(){
memset(this,0,sizeof(node));
}
}p[N];
void dfs(int u,int fa){
p[u].fa=fa;
p[u].size=1;
p[u].dep=p[fa].dep+1;
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
if(v==fa) continue;//不能是父亲
dfs(v,u);
p[u].size+=p[v].size;
if(p[u].son==0|p[v].size>p[p[u].son].size){
p[u].son=v;//重儿子
}
}
}
void dfs2(int u,int t){
p[u].id=++dfn;
p[u].top=t;
if(!p[u].son) return;
dfs2(p[u].son,t);//先遍历重儿子
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
if(v==p[u].fa|v==p[u].son) continue;//重儿子和父亲已经遍历过了
dfs2(v,v);
}
}
//线段树,无需多盐
void pushup(int p){
tree[p]=(tree[ls(p)]+tree[rs(p)])%mod;
}
void build(int p,int pl,int pr){
if(pl==pr){tree[p]=w[pl]%mod;return;}
int mid=(pl+pr)>>1;
build(ls(p),pl,mid);
build(rs(p),mid+1,pr);
pushup(p);
}
void add(int p,int pl,int pr,int k){
lazy[p]=(lazy[p]+k);
tree[p]=(tree[p]+(pr-pl+1)*k)%mod;
}
void pushdown(int p,int pl,int pr){
if(lazy[p]){
int mid=(pl+pr)>>1;
add(ls(p),pl,mid,lazy[p]);
add(rs(p),mid+1,pr,lazy[p]);
lazy[p]=0;
}
}
void update(int p,int pl,int pr,int l,int r,int k){
if(l<=pl&&pr<=r){
add(p,pl,pr,k);
return;
}
pushdown(p,pl,pr);
int mid=(pl+pr)>>1;
if(l<=mid) update(ls(p),pl,mid,l,r,k);
if(mid<r) update(rs(p),mid+1,pr,l,r,k);
pushup(p);
}
int query(int p,int pl,int pr,int l,int r){
if(l<=pl&&pr<=r){return tree[p]%mod;}
int res=0,mid=(pl+pr)>>1;
pushdown(p,pl,pr);
if(l<=mid) res=res+query(ls(p),pl,mid,l,r);
if(mid<r) res=res+query(rs(p),mid+1,pr,l,r);
return res%mod;
}
void upd_c(int x,int y,int k){//路径修改
while(p[x].top!=p[y].top){
if(p[p[x].top].dep<p[p[y].top].dep){swap(x,y);}
update(1,1,n,p[p[x].top].id,p[x].id,k);
x=p[p[x].top].fa;
}
if(p[x].dep<p[y].dep){swap(x,y);}
update(1,1,n,p[y].id,p[x].id,k);
}
int que_c(int x,int y){//路径查询
int res=0;
while(p[x].top!=p[y].top){
if(p[p[x].top].dep<p[p[y].top].dep){swap(x,y);}
res=(res+query(1,1,n,p[p[x].top].id,p[x].id))%mod;
x=p[p[x].top].fa;
}
if(p[x].dep<p[y].dep) {swap(x,y);}
res=(res+query(1,1,n,p[y].id,p[x].id))%mod;
return res%mod;
}
void upd_r(int x,int k){//子树修改
update(1,1,n,p[x].id,p[x].id+p[x].size-1,k);
}
int que_r(int x){//子树查询
return query(1,1,n,p[x].id,p[x].id+p[x].size-1)%mod;
}
signed main(){
cin>>n>>m>>rt>>mod;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n-1;i++){
int x,y;
cin>>x>>y;
add_edge(x,y);
add_edge(y,x);
}
dfs(rt,rt);
dfs2(rt,rt);
for(int i=1;i<=n;i++){
w[p[i].id]=a[i];
}
build(1,1,n);
while(m--){
int op,x,y,z;
cin>>op;
if(op==1){
cin>>x>>y>>z;
upd_c(x,y,z);
}
else if(op==2){
cin>>x>>y;
cout<<que_c(x,y)<<endl;
}
else if(op==3){
cin>>x>>z;
upd_r(x,z);
}
else{
cin>>x;
cout<<que_r(x)<<endl;
}
}
return 0;
}
~~~~~ 150行啊,初学者要变成出血者了。
边权转点权
~~~~~~ 边权转点权说起来非常简单。因为树只有 n-1 条边,所以我们只直接将边权传给儿子(也就是深度较深的节点)即可,可以发现除了根节点每个节点都有权值,在实现起来也只要简单在dfs1中加一行就行了,当然你也可以研究些其他写法.
a[v]=e[i].w;//注意v不是父亲节点
~~~~~ 但因为传给了儿子,所以在做树上修改时候也要改些细节
void update_tree(int x,int y,int k){
while(p[x].top!=p[y].top){
if(p[p[x].top].dep<p[p[y].top].dep) swap(x,y);
update_add(1,1,n,p[p[x].top].id,p[x].id,k);
x=p[p[x].top].fa;
}
if(p[x].dep<p[y].dep) swap(x,y);
if(p[y].id<p[x].id) update_add(1,1,n,p[y].id++,p[x].id,k);//边是记录在儿子上的,所以只能从儿子开始改
}
~~~~~ 因为 x 是要穿过轻边的,所以循环中的修改不需要动。但外面就不能从 LCA 开始改了,因为边权记录在儿子的缘故,所以要从 LCA 的 重儿子 开始改(因为一条重链的dfs序是有序的,所以可以直接写成 LCA 的 dfs序++ )。
例题
描述
给定一棵 n 个节点的无根树,共有 m 个操作,操作分为两种:
- 将节点 a 到节点 b 的路径上的所有点(包括 a 和 b )都染成颜色 c 。
- 询问节点 a 到节点 b 的路径上的颜色段数量。
分析
~~~~~~ 因为要进行树上路径修改和查询所以第一步进行树链剖分,方便我们进行树上操作。然后就是珂朵莉树的板子了
~~~~~~ 当然写线段树也是完全没问题的,分析下题目,难点就是快速统计区间颜色段数量,可以想到分治,将每个大区间拆分成每个小区间,计算出小区间后再统计出大区间的答案,也符合线段树的思想。
具体细节
练习
月下“毛景树”
[国家集训队] 旅游
ZJOI2008 树的统计
后记
~~~~~~ 这是我第一次写这样的总结,本来还准备做一个视频或者一个动画来讲解的,但因为邻近开学,再加上一个人搞对这没什么了解,所以到最后视频没剪好,动画制作也是停滞不前(自己还是太菜了),也就是说这个还是只算个“半成品”,也不知道能不能弄好,但还是会尽力去做的。
~~~~~~ 尽管观看量没那么出众,但感悟还是挺深的。
~~~~~~ 写总结的初衷也是出于想向大家分享下自己的心得,同时对自己也算是种复习了。这篇总结就是在我自学树剖后,一时起兴写出来的。过程还是挺枯燥的,花了不少时间查资料打代码,有些例题还是请别人调出来的,但最终写出来还是满高兴的,算是值得了。后来还想加LCT的,但自己实力实在一般,写出来起码还要几个月。
~~~~~~ OIer所要行的路漫长而又艰难,自己也不见得有多少起色。但回过头来,从第一次打印出“Hello world!”到遇到种种新奇的算法和数据结构。从一个小白走到现在,经历过一次次春秋交替,一次次日月更迭,一次次跌倒,又一次次站起。虽含着泪,但这又何尝不是一场精彩的旅途,一次难忘的成长呢?
~~~~~ “路漫漫其修远兮,吾将上下而求索。”
~~~~~ 也祝大家在将要到来比赛中取得好成绩了。