姓名: 金杭东
赛道: 提高组
类型: 算法技能
关键词: 搜索
1.深度优先搜索(dfs)
深度优先搜索利用递归思想枚举各个状态,复杂度较高,一般为指数级别
深度优先搜索的具体步骤是:
1.判断到达边界(到达终点),记录答案 return
2.枚举各个决策。
3.判断决策合不合法(一般是 2 种, 1. 判断是否能走(如越界和墙) 2. 是否走过(用 vis 数组标记))
下面给出伪代码:
void dfs(int x)
{
if(/*到达边界*/)
{
//记录答案
return;
}
for(/*枚举决策*/)
{
//用变量计入新状态
if(/*新状态不能走*/) continue;
if(/*新状态走过*/) continue;
vis[/*新状态*/]=1//标记
dfs(/*新状态*/)
vis[/*新状态*/]=0//回溯
}
}
2.广度优先搜索(bfs)
广搜就是从起点开始搜索,保证每种状态只会到达一次
广搜常解决在最短路(边权为 1 )问题,因为每种状态最多经过一次,所以最先到终点就是最优的。
广度优先搜索的具体步骤是:
1.处理起点(标记起点,起点入队)
2.获取队首信息,并弹出
3.枚举各个决策。
4.判断决策合不合法(一般是 2 种, 1. 判断是否能走(如越界和墙) 2. 是否走过(用 vis 数组标记))
下面给出这类题目的伪代码:
void bfs(int x,int y)
{
queue<node>q;
//处理初始状态
while(!q.empty())
{
//获取新的点
q.pop();
if(/*到达边界*/)
{
cout<<now.ans;
return;
}
for(/*遍历所有决策*/)
{
//用变量计入新状态
if(/*新状态不能走*/) continue;
if(/*新状态走过*/) continue;
//标记新状态,很重要不然会多次搜索
//压入队列(继续搜索)
}
}
}
3.剪枝
剪枝用于 dfs ,可以优化我们代码的时间复杂度,一般分为一下几种:
1.最优性剪枝,比如你要求最短路但是你目前的 ans ≥ 目前找到的最小值直接 return;。
2.可行性剪枝,如果你发现一些状态不可能到达终点(边界)直接 return;。
3.顺序性剪枝,利用排序让搜索顺序改变,从而让搜索次数变少。
下面对于每个剪枝做个伪代码:
1. 最优性剪枝
void dfs(int x,int s)//s是目前代价
{
//ans是目前的最小答案
if(s>=ans) return;
//do something
}
2. 可行性剪枝
void dfs(int x)
{
if(/*当前状态肯定不可行*/) return;
//do something
}
3. 顺序性剪枝
bool cmp(int x,int y)
{
return x>y;
}
void dfs(int x)
{
//do something
}
int main()
{
// do some thing
sort(a+1,a+1+n,cmp);
}
4.连通块问题
连通块的概念:如果一张图(或迷宫等)的一张子图满足,任意两个点可以互相到达,并且不能继续扩展了,则这张子图就是一个连通块。
给你一张无向图,如何判断这个无向图是否联通呢?
我们可以从节点 1 开始搜索( dfs 和 bfs 都可以,用 dfs 不要回溯),用一个 vis 数组计入当前节点是否访问过,没访问过就标记并继续搜索。搜索完后如果 vis 数组全被标记过图就是连通块,否则不是连通块。
下面给出这类判断连通性题目的伪代码(这里我分别给出 dfs 和 bfs 的方法)
dfs 版:
void dfs(int x)
{
for(/*遍历下一个点*/)
{
vis[/*下一个点*/]=1;
dfs(/*下一个点*/);
}
}
int main()
{
vis[1]=1;
dfs(1);
for(int i=1;i<=n;++i)
if(!vis[i])
{
cout<<"No";
return 0;
}
cout<<"Yes";
return 0;
}
bfs 版:
void bfs()
{
queue<int>q;
vis[1]=1;
q.push(1);
while(!q.empty())
{
node now=q.front();
q.pop();
for(/*遍历下一个点*/)
{
vis[/*下一个点*/]=1;
q.push(/*下一个点*/);
}
}
}
int main()
{
bfs();
for(int i=1;i<=n;++i)
if(!vis[i])
{
cout<<"No";
return 0;
}
cout<<"Yes";
return 0;
}
还有另一类问题要你求图中的连通块个数。
我们遍历所有节点,如果 vis=0 (即找到了一个新的连通块),就以哪个节点搜索即可。
下面分别给出这类题目的 dfs 和 bfs 的伪代码:
dfs 版:
void dfs(int x)
{
for(/*遍历下一个点*/)
{
vis[/*下一个点*/]=1;
dfs(/*下一个点*/);
}
}
int main()
{
for(int i=1;i<=n;++i)
if(!vis[i])
{
ans++;
vis[i]=1;
dfs(i);
}
cout<<ans;
return 0;
}
bfs 版:
void bfs(int x)
{
queue<int>q;
vis[x]=1;
q.push(x);
while(!q.empty())
{
node now=q.front();
q.pop();
for(/*遍历下一个点*/)
{
vis[/*下一个点*/]=1;
q.push(/*下一个点*/);
}
}
}
int main()
{
for(int i=1;i<=n;++i)
if(!vis[i])
{
ans++;
vis[i]=1;
bfs(i);
}
cout<<ans;
return 0;
}
5.记忆化搜索
假如我们再求斐波那契数列(不知道的自行搜索)的第 n 项,如果直接搜索复杂度大约是 O( 2^n ) ( 这个复杂度也是非常的快 ) 。
考虑优化我们发现当 n=4 时 dfs( 2 ) 会执行 2 次,但是每次的返回值都一样,于是我们可以计入一个 dp 数组 dp_x 表示 dfs( x )的返回值,刚开始 dp 数组都是 -1 ,然后开始搜索如果 dp_x=-1 就搜索下去,并把答案就在 dp_x 里。如果 dp_x!=-1 就 return dp_x ,这样就不会有无效搜索了。
下面给出记忆化搜索的伪代码:
int dfs(int x)
{
if(dp[x]==-1)
{
dp[x]=0;
for(/*枚举下一个状态*/) dp[x]+=dfs(/*下一个状态*/);
}
return dp[x];
}
6.折半搜索(meet in the middle)
折半搜索是把要搜索的东西分成两半进行搜索,然后统计答案,复杂度通常为 O( 2^{n/2} \times 2)
折半搜索的具体步骤是:
1.搜索 1~n/2 ,用 map 数组记录每一种状态的出现次数
2.搜索 n/2+1~n ,用 ans +map_{t-s} ( t 是目标状态 s 是统计到的状态)
注意:搜索 n/2+1~n 统计答案时不一定是 ans +map_{t-s} 按照题目要求可能是 ans +map_{t/s} 或其他。
下面给出这类题目的伪代码
map<int,int>mp;
void dfs1(int x)
{
if(x==n/2+1) mp[/*统计到的状态*/]++;
//do something
}
void dfs2(int x)
{
if(x==n) ans+=mp[/*目标状态-统计到的状态*/];
//do something
}
int main()
{
//do something
dfs1(1);
dfs2(n/2+1);
cout<<ans;
return 0;
}
7.双向广搜
双向广搜时将起点和终点同时放入队列搜索。
双向广搜对比普通广搜有什么优势?
黄色为终点,红色为起点,这是普通广搜遍历的点(绿点表示)
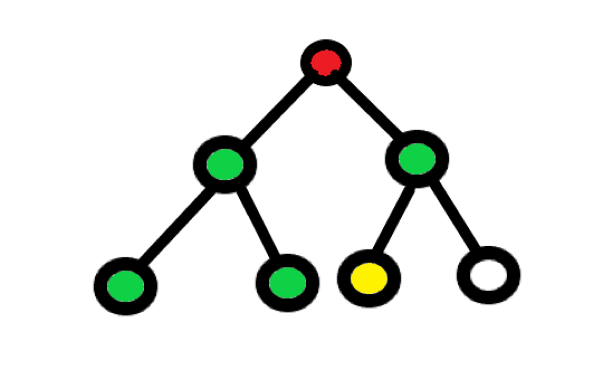
包括起点和终点是 6 个
这是双向广搜遍历的点(绿点表示)
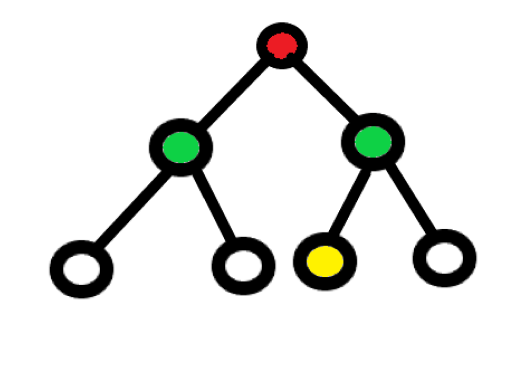
包括起点和终点是 4 个
这看似相差不大,但是你加大深度相差就大了
双向广搜具体步骤如下:
1.处理起点和终点
2.枚举状态
3.判断起点是否走到了终点走过的地方或判断终点是否走到了起点走过的地方
上个伪代码:
void bfs()
{
queue<node>q;
//处理起点和终点
while(!q.empty())
{
node now=q.front();
q.pop();
for(/*枚举状态*/)
{
if(/*满足条件*/)
{
if(/*从起点来*/) vis[/*状态*/]=1;//如果vis[/*状态*/]=2那就找到了答案
if(/*从终点来*/) vis[/*状态*/]=2;//如果vis[/*状态*/]=1那就找到了答案
}
}
}
}
怎么记录答案?
准备一个 dis 数组 dis[状态] = step ,如果找到答案就输出 dis[状态] + step 。
8.bfs与优先队列
如果 bfs 的决策权值不为 1 怎么办?
这时我们就可以用到优先队列,我们用优先队列每次取答案最小的进行搜索。
bfs+优先队列可以看做最短路算法 Dijkstra(用堆优化版)。
下面给出伪代码 :
struct node
{
long long x,ans;
bool operator<(const node &a) const
{
return a.ans<ans;
}
};
void bfs(long long x)
{
priority_queue<node>q;
//处理起点
while(!q.empty())
{
//获取队首元素并弹出
if(vis[now.x]) continue;
vis[now.x]=1;
for(int i=0;i<v[now.x].size();++i)
if(dis[v[now.x][i]]>now.ans+w[now.x][i])//当前解更优
{
//更改新节点最优解
q.push(/*新状态*/);
}
}
}
9.迭代加深搜索(IDDFS)
我们发现如果搜索的最大深度很深,而答案却在较右的深度比较浅的时候,普通搜索会让费大量的时间,这时可以用迭代加深搜索.
我们可以每次限制搜索深度,每次到达这个限制深度就结束。
那么容易发现每次搜索,都会把前面搜索过的点重新搜索一遍,这样子时间复杂度不会增加吗?
如果搜索总深度是 n ,答案深度为 k 。假如你有两种决策,普通搜索的复杂度是 O( 2^n ) ,如果使用迭代加深搜索的复杂度也就是 O(1+2^1+2^2+...+2^{k-1}+2^k)=O(2^{k+1}-1) ,可得在有两种决策时 k<n ,适合用迭代加深搜索,如果决策变多,迭代加深搜索的无效搜索可以忽略
下面给一个伪代码:
void dfs(int x,int dep)
{
if(x==dep) return;//到达限制深度
//do something
}
int main()
{
//do something
for(int i=1;i<=/*最大深度*/;++i) dfs(1,i);
return 0;
}
10.启发式搜索(A*)
启发式搜索你可以理解成是一个高级的剪枝。
启发式搜索用一个估价函数 f(i) = g(i) + h(i) ,进行剪枝
其中 g(i) 为从起点到当前状态的实际代价, h(i) 是预估从当前到终点的最小代价(也就是乐观估价)。
如果 f(i) 已经 > 当前最小答案的时候就可以return;(其实就是一个剪枝)。
h(i) 函数怎么写?
举个例子,在走迷宫中(上下左右四个方向) f(i) = g(i) + h(i) = step + mhd ( step 是走到当前点的步数, mhd 是当前点和终点的曼哈顿距离)
对于 h(i) 函数要注意:
1.h(i) 应优于实际存在的最好情况,也就是说从 i 到终点的代价要 ≤ h(i) 。
给出伪代码:
2.估价函数 h(i) 不能过于乐观,不然你的剪枝就跟没剪一样。
int h()
{
//要乐观估价(一定要 $≤$ 最小代价)
//do something
}
void dfs(int x,int s)//s是目前代价
{
//ans是目前的最小答案
if(s+h(/*传入状态*/)>=ans) return;
//do something
}
11.启发式迭代加深搜索(IDA*)
顾名思义这是迭代加深搜索(IDDFS)和启发式搜索(A*)的结合版。
也就是每次搜索用 IDDFS 来限制深度,再用 A* 算法进行剪枝。
下面还是给出伪代码:
int h()
{
//要乐观估价(一定要 $≤$ 最小代价)
//do something(估价,越准越好)
}
void dfs(int x,int s)//s是目前代价
{
//ans是目前的最小答案
if(x==dep) return;//到达限制深度return
if(s+h(/*传入状态*/)>=ans) return;
//do something
}
int main()
{
//do something
for(int i=1;i<=/*最大深度*/;++i) dfs(1,i);
return 0;
}
下面推荐一些题目
dfs: P2066,P1036,P1025,P1123。
bfs: P1746,P1135,P1126,P1141,P1602,P2658。
dfs 剪枝: P10483,P1731,P1380。
连通块问题: P1596,P1331。
记忆化搜索: P1434,P2690,P3609,P1514。
折半搜索:CF1006F。
BFS与优先队列:P1462。
IDDFS:P3052。
IDA*: P2324。