姓名: 楼逸杨
赛道: 基础组
类型: 树与图
【树与图的一点点笔记】
关键词: 树、图、树与图的例题、进制、信息编码
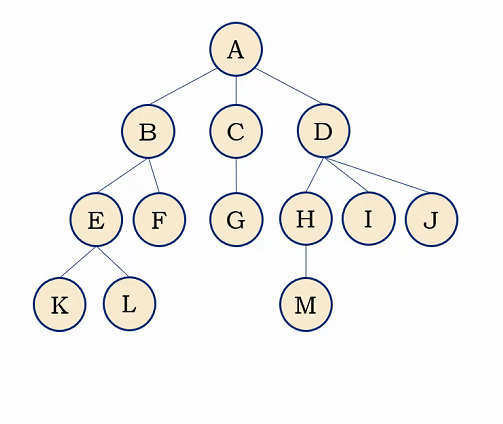
结点的度:结点拥有的子树个数或者分支的个数。如A结点有三棵子树、所以A结点的度为3
树的度:树中各结点度的最大值。如图中结点度最大为3(A、D结点),所以树的度为3。
树的深度(或高度):树中结点的最大层次。
树的宽度:整棵树中某一层中最多的结点数称为树的宽度。
根结点:一棵树至少有一个结点,这个结点就是根结点
叶子结点:又叫做终端结点,指度为0的结点。
非终端结点:又叫分支结点,指度不为0的结点,都是非终端结点。除了根结点之外的非终端结点,也叫做内部结点。
父结点/双亲结点:称上端结点为下端结点的父结点。
孩子结点:称下端结点为上端结点的子结点。
兄弟结点:称同一个父结点的多个子结点为兄弟结点。
祖先节点:又称从根节点到某个子结点所经过的所有结点称为这个结点的祖先。
子孙结点:称以某个结点为根的子树的任一结点都是该节点的子孙
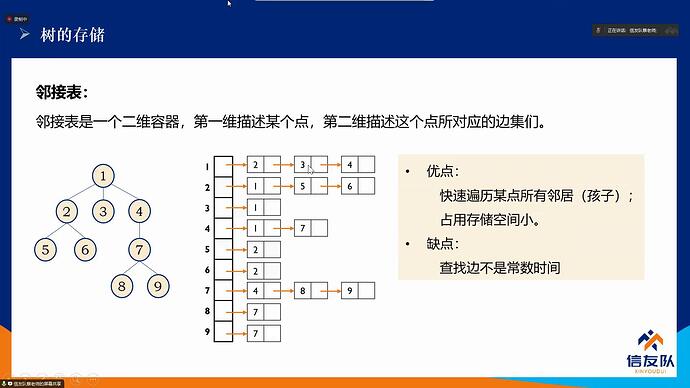
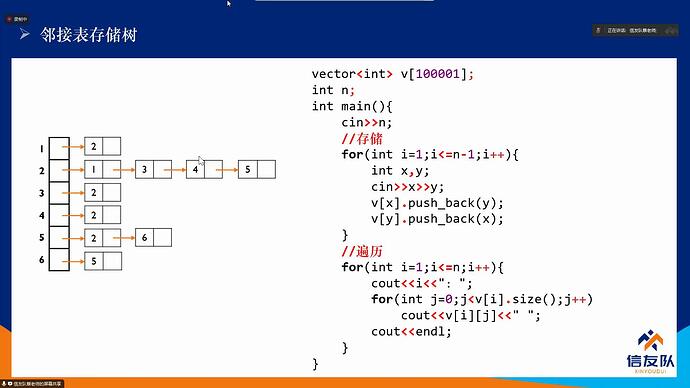
邻接表:
可以使用动态数组vector来实现,动态分配空间,随着元素的不断插入,它会按照自身的一套机制不断扩充自身的容量。
定义格式:vector<int> q;
常用函数:push_back() 在vector最后添加一个元素
empty() 判断vector是否为空(返回return时为空)
size() 返回vector数组元素个数
接下来就是我们威武的蔡老师的智慧结晶
有用就点个赞吧!!! ![]()
![]()
![]()
树的宽度
void dfs(int x,int deep){
mm[deep]++;
max_deep=max(max_deep,mm[deep]);
for(int i=1;i<=n;i++){
if(a[x][i]=='1'&&vis[i]==0){
vis[i]=1;
dfs(i,deep+1);
}
}
}
树的深度
void dfs(int x,int deep){
max_deep=max(max_deep,deep);
for(int i=1;i<=n;i++){
if(a[x][i]=='1'&&vis[i]==0){
vis[i]=1;
dfs(i,deep+1);
}
}
}
例题1
给出每一个节点的左右孩子,输出每一个节点的父亲节点,-1表示空
这题很简单,因为只有1是没有父亲结点的,其他都有
所以我们可以先初始化
int node[25]={0,-1};
再输入
for(int i=1;i<=n;i++){
int a,b;
cin>>a>>b;
if(a!=-1) node[a]=i;
if(b!=-1) node[b]=i;
}
最后输出就好了
例题2
给定一棵以 1 为根的二叉树,输出他的先序遍历,如果没有儿子为 -1
这题我们要用到函数
不断地遍历
void dfs(int k) {
if(k==-1) {
return;
}
cout<<k<<" ";
dfs(l[k]);
dfs(r[k]);
}
还要将数组内所有元素都变为-1
memset(l,-1,205);
memset(r,-1,205);
最后输入输出就可以了
例题3
现给你一棵树的所有边,请你判断若干点是否存在父子关系。此树有 n 个结点,编号 1 至 n,其中 1 号是根。
这题只要定义一个零接矩阵
用来存储就可以了
for(int i=1;i<n;i++){
int a1,a2;
cin>>a1>>a2;
a[a1][a2]=1;
}
例题4
已知一棵树,有 N 个结点,编号 1 至 N,其中 1 号是根。求树的所有叶子节点数。
这题只要判断一行中如果只有一个有关联的点就计数
for(int i=1;i<=n;i++){
int sum=0;
for(int j=1;j<=n;j++){
if(a[i][j]=='1') sum++;
}
if(sum==1&&i!=1) {
mm[ans]=i;
ans++;
cnt++;
}
}
二叉树的衍生之FBI树
这题我们要用dfs函数不断地遍历
void dfs(int l,int r){
if(l==r){//串s不再大于1
if(s[l]=='0') cout<<'B';//全0串
if(s[l]=='1') cout<<'I';//全1串
return ;
}
int mid=(l+r)/2;//中间下标
dfs(l,mid);//递归前半部分
dfs(mid+1,r);//递归后半部分
int f1=0,f2=0;//进行判断
for(int i=l;i<=r;i++){
if(s[i]=='0') f1=1;//有0的情况
if(s[i]=='1') f2=1;//有一的情况
}
if(f1==1&&f2==0) cout<<'B';//全1串
else if(f1==0&&f2==1) cout<<'I';//全0串
else cout<<'F';//有1有0的串
}
图的知识点
图是区别于线性结构(只有一个前驱和一个后驱)和树结构(一个父结点和多个子节点)的数据结构,它是一种多对多的关系。
图是由顶点集和边集组成的,通常表示为:G(V,E),其中G表示图,V表示顶点的集合,E表示边的集合。
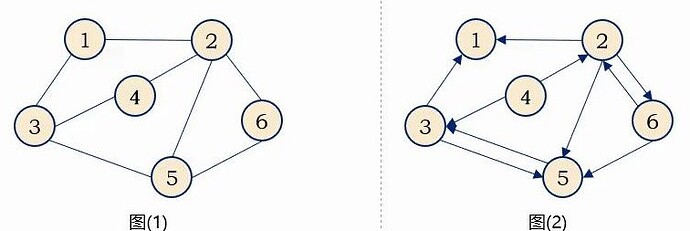
由于我无法描述下面的东西
所以用一张图片来描述
顶点的度为为以该顶点为一个端点的边的数目。
对于无向图,顶点的边数为度,度数之和是顶点边数的两倍。如图1所示:顶点V5的度为三。
对于有向图,入度是以顶点为终点,出度相反。有向图的全部顶点入度之和等于出度之和且等于边数。如图2所示:顶点V5的入度为3,出度为1。 \color{red}{(注意:入度与出度是针对有向图来说的。)}
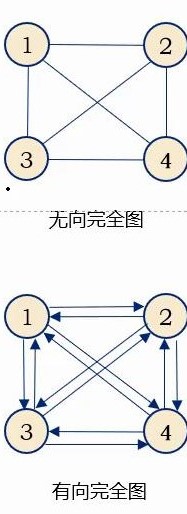
无向完全图
在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。含有n个顶点的无向完全图有 \color{red}{n(n-1)/2} 条边。
有向完全图
如果任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图。含有n个顶点的有向完全图有 \color{red}{n(n-1)} 条边。
子图
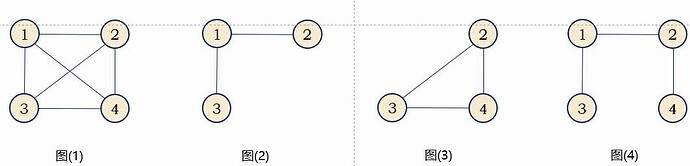
假设有两个图G=(V,{E})和G=(V‘,{E’}),如果V‘是V的子集,且E’是E的子集,则称G‘为G的子图。如图2、图3、图4、均为图1的子图
图的存储
由于本人水平过于低下只好用我们
我们威武的蔡老师的智慧结晶
连通图
在无向图G中如果从顶点V到顶点V’有路径,则称V和V‘是联通的。如果对于图中 \color{red}{任意两个顶点vi、vj ∈G,vi和vj都是联通的} ,则称G是联通图
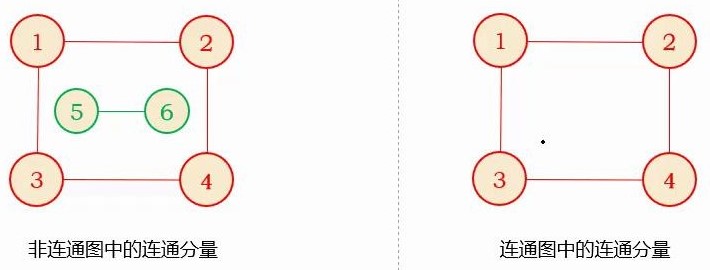
连通分量
无向图中的 \color{red}{极大连通子图} 称为 \color{red}{连通分量} ,指包含了图中尽可能多的顶点以及尽可能多的边,以至于它再加上一个点或者边之后它就不连通了
连通图的极大连通子图就是他本身。
非连通图中有多个连通分量也就是可以有多个极大连通图。
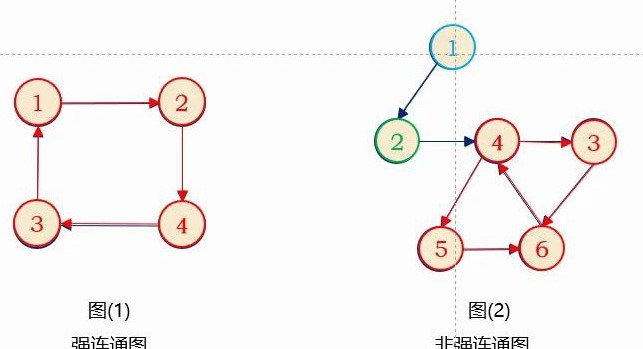
强连通图&强连通分量
在有向图G中,如果对于每一对vi、vj,vi ≠vj,从vi到vj和从vj到vi都存在路径,则称G是强连通图。
有向图中的极大强连通子图称作有向图的强连通分量。
例题1
给出一个有 n 个结点,m 条边的无向图,从 1 到 n 按顺序输出各个结点的度。
这题我们就要用到邻接矩阵来表示顶点之间的关系
首先输入
cin>>n>>m;
for(int i=1;i<=m;i++){
int a1,a2;
cin>>a1>>a2;
a[a1][a2]=1;
a[a2][a1]=1;
}
再进行遍历
for(int i=1;i<=n;i++){
int cnt=0;
for(int j=1;j<=n;j++){
if(a[i][j]==1) cnt++;
}
cout<<cnt<<'\n';
}
然后就达成了题目的要求
例题2
给出一个无向图,输出每个点相邻的那些点。
这题我们用动态数组vector就能很好的表示
先定义
vector<vector<int> >g;
再输入与初始化
g.resize(n+1);
for(int i=1;i<=m;i++){
int x,y;
cin>>x>>y;
if(x!=y){
g[x].push_back(y);
g[y].push_back(x);
}
}
再判断与输出
for(int i=1;i<=n;i++){
sort(g[i].begin(),g[i].end());
for(int j=0;j<g[i].size();j++){
if(j!=g[i].size()-1&&g[i][j]==g[i][j+1]) continue;
cout<<g[i][j]<<" ";
}
cout<<'\n';
}
例题3
给出一个无向图,和一棵树,求至少要加多少边才能将这棵树变成给定的图,如果无法变成,则输出 impossible。
这题我们只要不停的进行对比就行了,但有可能爆内存,所以可以用short
cin>>n>>m;
for(int i=1;i<=n-1;i++){
int x,y;
cin>>x>>y;
a[x][y]=1,a[y][x]=1;
}
for(int i=1;i<=m;i++){
int x,y;
cin>>x>>y;
b[x][y]=1,b[y][x]=1;
}
for(int i=1;i<=m;i++){
for(int j=1;j<=m;j++){
if(a[i][j]==0&&b[i][j]==1){
cnt++;
a[i][j]=1;
a[j][i]=1;
}
if(b[i][j]==0&&a[i][j]==1){
cout<<"impossible";
return 0;
}
}
}
cout<<cnt<<'\n';
例题4
图的dfs遍历
这题与树的dfs遍历有一点相似
所以就不讲了
dfs部分
void dfs(int x){
cout<<x<<' ';//输出顺序
for(int i=0;i<g[x].size();i++){
if(vis[g[x][i]]==1) continue;//访问数组为1,就跳过
vis[g[x][i]]=1;//不然就递归
dfs(g[x][i]);
}
}
例题5
题目描述:
给出 N 个点,M 条边的有向图,对于每个点 v,求 ()A(v) 表示从点 v 出发,能到达的编号最大的点。
这题要用bfs搜索加判断
void bfs(){
queue<int> w;
w.push(s);
while(w.size()) {
int h=w.front();
if(sum<h){//判断大小
sum=h;
}
w.pop();
for(int i=0; i<g[h].size(); i++) {
if(vis[g[h][i]]) {
continue;
}
vis[g[h][i]]=1;
w.push(g[h][i]);
}
}
}
搜索
for(int i=1;i<=n;i++){
sum=-1;
s=i;
memset(vis,0,sizeof(vis));
vis[s]=1;
bfs();
cout<<sum<<' ';
}
例题6
给出一个无向图,求图的连通分量的个数。保证无重边和自环。
这题与图的dfs遍历与连通块问题都有相似,就是他们的子问题
先进行遍历
void dfs(int x){
for(int i=0;i<g[x].size();i++){
if(vis[g[x][i]]==1) continue;
vis[g[x][i]]=1;
dfs(g[x][i]);
}
}
再进行计数
for(int i=1;i<=n;i++){
if(vis[i]==0){
cnt++;//计数器++
vis[i]=1;//访问数组为1
dfs(i);//遍历
}
}
cout<<cnt;//输出
计算机常用进制:十进制、二进制、八进制、十六进制
一、进制
进制的表达:
1.
二进制 B(binary)
八进制 O(octal)
十进制 D(decimal)
十六进制 H(hexadecimal)
或
(数值)_{(进制)}
如
(123)_{(8)}
2.编程语言表达方式
二进制 0b10或0B10
八进制 025
十进制 36
十六进制 0x1A或0X1A
进制转换
先讲位权
例如:十进制整数部分第一位的位权为1,第2位为10,第3位为100,第4位为1000……
所以R进制数的第X位的位权是X的R-1次方
按权展开法:
12345D=
110^(5-1)+210^(4-1)+310^(3-1)+410^(2-1)+510^(1-1)=
110000+21000+3100+410+51=
12345
以此类推
134.56O=
18^2+38^1+48^0+58^(-1)+6*8^(-2)=
64+24+4+0.625+0.09375=
92.71875
短除法
比如 123D转二进制
123%2=1
61%2=1
30%2=0
15%2=1
7%2=1
3%2=1
1%2=1
所以123D=1111011B
比大小
(35.565)O ?(1A.2465)H
0b11110.11 ? 01386.43
第一题
- 大于
- 小于
- 等于
- 布吉岛
第二题
- 大于
- 小于
- 等于
- 布吉岛
答案 大于 、小于
下面的代码完成了 将一个M进制的数N转换成十进制表示的式子
#include <bits/stdc++.h>
using namespace std;
int main(){
char m[1005];
int n,a[1005];
cin>>n>>m;
int len1=strlen(m);
for(int i=0;i<len1;i++){
if(m[i]>='A'&&m[i]<='F'){
a[i]=m[i]-'A'+10;
}
else a[i]=m[i]-'0';
}
int cnt=len1-1;
for(int i=0;i<len1;i++){
if(a[i]!=0) {
if(i!=0) cout<<'+'<<a[i]<<'*'<<n<<'^'<<cnt;
else cout<<a[i]<<'*'<<n<<'^'<<cnt;
}
cnt--;
}
return 0;
}
展示所用代码禁止复制,如有发现,必将追究
编码
位(bit) 最小单位
字节 (Byte,B)基本单位,每8位组成一个字节
字 2字节
单位转换
1B=8bit
1KB=2^10B=1024B
1MB=2^10KB=1024km
1GB=2^10MB=1024MB
1TB=2^10GB=1024GB
32位编译器
char :1个字节
char*(即指针变量): 4个字节(32位的寻址空间是2^32, 即32个bit,也就是4个字节。同理64位编译器)
short int : 2个字节
int: 4个字节
unsigned int : 4个字节
float: 4个字节
double: 8个字节
long: 4个字节
long long: 8个字节
unsigned long: 4个字节
64位编译器
char :1个字节
char*(即指针变量): 8个字节
short int : 2个字节
int: 4个字节
unsigned int : 4个字节
float: 4个字节
double: 8个字节
long: 8个字节
long long: 8个字节
unsigned long: 8个字节
1、机器数
一个数在计算机中的二进制表示形式,叫做这个数的机器数。机器数是带符号的,在计算机用机器数的最高位存放符号,正数为0,负数为1。
比如,十进制中的数 +3 ,计算机字长为8位,转换成二进制就是0000 0011。如果是 -3 ,就是 100 00011 。
那么,这里的 0000 0011 和 1000 0011 就是机器数。
2、机器数的真值
因为第一位是符号位,所以机器数的形式值就不等于真正的数值。
例如上面的有符号数 1000 0011,其最高位1代表负,其真正数值是 -3,而不是形式值131(1000 0011转换成十进制等于131)。所以,为区别起见,将带符号位的机器数对应的真正数值称为机器数的真值。
例:0000 0001的真值 = +000 0001 = +1,1000 0001的真值 = –000 0001 = –1
二. 原码, 反码, 补码的基础概念和计算方法
在探求为何机器要使用补码之前,让我们先了解原码、反码和补码的概念。对于一个数,计算机要使用一定的编码方式进行存储,原码、反码、补码是机器存储一个具体数字的编码方式。
三、
原码:除符号以外,前面十几就是几;符号位是0就是正数,1就是负数。
反码:正数部分和原码保持一致;负数部分,符号位置1,其他数位相反。
补码:正数部分保持相同;负数部分,在反码基础上加1;
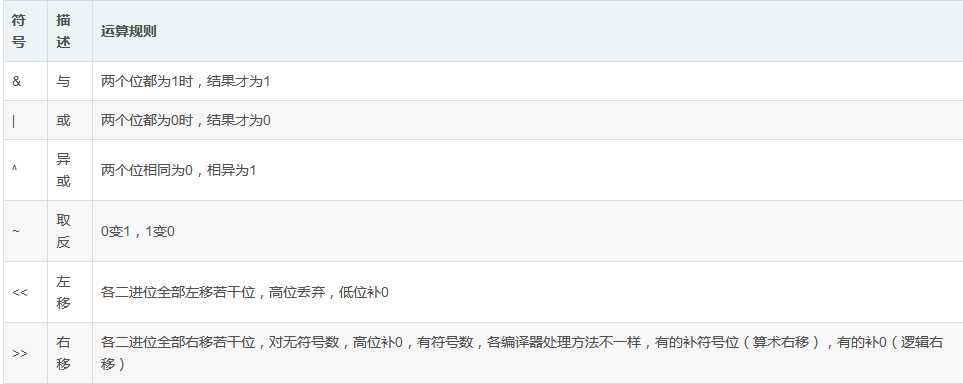
位运算
常见运用
- 按位与(&)
逻辑:对两个数的每一位进行比较,只有当两个对应的位都为1时,结果位才为1,否则为0。
用法示例:检查一个数是否同时被另外两个数整除(基于位向量的共同属性)。
int a = 12; // 二进制为 1100
int b = 15; // 二进制为 1111
int c = 3; // 二进制为 0011
// 检查a是否同时被b和c整除(即a的二进制表示中,1的位必须在b和c的对应位上也是1)
if ((a & b) == a && (a & c) == a) {
printf("a is divisible by both b and c\n");
}
- 按位或(|)
逻辑:对两个数的每一位进行比较,只要有一个对应的位为1,结果位就为1。
用法示例:合并两个数的特定位,常用于设置标志位。
int flags = 0; // 初始化为0,无标志位设置
#define FLAG1 1 // 定义标志位1
#define FLAG2 2 // 定义标志位2
// 设置标志位1
flags |= FLAG1;
// 同时设置标志位1和标志位2
flags |= FLAG2;
// 此时flags的二进制表示为 0011,表示两个标志位都被设置
- 按位异或(^)
逻辑:对两个数的每一位进行比较,如果两位相同,则结果位为0;如果不同,则结果位为1。
用法示例:无需临时变量交换两个数的值,或用于简单的加密解密操作。
int x = 5; // 二进制为 0101
int y = 9; // 二进制为 1001
// 交换x和y的值
x = x ^ y; // x变为1100 (即12)
y = x ^ y; // y变回0101 (即5),因为x现在是12,y是原来的9
x = x ^ y; // x变回1001 (即9),恢复y的值
- 按位取反(~)
逻辑:对数的每一位进行取反操作,即0变1,1变0。
注意:对于有符号整数,取反后的结果可能不是直观的“反码”,因为还涉及到符号位的扩展。
用法示例:获取一个数的反码(通常用于无符号整数或特定场景下的有符号整数操作)。
unsigned int a = 5; // 无符号整数,二进制为 0000 0101
unsigned int b = ~a; // 结果为 1111 1010,即无符号整数中的反码
- 左移(<<)
逻辑:将数的二进制表示向左移动指定的位数,右边超出的部分被丢弃,左边新增的位用0填充。
用法示例:快速乘以2的幂次方。
int a = 5; // 二进制为 0101
int b = a << 2; // 结果为 10100,即20,相当于a乘以2的2次方
- 右移(>>)
逻辑:将数的二进制表示向右移动指定的位数,右边超出的部分被丢弃。对于有符号整数,通常使用算术右移(左边用符号位填充);对于无符号整数,左边用0填充。
用法示例:快速除以2的幂次方,并保留整数部分。
int a = -8; // 二进制(补码表示)为 1111 1000(假设为32位)
int b = a >> 2; // 对于有符号整数,使用算术右移,结果为 1111 1110(即-2),相当于a除以2的2次方取整
// 对于无符号整数
unsigned int c = 16; // 二进制为 0001 0000
unsigned int d = c >> 2; // 使用逻辑右移,结果为 0000 0100,即4
1.判断整型变量奇偶
使用位运算符:&
原理
2的0次是1,2的1次是2。根据按权展开可知,只需判断最后一位即可。1的二进制是000…001。根据&运算符的特点,奇数末位是1,和1与为1,偶数则为0。
代码
//判断int类型变量奇偶
bool Judge(int n)
{
return(n&1);//奇数返回1,偶数返回0
}
2.交换变量
使用位运算符:^
原理
两个数相同,则返回0,否则,返回1。a=a^b;b=(a^b)^b=a;a=(a^b)^a=b;
代码
//交换变量 利用异或
void Change()
{
int a, b;
printf("请输入两个整数:\n");
scanf("%d %d",&a,&b);
printf("%d %d交换后为:", a, b);
a ^= b;
b ^= a;
a ^= b;
printf("%d %d\n", a, b);
}
3.乘/除2的n次
使用位运算符:<<和>> 乘用的比较多
原理
移位。不溢出的情况下,左移补0,就是乘2了。除是右移,类似,但是可能损失精度。
代码
//num乘2的n次
int Multi(int num, int n)
{
return num << n;
}
//num除2的n次
int Devide(int num, int n)
{
return num >> n;
}
4.对2的次幂取余
使用位运算符:&
原理
例如,15对8取余,15的二进制是00…01111 最多就是余7喽。8-1就是7,二进制为00…111,和00…0111相与就是余数7。
代码
//得到余数
int Yu(int num,int n)
{
int i = 1 << n;
return num&(i-1);
}
5.得到整型变量二进制形式某位置的值
原理
向右移位与1进行“&”操作,可以用来得到二进制。
//取十进制整型变量a的二进制形式的第k位
int GetWei(int n, int k)
{
int m;
m = n >> k & 1;
return m;
}
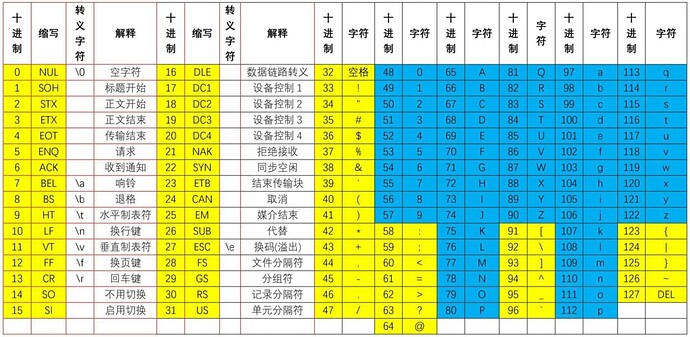
ASCII码
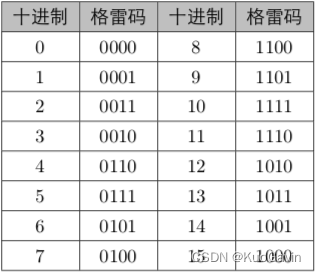
格雷码
在一组数的编码中,若任意两个相邻的代码只有一位二进制数不同,则称这种编码为格雷码(Gray Code),另外由于最大数与最小数之间也仅一位数不同,即“首尾相连”,因此又称循环码或反射码。在数字系统中,常要求代码按一定顺序变化。例如,按自然数递增计数,若采用 8421 8421 8421码,则数 0111 0111 0111变到 1000 1000 1000时四位均要变化,而在实际电路中, 4 4 4位的变化不可能绝对同时发生,则计数中可能出现短暂的其它代码( 1100 1100 1100、 1111 1111 1111等)。在特定情况下可能导致电路状态错误或输入错误。使用格雷码可以避免这种错误。格雷码有多种编码形式。
头文件C语言
#include <assert.h> //设定插入点
#include <ctype.h> //字符处理
#include <errno.h> //定义错误码
#include <float.h> //浮点数处理
#include <iso646.h> //对应各种运算符的宏
#include <limits.h> //定义各种数据类型最值的常量
#include <locale.h> //定义本地化C函数
#include <math.h> //定义数学函数
#include <setjmp.h> //异常处理支持
#include <signal.h> //信号机制支持
#include <stdarg.h> //不定参数列表支持
#include <stddef.h> //常用常量
#include <stdio.h> //定义输入/输出函数
#include <stdlib.h> //定义杂项函数及内存分配函数
#include <string.h> //字符串处理
#include <time.h> //定义关于时间的函数
#include <wchar.h> //宽字符处理及输入/输出
#include <wctype.h> //宽字符分类
头文件c++
#include <algorithm> //STL 通用算法
#include <bitset> //STL 位集容器
#include <cctype> //字符处理
#include <cerrno> //定义错误码
#include <cfloat> //浮点数处理
#include <ciso646> //对应各种运算符的宏
#include <climits> //定义各种数据类型最值的常量
#include <clocale> //定义本地化函数
#include <cmath> //定义数学函数
#include <complex> //复数类
#include <csignal> //信号机制支持
#include <csetjmp> //异常处理支持
#include <cstdarg> //不定参数列表支持
#include <cstddef> //常用常量
#include <cstdio> //定义输入/输出函数
#include <cstdlib> //定义杂项函数及内存分配函数
#include <cstring> //字符串处理
#include <ctime> //定义关于时间的函数
#include <cwchar> //宽字符处理及输入/输出
#include <cwctype> //宽字符分类
#include <deque> //STL 双端队列容器
#include <exception> //异常处理类
#include <fstream> //文件输入/输出
#include <functional> //STL 定义运算函数(代替运算符)
#include <limits> //定义各种数据类型最值常量
#include <list> //STL 线性列表容器
#include <locale> //本地化特定信息
#include <map> //STL 映射容器
#include <memory> //STL通过分配器进行的内存分配
#include<new> //动态内存分配
#include <numeric> //STL常用的数字操作
#include <iomanip> //参数化输入/输出
#include <ios> //基本输入/输出支持
#include <iosfwd> //输入/输出系统使用的前置声明
#include <iostream> //数据流输入/输出
#include <istream> //基本输入流
#include <iterator> //STL迭代器
#include <ostream> //基本输出流
#include <queue> //STL 队列容器
#include <set> //STL 集合容器
#include <sstream> //基于字符串的流
#include <stack> //STL 堆栈容器
#include <stdexcept> //标准异常类
#include <streambuf> //底层输入/输出支持
#include <string> //字符串类
#include <typeinfo> //运行期间类型信息
#include <utility> //STL 通用模板类
#include <valarray> //对包含值的数组的操作
#include <vector> //STL 动态数组容器