这题怎么写
题目描述:
我们可以把由“0”和“1”组成的字符串分为三类:全“0”串称为B串,全“1”串称为I串,既含“0”又含“1”的串则称为F串。
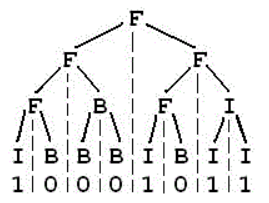
FBI树是一种二叉树,它的结点类型也包括F结点,B结点和I结点三种。由一个长度为2^N的“01”串S可以构造出一棵FBI树T,递归的构造方法如下:
-
T的根结点为R,其类型与串S的类型相同;
-
若串S的长度大于1,将串S从中间分开,分为等长的左右子串S1和S2;由左子串S1构造R的左子树T1,由右子串S2构造R的右子树T2。
现在给定一个长度为2^N的“01”串,请用上述构造方法构造出一棵FBI树,并输出它的后序遍历序列。
输入格式:
第一行是一个整数 (0≤N≤10),第二行是一个长度为 2^N 的“01”串。
输出格式:
包括一行,这一行只包含一个字符串,即FBI树的后序遍历序列。
样例输入:
3
10001011
样例输出:
IBFBBBFIBFIIIFF
提示:
我的代码
#include<bits/stdc++.h>
using namespace std;
string s;
int n;
void dfs(int l,int r){
if(l==r){
if(s[l]=='0') cout<<'B';
if(s[l]=='1') cout<<'I';
return ;
}
int mid=(l+r)/2;
dfs(l,mid);
dfs(mid+1,r);
int f1=0,f2=0;
for(int i=1;i<=r;i++){
if(s[i]=='0') f1=1;
if(s[i]=='1') f2=1;
}
if(f1==1&&f2==0) cout<<'B';
else if(f1==0&&f2==1) cout<<'I';
else cout<<'F';
}
int main() {
cin>>n>>s;
int len=pow(2,n);
dfs(0,len-1);
return 0;
}