更好的阅读: 最短路问题 - 洛谷专栏 (luogu.com.cn)
最短路问题
常见的用于解决最短路问题的算法:
BFS , Bellman-Ford , SPFA , Floyd , Dijkstra
BFS
求最小的步数,利用BFS广搜的特性,我们可以认为第一次到达某个点时的步数是最小的,
如果一个图的边权刚好可以等价于步数,则可以使用BFS解决(即边权为 1 ,或者全部相等)
时间复杂度: O(n)
void bfs(int start){
memset(dp,0x3f,sizeof dp);
queue<int>q;
q.push(start);
dis[start]=0;
while(!q.empty()){
int now=q.front();
q.pop();
for(int i=0;i<G[now].size();++i){
int v=G[now][i];
if(dis[v]==INF){
dis[v]=dis[now]+1;
q.push(v);
}
}
}
}
Bellman-Ford
if(dis[v]>dis[u]+w){
//松弛,用于更新v的最短路
}
我们可以发现,在一个图中,任意一个点的最短路径长度最多被更新 n-1 次(因为一个点的最短路一定来源于其他点)
for(int T=0;T<n;++T){
for(int i=0;i<m;++i){
int u=E[i].u;
int v=E[i].v;
int w=E[i].w;
dis[v]=min(dis[v],dis[u]+w);
}
}
时间复杂度: O(mn)
SPFA
用BFS方式实现的Bellman-Ford
void spfa(int start){
memset(dp,0x3f,sizeof dp);
queue<int>q;
q.push(start);
dis[start]=0;
while(!q.empty()){
int now=q.front();
q.pop();
for(int i=0;i<G[now].size();++i){
int v=G[now][i];
if(dis[v]>dis[now]+w){
dis[v]=dis[now]+w;
q.push(v);
}
}
}
}
时间复杂度:一般情况下是 O(kn) ,极端情况 O(nm)
可以处理负边权,也可以处理负环(死循环)
利用死循环+Bellman-Ford,那么只要有任意一个点被更新 >n-1 次的时候,我们就可以认为出现了负环
用一个数组 cnt[i] 来记录 i 的入队次数,如果 cnt[i]>n-1 则说明出现了负环
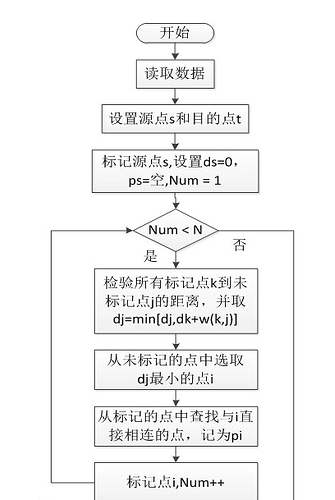
Dijkstra
核心是一个贪心,思路和Prim
Dijstra认为最短路径是越来越长的,所以当前能够达到最短路最小的点,一定不会在变小了
- 每轮选择未被标记点中最小的点 now
- 将它进行标记,并更新 now 周围的 dis[v]=min(dis[v],dis[now]+w)
- 重复 1\sim 2 ,直到所有点被标记( n 轮)
typedef pair<int,int>PII;
void Dijkstra(int start){
prority_queue<PII,vecter<PII>,greater<PII> >q;
memset(dis,0x3f,sizeof dis);
dis[start]=0;
q.push(make_pair(0,start));
for(int T=0;T<n;++T){
PII now=q.top();
q.pop();
int id=now.second;
vis[id]=1;
vis[now]=1;
for(int i=0;i<G[now].size();++i){
int v=G[id].v;
int w=G[id].w;
if(dis[v]>dis[id]+w){
dis[v]=dis[id]+w;
q.push(make_pair(dis[v],v));
}
}
}
}
时间复杂度: O(n^2+m)
可以使用优先队列优化找点的过程: O(nlogn)
不能处理负边权,也不能处理负环
Floyd
多源最短路径算法,能够处理任意点对的最短路长度
计算出一个矩阵 G[i][j] 表示 i 到 j 的最短路径长度
核心思想是动态规划
- 状态 G[i][j] 表示用过前 k 个点的情况下 i 到 j 的最短路径
- 转移方程:选择 k 作为中间节点更新 G[i][j]=min(G[i[j],G[i][k]+G[k][j]])
- 初始化:根据题目需求初始化,赋值边即可
- 答案:任意点对最短路为 G[i][j]
for(int k=1;k<=n;++k){
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
G[i][j]=min(G[i][j],G[i][k]+G[k][j]);
}
}
}
时间复杂度: O(n^3)
能处理负边权,不能处理负环
图论问题中主要考虑几个细节:
- 负边权
- 负环->没有最短路
- 重边
- 不连通
- 自环
| 名称 | 时间复杂度 | 约束 | 类型 |
|---|---|---|---|
| BFS | O(n) | 边权必须相等 | 单源最短路径算法 |
| Bellman-Ford | O(mn) | 能处理负边权,不能处理负环 | 单源最短路径算法 |
| SPFA | O(kn)\sim O(nm) | 能处理负边权和负环 | 单源最短路径算法 |
| Dijkstra | O(n^2) 优化后 O(nlogn) | 不能处理负边权和负环 | 单源最短路径算法 |
| Floyd | O(n^3) | 能处理负边权,不能处理负环 | 多源最短路径算法 |